Pythonで標準化、分散、偏差値を求めるなど

#!/usr/bin/env python
# coding: utf-8

# In[3]:


import pandas as pd
df = pd.read_csv("../../data/hensachi.csv")


# In[4]:


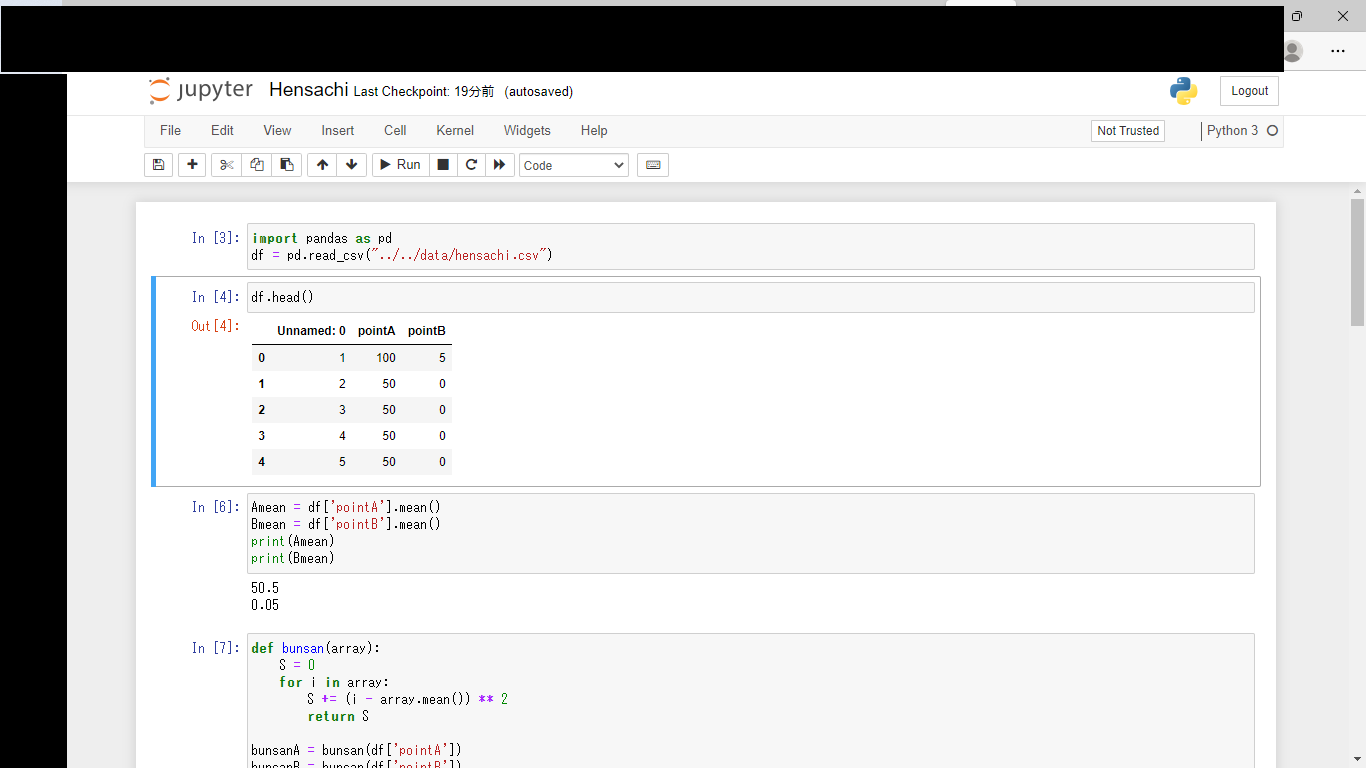
df.head()


# In[6]:


Amean = df['pointA'].mean()
Bmean = df['pointB'].mean()
print(Amean)
print(Bmean)


# In[7]:


def bunsan(array):
	""" データの配列から分散を求める """
    S = 0
    for i in array:
        S += (i - array.mean()) ** 2
        return S
    
bunsanA = bunsan(df['pointA'])
bunsanB = bunsan(df['pointB'])

hyoujyunhensaA = bunsanA ** 1/2
hyoujyunhensaB = bunsanB ** 1/2

print(bunsanA)
print(bunsanB)
print(hyoujyunhensaA)
print(hyoujyunhensaB)

        


# In[9]:


# 標準化

def standardize(array):
	""" 標準化を行う """
    s = bunsan(array) ** 1/2
    result = [(i - array.mean()) / s for i in array]
    return result

stanA = standardize(df['pointA'])
stanB = standardize(df['pointB'])

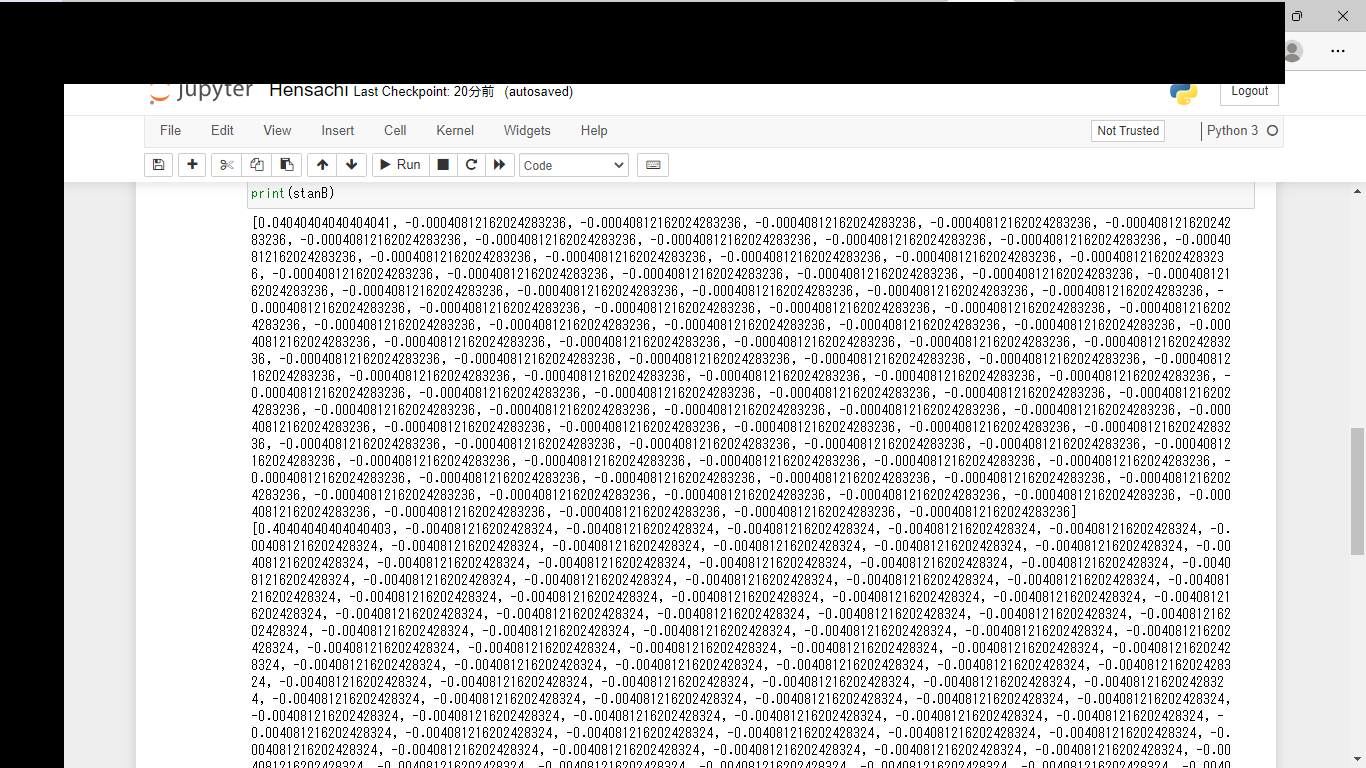
print(stanA)
print(stanB)


# In[10]:


# 偏差値
def deviation(array):
	""" 偏差値を求める """
    return [i * 10 + 50 for i in array]

hensachiA = deviation(stanA)
hensachiB = deviation(stanB)

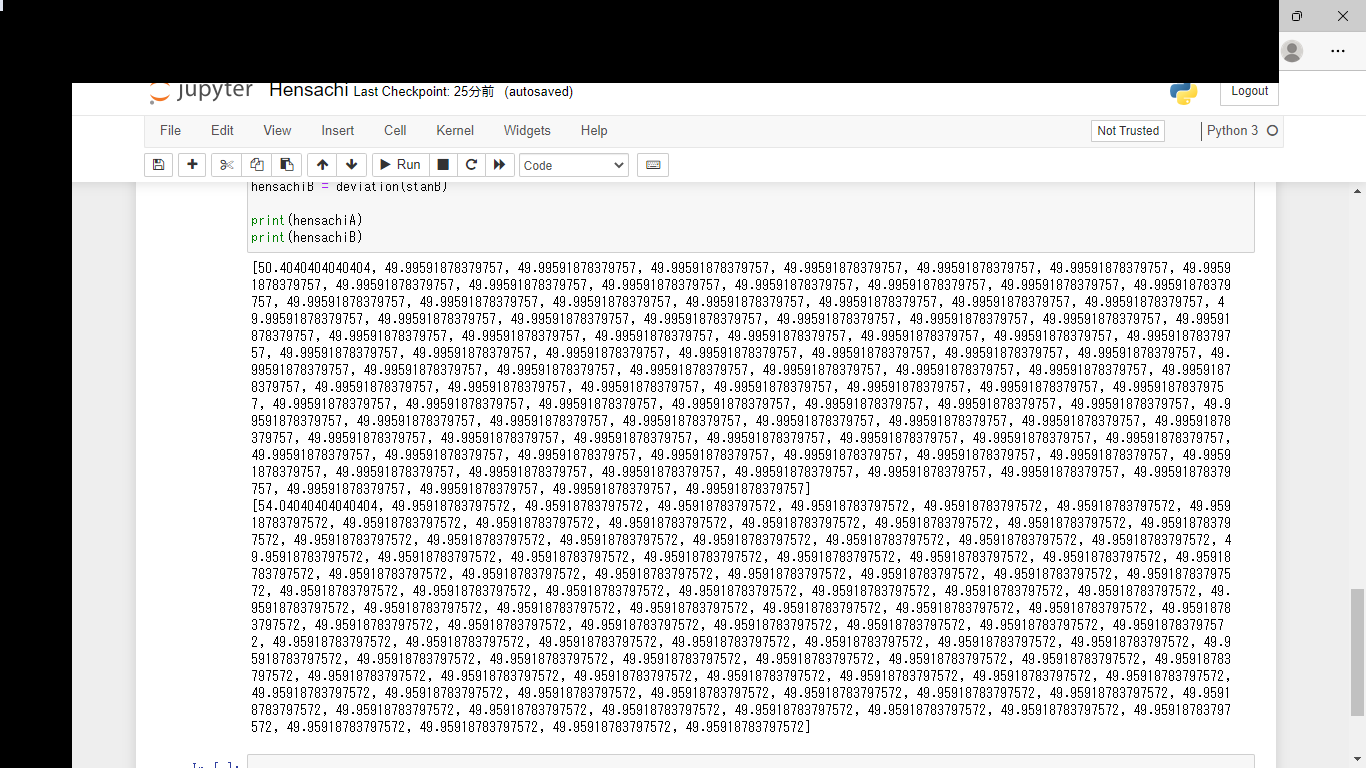
print(hensachiA)
print(hensachiB)


# In[ ]:

　Twitterで、「100人のうち、99人が50点で自分だけ100点の場合と、99人が0点で自分だけ5点の場合について、どちらが自分の偏差値が高くなるか」というツイートがあったそうなので、このようなデータで分析してみました。

　公式に当てはめて関数を作ってみたところ、このような結果になりました。

　すみません、これは偏差値ではなくて、標準化した値ですね。偏差値はこれに10倍して50を足します。

　はい、私の方がはるかに偏差値高いですね。30くらいは上ですね。当然ですね。
　分かりづらいですが、どちらも自分の偏差値が50.4040404040....となっています。

まとめ

・僕の方が偏差値が高い