概要
アルゴリズムを使ってある数までの素数を見つけ出し、配列に詰め込んでいくコードです。
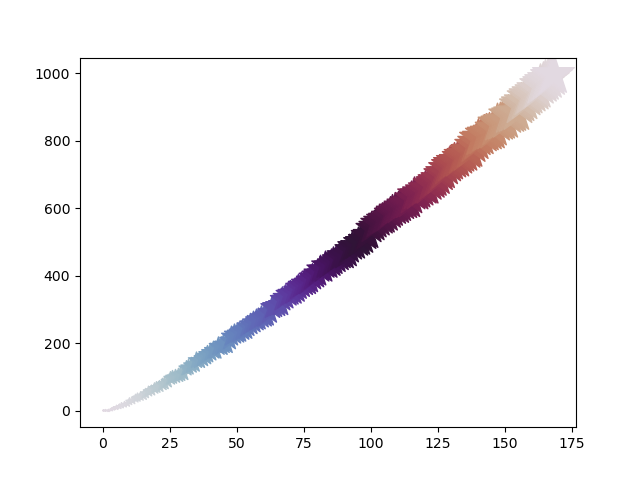
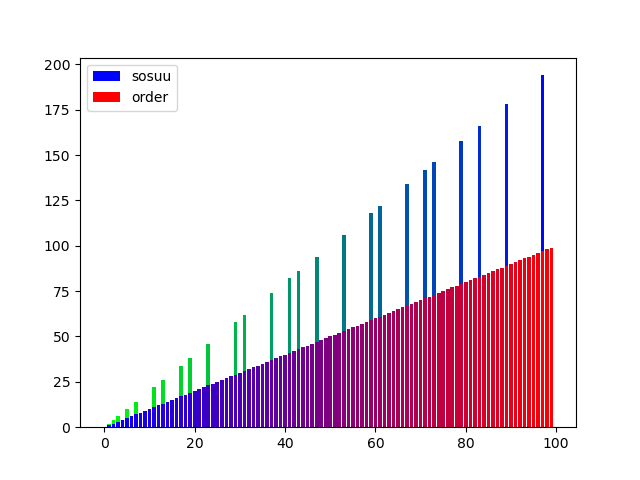
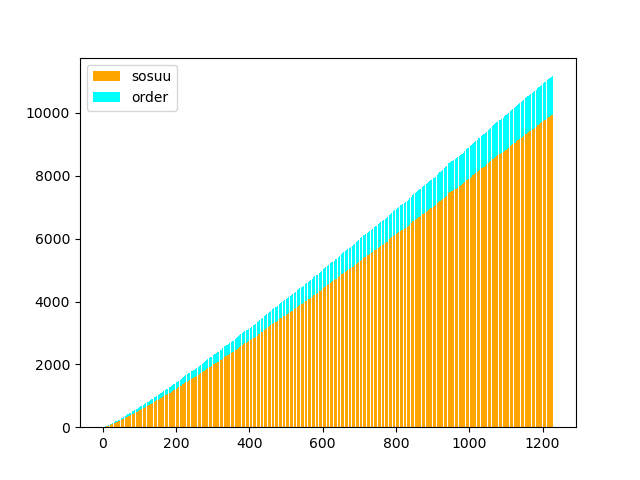
ついでに素数をグラフにして可視化しました。
from numpy import linspace
import numpy as np
import matplotlib.pyplot as plt
import random
N = 1000
def factor(N):
x = 2
insuu = []
sosuu = 0
while x <= N ** 0.5:
if N % x == 0:
insuu.append(x)
else:
pass
x += 1
# print(insuu)
if insuu == []:
sosuu = N
if sosuu != 0:
return sosuu
else:
return 0
x = range(0, N)
y = []
for i in x:
if factor(i) != 0:
y.append(factor(i))
#print(y)
#else:
#y.append(0)
#random.shuffle(y)
print(y)
for n in range(0, len(y)):
color1 = [n/N, 0.0, 1-n/N]
color2 = [1-n/N, n/N, 0.0]
#print(n)
#print(y[n])
#plt.scatter(n, y[n], s=y[n], c=y[n], vmin=0, vmax=N, cmap='cool', marker="*", edgecolors="orange")
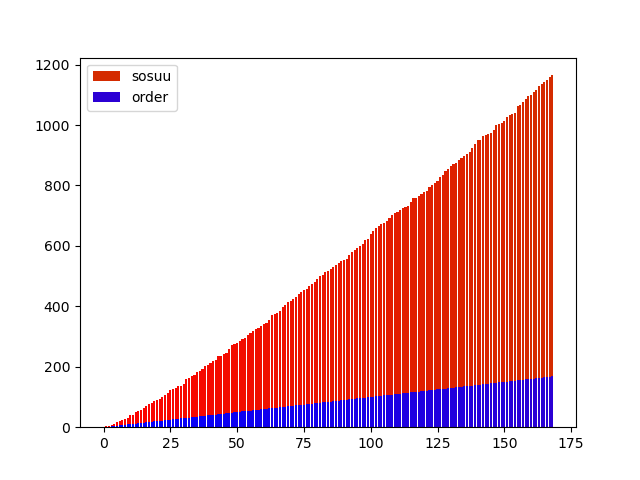
p1 = plt.bar(n,y[n], bottom=n, color=color2)
p2 = plt.bar(n,n, color=color1)
plt.legend((p1[0],p2[0]),("sosuu","order"))
plt.show()
#plt.colorbar()
print('----------------------------------------------')
def sosuuFibonacci(array):
num = 0
sosuuFibonacci = []
for i in range(0, len(array)-1):
#sosuuFibonacci.append(array[i]+array[i+1])
num += array[i]
sosuuFibonacci.append(num)
return sosuuFibonacci
y2 = sosuuFibonacci(y)
print(y2)
for n in range(0, len(y2)):
color1 = [n/N, 0.0, 1-n/N]
color2 = [1-n/N, n/N, 0.0]
#print(n)
#print(y[n])
#plt.scatter(n, y[n], s=y[n], c=y[n], vmin=0, vmax=N, cmap='cool', marker="*", edgecolors="orange")
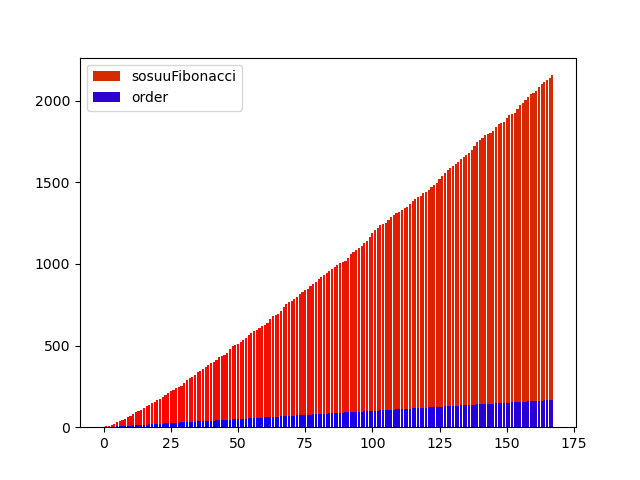
p1 = plt.bar(n,y2[n], bottom=n, color=color2)
p2 = plt.bar(n,n, color=color1)
plt.legend((p1[0],p2[0]),("sosuuFibonacci","order"))
plt.show()
#plt.colorbar()
コメントアウトしている部分は、デバッグ用の出力や、グラフなどの設定を変えたいとき用のものです。
素数を使って色々なグラフが書けましたが、素数はしょせん素数で、あまり面白みのないグラフになりました。素数がどのくらいの割合で分布しているかなどは分かりやすいと思います。
ついでに、フィボナッチ数列のように、各素数について、次の素数と足した数を配列にしたり、それまでの素数の和を配列にしたりしてみました。何か法則性を見つけたら、数学者を目指してください。あと私に教えてください。ちなみに、各素数とその次の素数の和は、5以外偶数なような気がします。あと、何故か6の倍数が67%程入っていました。
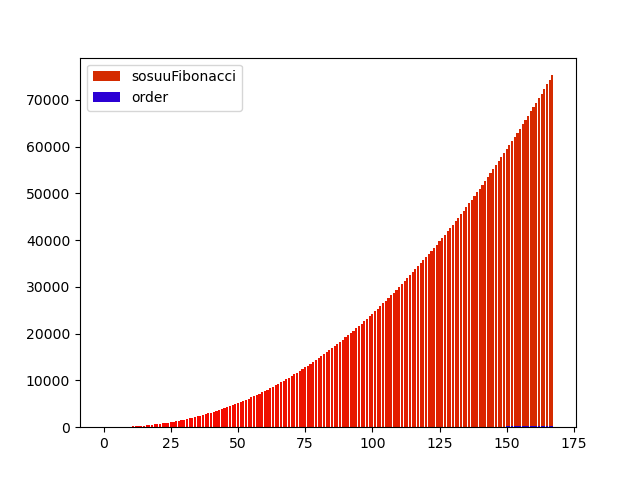
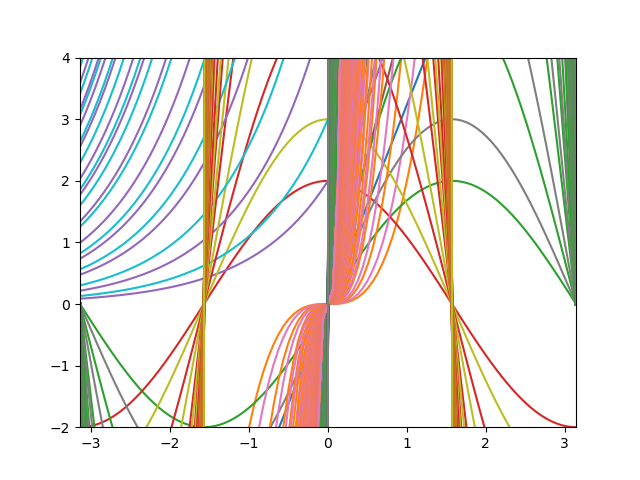
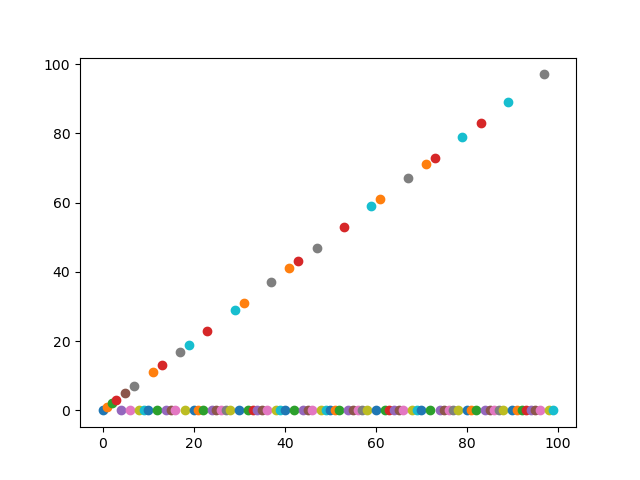
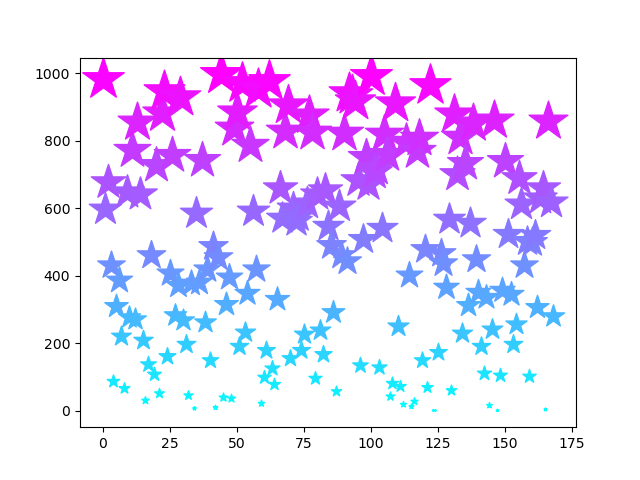
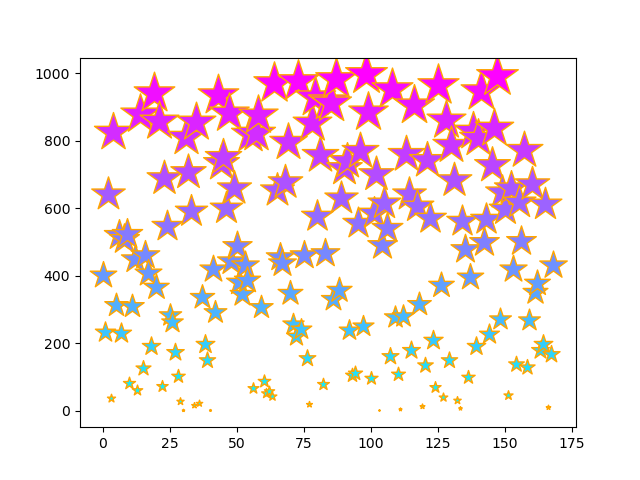
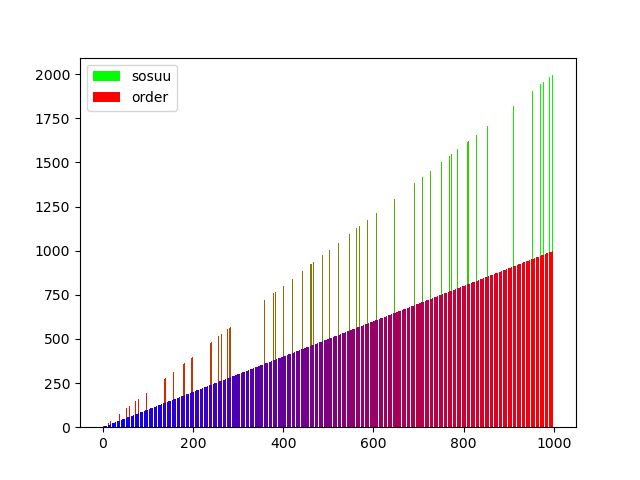
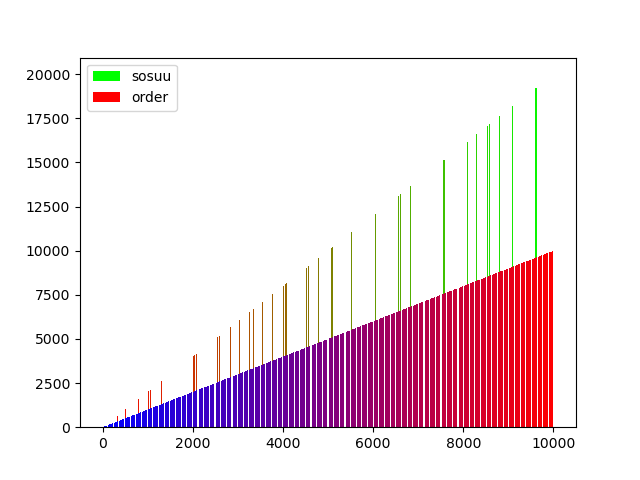
グラフはこんな感じになりました
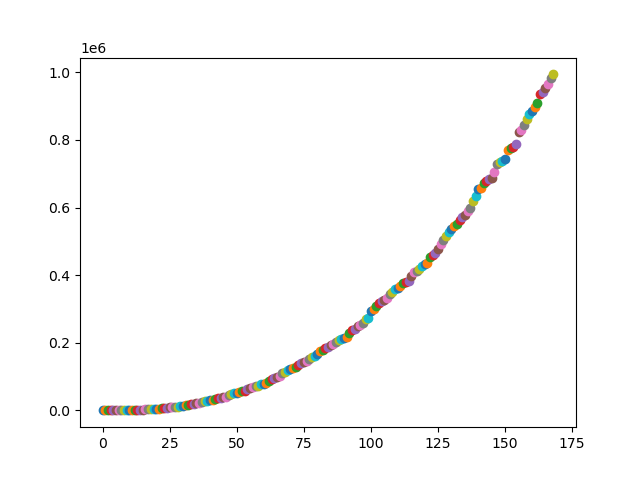
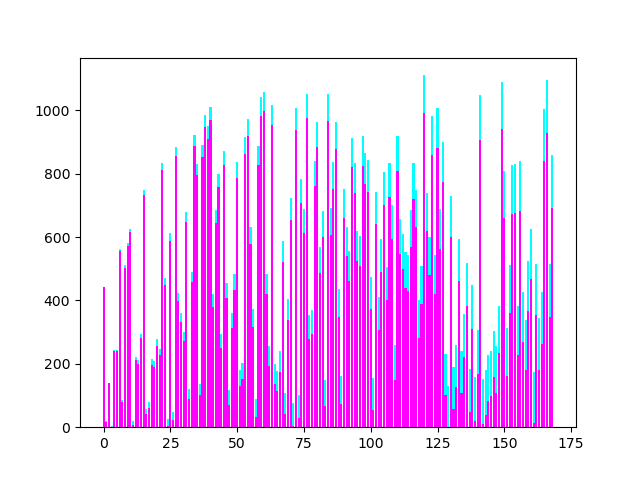
二つ目は素数と次の素数を足したもののグラフ、三つめは、それまでの素数の合計のグラフです。
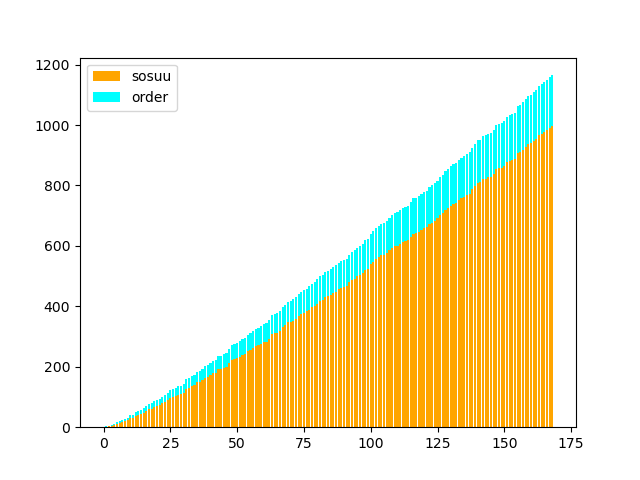
※4つ目のグラフは、同じように素数を使っていますが、全く別のコードからつくりました。他のグラフも、多少式や値を変えて作っています。
結論
素数は面白い