覚えたてのベイジアンネットワークで、住宅価格の関係性を探ってみた

背景

因果推論について勉強していて、ベイジアンネットワークのPythonによる構築について学んだので、さっそく実データに使ってみようと思いました。

実行環境

• Python3
• Google Colaboratory
• Windows10

ベイジアンネットワークとは？

　ベイジアンネットワークとは、それぞれの変数間の因果関係について調べる「因果推論」というジャンルの一つで、変数間の因果性や関係をグラフ構造で表そうとする手法です。「ベイズの定理」という統計学やデータサイエンスではおなじみの手法を使います。
　AICやBICなどの評価指標を使った方法や、カイ二乗検定など、条件付きの独立性の検定を用いた方法などがあります。今回は、後者の方法で実装していきます。
　ベイジアンネットワークについての詳しい解説は、この辺りを御確認ください。
https://www.msiism.jp/article/what-is-bayesian-network.html
https://www.headboost.jp/bayesian-network/
https://www.youtube.com/watch?v=zYKOL5RpVbo

注意点

• 私自身覚えたてということもあり、細かい説明はしていないところもあります。
• 基本的には、『つくりながら学ぶ！　Pythonによる因果分析　因果推論・因果探索の実践入門』という本を参考にコードを作成しました。
• 統計検定2級程度の内容が出てきますので、ある程度の統計の基礎知識が必要となります。

実装

まずは2種の神器(?)、ナムパイ様とパンダス様をありがた～く召喚させていただきます。

import numpy as np
import pandas as pd

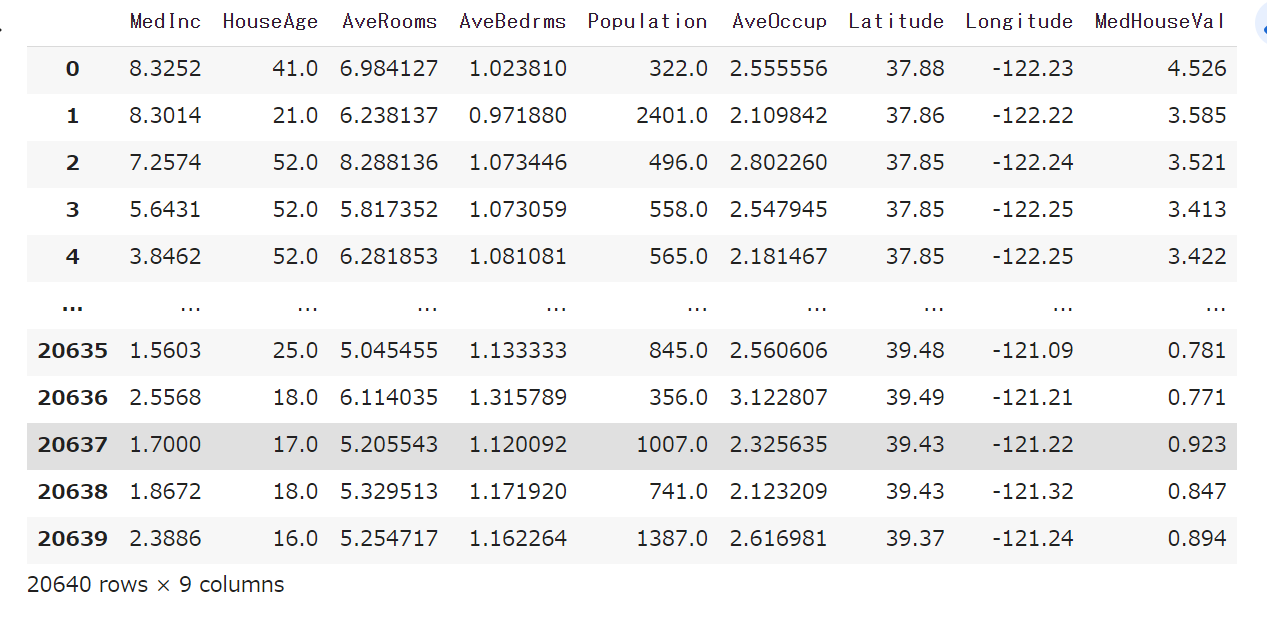
　次にカリフォルニアの住宅価格のデータセットをscikit-learnで読み込みます。正直、このデータセットについてはなんでもよかったです。なるべく実社会に即していて、単純そうなものを選びました。

各変数について
その他のsklearnのデータセットについて

from sklearn.datasets import fetch_california_housing
data = fetch_california_housing()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['MedHouseVal'] = data.target
df

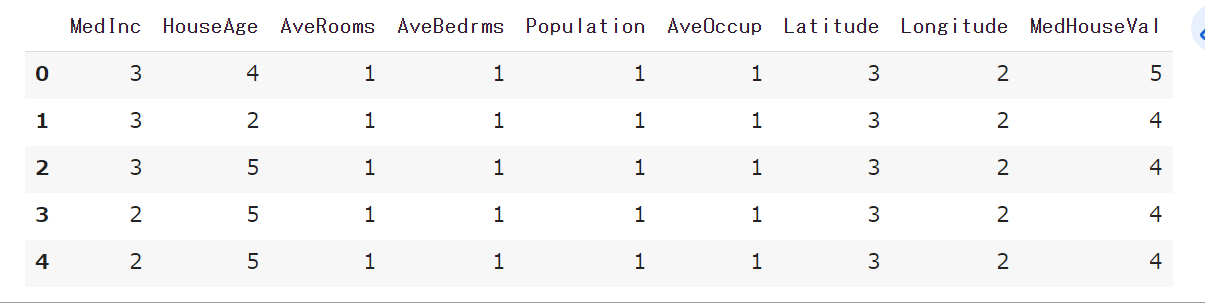
　次に、ベイジアンネットワークでは各データの値が離散値でなければならないので(条件付き確率を求めたいから)、cut関数を使います。retbins=Trueで、どの値が境界となって各クラスに分けられたかも保存しておくことができます。

# データを区切る
df_bin = df.copy()

df_bin["MedInc"], MedInc_bins = pd.cut(df["MedInc"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["HouseAge"], HouseAge_bins = pd.cut(df["HouseAge"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["AveRooms"], AveRooms_bins = pd.cut(df["AveRooms"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["AveBedrms"], AveBedrms_bins = pd.cut(df["AveBedrms"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["Population"], Population_bins = pd.cut(df["Population"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["AveOccup"], AveOccup_bins = pd.cut(df["AveOccup"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["Latitude"], Latitude_bins = pd.cut(df["Latitude"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["Longitude"], Longitude_bins = pd.cut(df["Longitude"], 5, labels=[1,2,3,4,5], retbins=True)
df_bin["MedHouseVal"], Longitude_bins = pd.cut(df["MedHouseVal"], 5, labels=[1,2,3,4,5], retbins=True)

df_bin.head()

　さて、ここからが本番です。まず、「0次の独立性の検定」というものを行います。どちらの変数にも条件を付けずに、2変数が互いに独立かどうかを調べます。独立性のカイ二乗検定を一からコードを書くこともできるでしょうが、ここではpgmpyというライブラリを使います。(注意：2023/4/11時点の最新バージョンだと、それまで使えていた関数が一部使えなくなっているので、バージョンは合わせて使った方が無難です。ネットに乗っている情報の大半が、この過去のバージョンでの書き方をしています。)

!pip install pgmpy==0.1.9

from pgmpy.estimators import ConstraintBasedEstimator

est = ConstraintBasedEstimator(df_bin)

# 0次の独立性の仮定

print('===========MedInc=============')
print(est.test_conditional_independence('MedInc', 'HouseAge', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'AveRooms', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'AveBedrms', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'Population', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'AveOccup', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('MedInc', 'MedHouseVal', method='chi_square', tol=0.05))
print('==========HouseAge==============')
print(est.test_conditional_independence('HouseAge', 'AveRooms', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'AveBedrms', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'Population', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'AveOccup', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('HouseAge', 'MedHouseVal', method='chi_square', tol=0.05))
print('============AveRooms============')
print(est.test_conditional_independence('AveRooms', 'AveBedrms', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveRooms', 'Population', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveRooms', 'AveOccup', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveRooms', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveRooms', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveRooms', 'MedHouseVal', method='chi_square', tol=0.05))
print('============AveBedrms============')
print(est.test_conditional_independence('AveBedrms', 'Population', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveBedrms', 'AveOccup', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveBedrms', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveBedrms', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveBedrms', 'MedHouseVal', method='chi_square', tol=0.05))
print('============Population============')
print(est.test_conditional_independence('Population', 'AveOccup', method='chi_square', tol=0.05))
print(est.test_conditional_independence('Population', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('Population', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('Population', 'MedHouseVal', method='chi_square', tol=0.05))
print('===========AveOccup=============')
print(est.test_conditional_independence('AveOccup', 'Latitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveOccup', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('AveOccup', 'MedHouseVal', method='chi_square', tol=0.05))
print('===========Latitude=============')
print(est.test_conditional_independence('Latitude', 'Longitude', method='chi_square', tol=0.05))
print(est.test_conditional_independence('Latitude', 'MedHouseVal', method='chi_square', tol=0.05))
print('============Longitude============')
print(est.test_conditional_independence('Longitude', 'MedHouseVal', method='chi_square', tol=0.05))

　とにかくごり押しで2組のペアすべてについて独立性を検定すると、以下のような出力となります。

===========MedInc=============
False
True
True
False
False
False
False
False
==========HouseAge==============
False
True
False
True
False
False
False
============AveRooms============
False
True
True
False
False
True
============AveBedrms============
True
True
False
False
True
============Population============
False
True
True
False
===========AveOccup=============
False
True
True
===========Latitude=============
False
False
============Longitude============
False

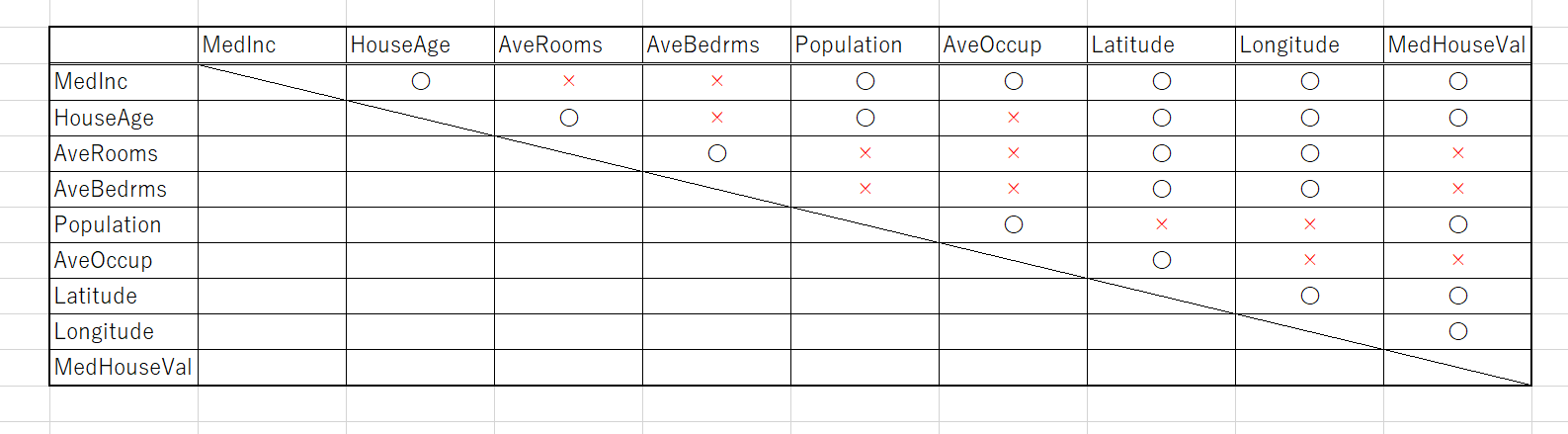
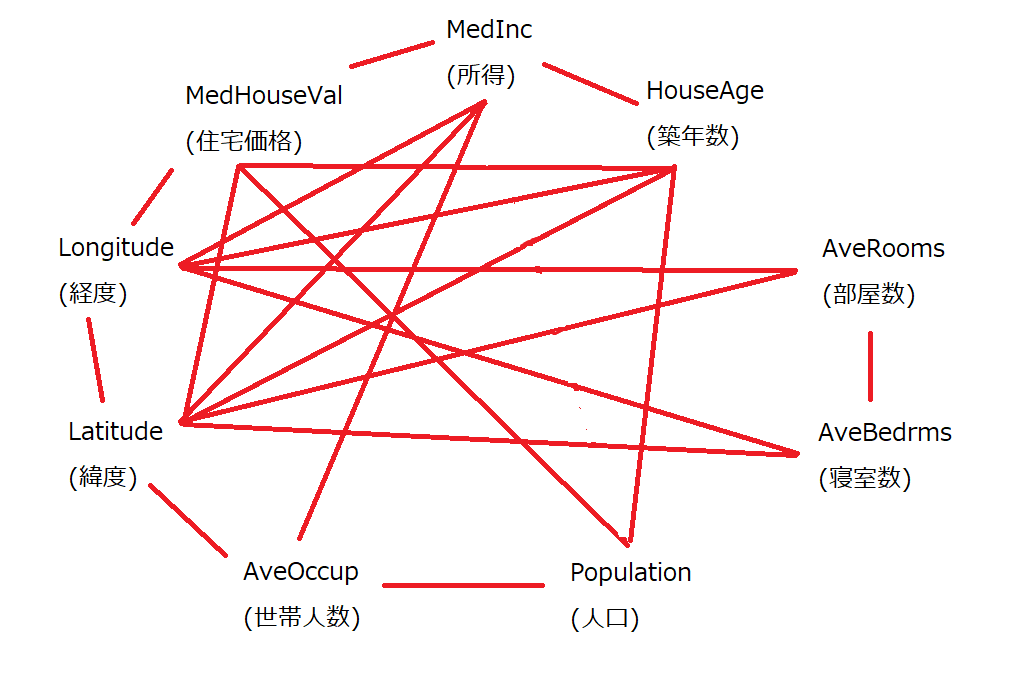
このうち、Trueとなったペアが、「互いに独立」と判断されたものです。これを書き出してみます。

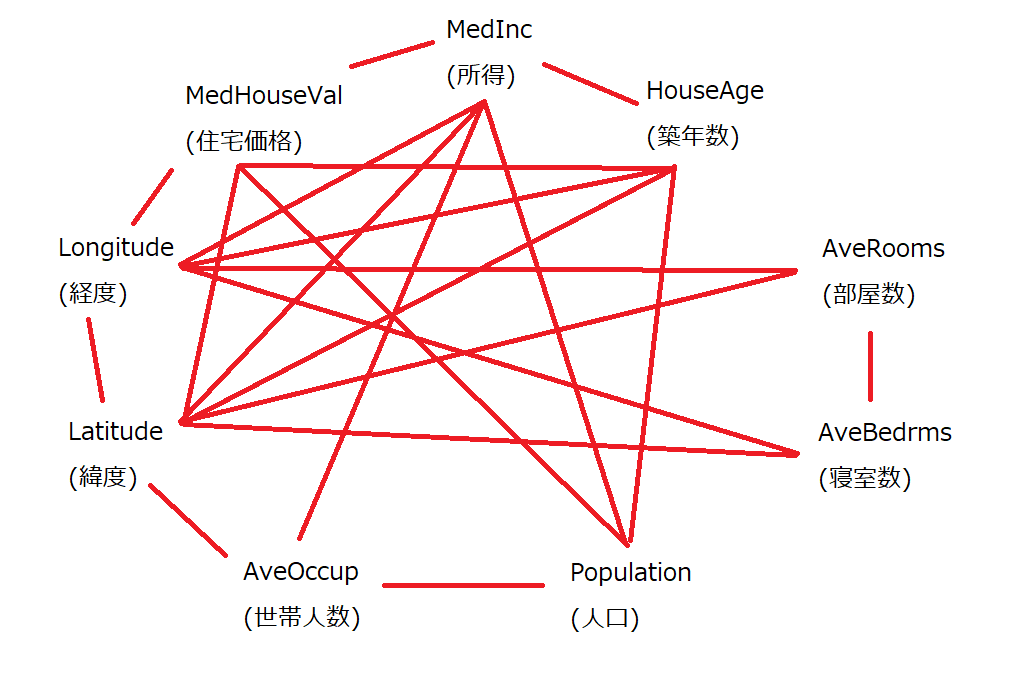
　赤字で×がついているものが「互いに独立」な組み合わせなので、これらをつなぐエッジ(辺)を削除します。

　このようになりました。変数が9個あって九角形になるので、なかなかいびつな図になりました(汗
　部屋数や寝室数は他の変数とあまり関係していなかったり、築年数と世帯人数が関連していなかったりします。そりゃそうですよね。部屋が多いのと築年数とか関係ないですし、築年数が古い建物は一人暮らしの人もファミリー層も住みますよね。意外なところだと、人口は緯度経度とあまり関係ないようです。

　さて、なんとなく現実の常識とも合ってそうなのを確認したところで、次は「1次の独立性」についてです。
　2つの変数の関係について、別のある1つの変数を条件として付けた条件付き確率を使って、独立性を調べます。例えば、MedIncであれば、他の6つの変数と関連がある(独立でない)ので、6×5=30通りの組み合わせを調べます。(例: CI(MedInc, HouseAge | Population) Populationを条件とした場合の、MedIncとHouseAgeの条件付き独立関数)。

# 1次の独立性の検定 変数MedInc

# Warningが出ると見づらいので、Warningを表示させない
import warnings
warnings.simplefilter('ignore')

print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['Population'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['AveOccup'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['Longitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Population', ['AveOccup'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Population', ['Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Population', ['Longitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Population', ['MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['Longitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['Longitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Longitude', ['MedHouseVal'], method="chi_square", tol=0.05
))

出力結果

False
False
False
False
False
False
False
True
True
False
False
False
False
False
False

　ここでさらに、Trueが出たものは独立と判断されました。今回は条件付き独立なので、例えば最初にTrueが出た8番目の CI(MedInc, Population | Longitude)なら、MedIncとLongitudeが関連している(先ほどのグラフで変数間が辺でつながっている)なら、MedIncとPopulationは関連していない(互いに独立)こととします。これをTrueが出たすべての組み合わせについて検討すると、今回はMedInc, Population間のエッジ(辺)だけ消すことができました。まぁ、所得が多い人が多い地域が人口が多いとは限りませんしね。今回も妥当な結果なのではないでしょうか。

(線消すの下手すぎ...(ペイントで作成))

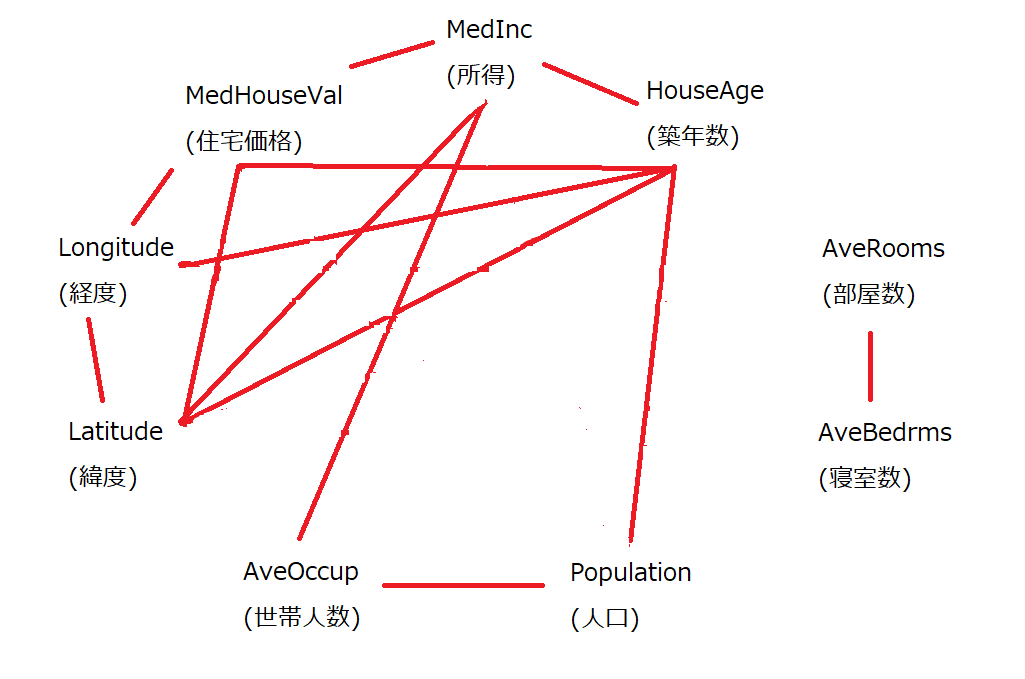
　で、それをすべての変数についてすべての組み合わせ(一度消した関連は考える必要はない)を頑張って検定して、それらをすべて消していくと、こうなります。

　相変わらず消すのが下手ですね。やはり部屋の数は他の変数とあまり関係なく、築年数や住宅価格が割と色々な変数と関係あるみたいです。まあそうでしょうね。意外に緯度も今回の場合は様々な変数に関連があるようですね。

　で、同じように次は「2次の独立性」も調べるのですが、今回はすべてFalseとなり、ここでいったん検定は終わりです。

print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['AveOccup', 'Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['AveOccup', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'HouseAge', ['Latitude', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['HouseAge', 'Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['HouseAge', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'AveOccup', ['Latitude', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['HouseAge', 'AveOccup'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['HouseAge', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['AveOccup', 'MedHouseVal'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'MedHouseVal', ['HouseAge', 'AveOccup'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'MedHouseVal', ['HouseAge', 'Latitude'], method="chi_square", tol=0.05
))
print(est.test_conditional_independence(
    'MedInc', 'MedHouseVal', ['AveOccup', 'Latitude'], method="chi_square", tol=0.05
))

で、最後にこの出来上がったグラフの方向性を考えます。変数同士が繋がっているときに、どちらが原因でどちらが結果かを考えなければなりませんね。これは、例えばMedHouseVal - MedInc - HouseAgeのようにV字でつながっているところを探して、その真ん中の部分を条件として先ほどと同じように条件付き独立を調べれば良いようです。独立でない場合は、両端の変数が原因、真ん中の変数が結果となるそうです。

# MedInc - HouseAge - MedHouseVal
print(est.test_conditional_independence(
    'MedInc', 'MedHouseVal', ['HouseAge'], method="chi_square", tol=0.05
))

# MedInc - HouseAge - Longitude
print(est.test_conditional_independence(
    'MedInc', 'Longitude', ['HouseAge'], method="chi_square", tol=0.05
))

# MedInc - HouseAge - Latitude
print(est.test_conditional_independence(
    'MedInc', 'Latitude', ['HouseAge'], method="chi_square", tol=0.05
))

# MedInc - HouseAge - Population
print(est.test_conditional_independence(
    'MedInc', 'Population', ['HouseAge'], method="chi_square", tol=0.05
))

# Population - AveOccup - MedInc
print(est.test_conditional_independence(
    'Population', 'MedInc', ['AveOccup'], method="chi_square", tol=0.05
))

# HouseAge - Latitude - MedInc
print(est.test_conditional_independence(
    'HouseAge', 'MedInc', ['Latitude'], method="chi_square", tol=0.05
))

# HouseAge - Latitude - Longitude
print(est.test_conditional_independence(
    'HouseAge', 'Latitude', ['Longitude'], method="chi_square", tol=0.05
))

# HouseAge - Latitude - MedHouseVal
print(est.test_conditional_independence(
    'HouseAge', 'MedHouseVal', ['Latitude'], method="chi_square", tol=0.05
))

# HouseAge - Longitude - MedHouseVal
print(est.test_conditional_independence(
    'HouseAge', 'MedHouseVal', ['Longitude'], method="chi_square", tol=0.05
))

# HouseAge - MedHouseVal - Latitude
print(est.test_conditional_independence(
    'HouseAge', 'Latitude', ['MedHouseVal'], method="chi_square", tol=0.05
))

# HouseAge - Population - AveOccup
print(est.test_conditional_independence(
    'HouseAge', 'AveOccup', ['Population'], method="chi_square", tol=0.05
))

# HouseAge - MedHouseVal - MedInc
print(est.test_conditional_independence(
    'HouseAge', 'MedInc', ['MedHouseVal'], method="chi_square", tol=0.05
))

# MedHouseVal - MedInc - HouseAge
print(est.test_conditional_independence(
    'MedHouseVal', 'HouseAge', ['MedInc'], method="chi_square", tol=0.05
))

出力

False
False
False
True
False
False
False
False
False
False
False
False
False

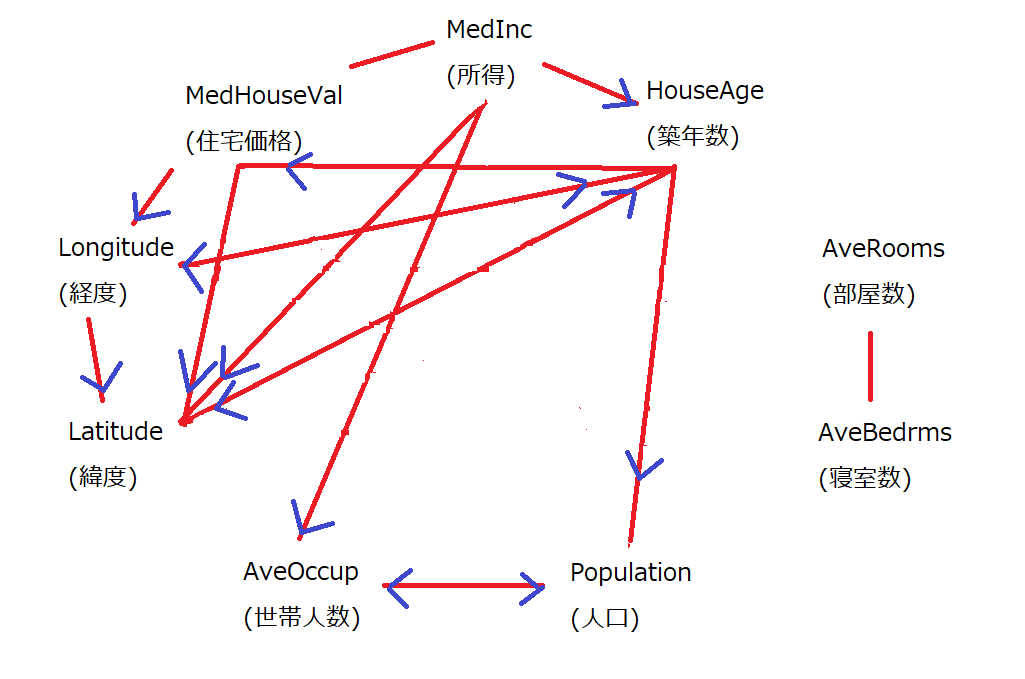
　今回の場合、ほとんど独立でないと出てしまったので、最終的な表は次のようになってしまいました。

　所得が世帯人数に影響を与えていたり、築年数がその地域の人口に関係するのはまあ分かるんですが、2つの変数間でどちらも原因と結果になってしまっていたり、普通因果逆じゃね？というものもあったりして、その辺りはやや不満です。でもまあ、ある程度は現実の感覚と相違ないモデルが作れたのではないでしょうか。

終わりに

　今回普段挙げなそうな統計分析の話で記事を書いてみました。至らない点も多いと思うので、訂正等あれば教えていただけると幸いです。
　でも今回やってみて、めちゃくちゃkaggleなどのコンペでも使えそうだなと思いました。シンプルな工程ながら、割と現実に即したしっかりとした説明になっていますし、特に家賃予測などは説明変数が多かったりして、どの変数とどの変数がどのように関連しているのかが分かりにくかったりもするので、序盤のEDA(データ分析)だけでなく、回帰分析をする際の多重共線性防止にも使えそうだなと思いました。
　先程ChatGPTについてニュースで触れられていました。最近何かとAIの話題が盛んですね。次はGPT3の実装方法とか勉強してみようかな～なんて。ちなみに好きな深層学習モデルはVisionTransformerとGANです。データサイエンス界隈では、そういうノリで、好きなモデルとか言いあったりはしないのかな～？

　じゃ～ね～また会う日まで

参考

・カリフォルニアの住宅価格データセットについて
https://atmarkit.itmedia.co.jp/ait/articles/2201/31/news042.html

・ベイジアンネットワークの実装について

『つくりながら学ぶ！　Pythonによる因果分析　因果推論・因果探索の実践入門』著：小川雄太郎