LoginSignup
8
16
@yasuyuki-s(Y S)

Pythonでポートフォリオ分析（過去データに基づく最適な資産構成比の探索）

Last updated at Posted at 2023-11-26

目的

  • Pythonを用いてポートフォリオを構成する各資産の過去データの統計解析（リスク、リターン、相関係数）を行う
  • 得られた統計解析結果を用いて、ポートフォリオにおける最適な資産構成比を探索し、効率的フロンティア（リスク・リターン分布）を出力する
  • 計算結果として得られるリスク・リターンは、以下の長期投資シミュレーションのインプットとしても利用可能

計算の概要

  • yfinanceを用いてYahoo! Financeより各資産の過去データを取得
  • Pandas, Numpyを用いて各資産の統計解析を実施（必要に応じて為替を考慮）
  • モンテカルロ法により様々な資産構成比を探索し、シャープレシオが最大となる組み合わせを出力
  • Plotlyを用いてリスク・リターンのインタラクティブな散布図を出力

実行例

  • 今回作成した解析用のクラスであるasset_analysisの実行例を示します。
  • 実装方法は後述します。

1. 各資産の過去データの取得、統計解析

#各資産のYahoo Financeにおけるティッカーを入力
assets = ["IVV","ACWI","EEM","EWJ","AGG","IGOV","VNQ","GLD"]
test = asset_analysis(assets)
#USD換算での分析実行
test.history_r("2003-12-01","2023-11-01","USD")
#JPY換算での分析実行
test.history_r("2003-12-01","2023-11-01","JPY")
  • リストassetsで入力した各資産について、Yahoo Financeより過去データを取得し、指定の期間・通貨立ての統計解析を実施します
  • 例として、以下の株式・債券・金等の8つETFの過去20年間のデータを参照しています
カテゴリ 資産名 ティッカー
米国株式 iシェアーズ・コア S&P 500 ETF IVV
全世界株式 iシェアーズ MSCI ACWI ETF ACWI
新興国株式 iシェアーズ MSCI エマージング・マーケット ETF EEM
日本株式 iシェアーズ MSCI ジャパン ETF EWJ
米国債券 iシェアーズ・コア 米国総合債券市場 ETF AGG
先進国債券 iシェアーズ 世界国債（除く米国）ETF IGOV
米国REIT バンガード不動産ETF VNQ
金 SPDRゴールド・シェア ETF GLD

実行結果

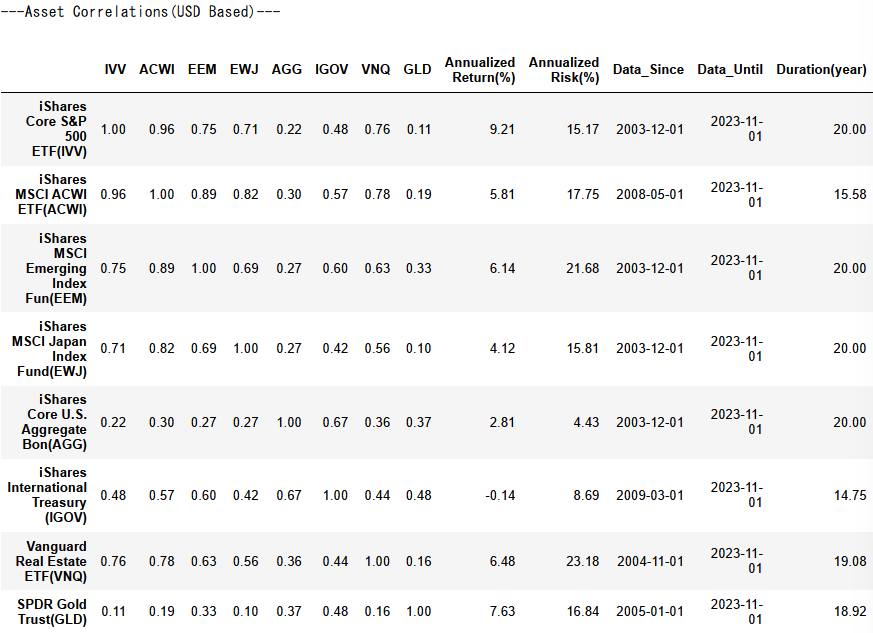
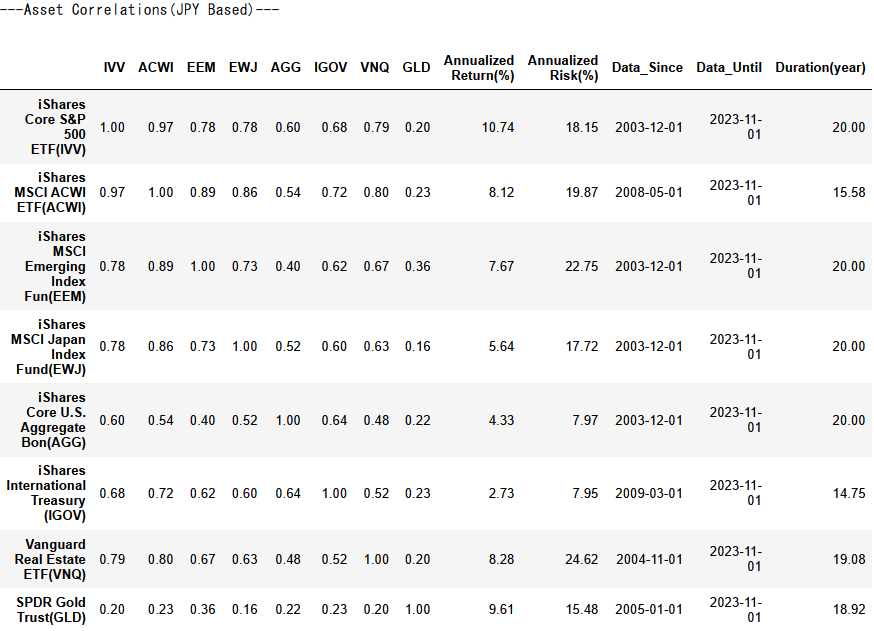
image.png
image.png

  • 各資産の相関係数、年換算の対数収益率・標準偏差、有効データ期間を出力しています
  • 円建てでは、ドル建てに比べて総じてリターン・リスクともに大きくなる傾向にあり、また株式と債券の相関もより強くなり、為替の影響を強く受けていることが見て取れます。
  • 一方、金(GLD)については、円建てでもその他の資産との相関係数が低いことが特徴的です。
  • なお、有効データ期間であるDurationが20未満になっているものについては、取得できたデータが不足しており、取得できた限りのデータを用いた計算結果となっています

2. ポートフォリオの最適資産構成の探索

#ポートフォリオのモンテカルロシミュレーションを実行(パラメータは直前の分析(history_r)の結果に基づく)
test.port_mc()
  • モンテカルロ法を用いて様々な資産構成の組み合わせにおけるリターン・リスクを計算します。
  • 各資産の統計パラメータは、直前の解析を引継ぎ円建ての値が使用されます。

実行結果

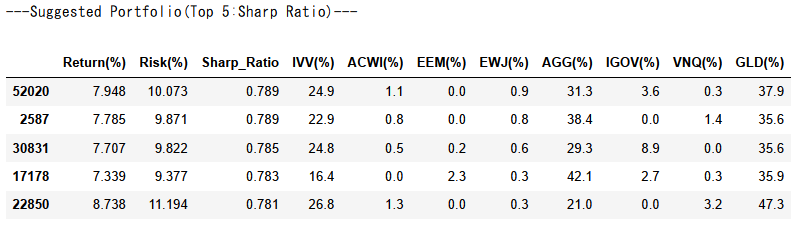
image.png

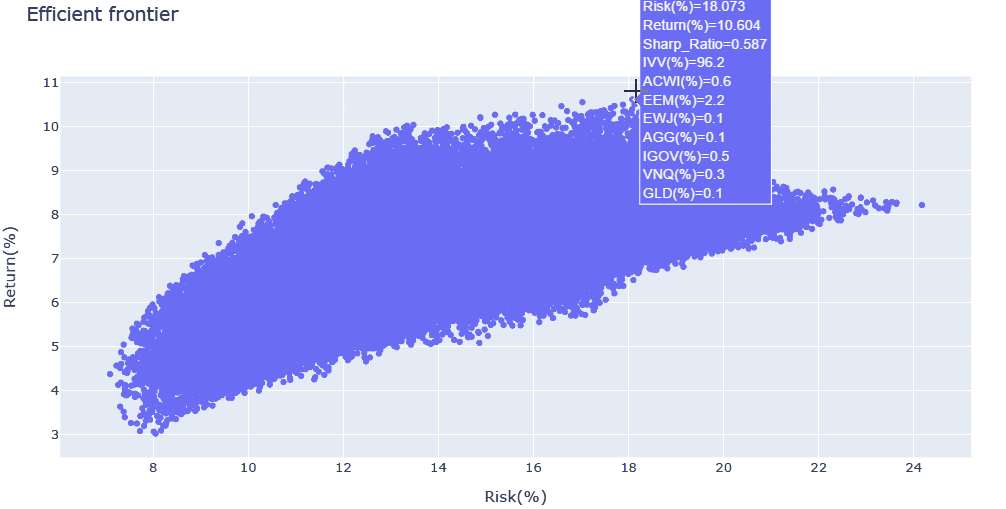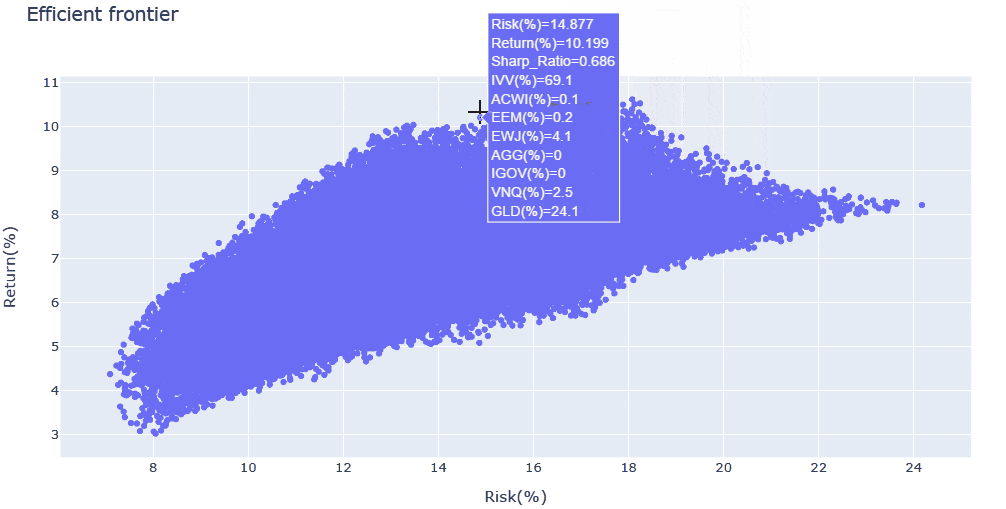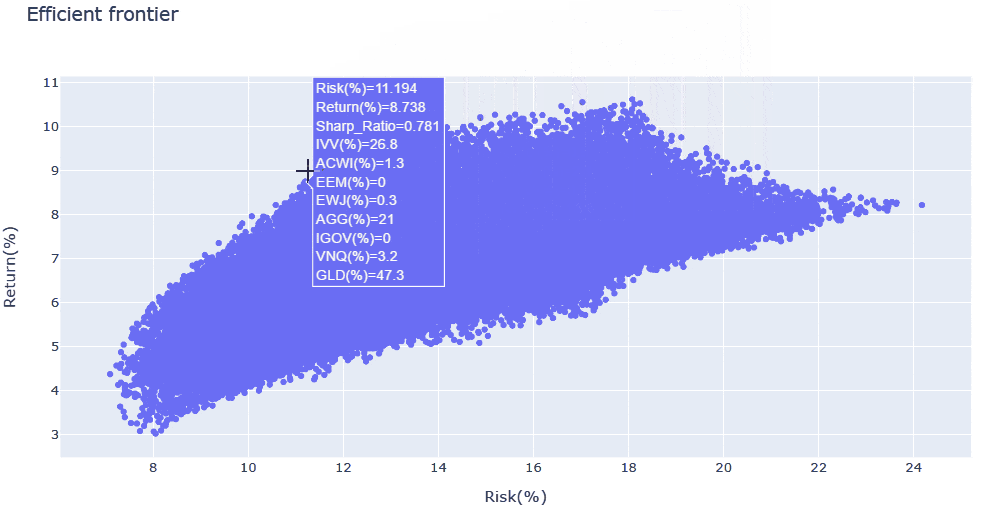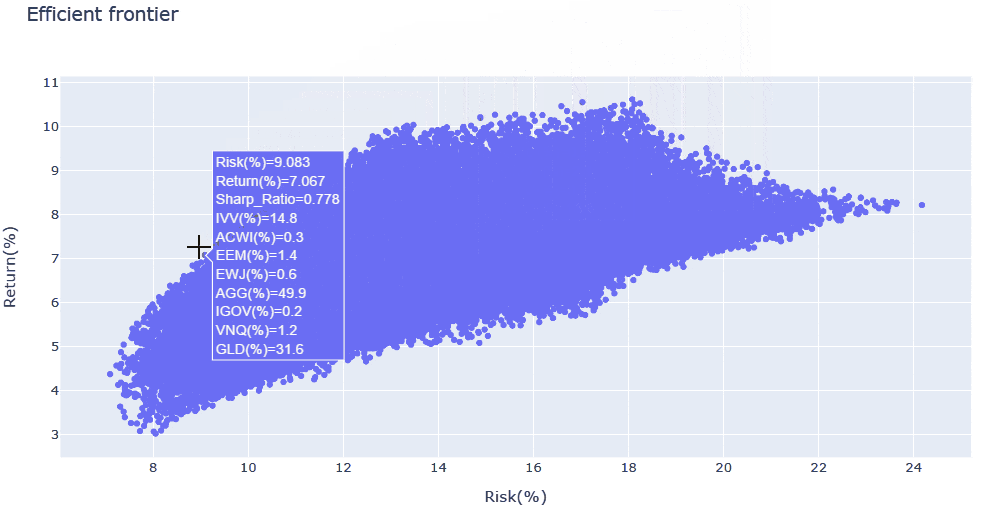
Animation.gif

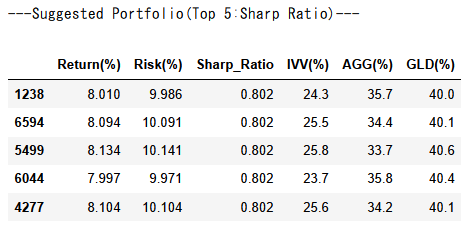
  • シャープレシオの上位5つのケースと、全計算結果のリスク・リターン分布を出力しています。
  • リスク・リターン分布はPlotlyで出力しており、拡大・縮小やマウスオーバーでの情報表示が可能です
  • 今回の例では、変数が多いため効率的フロンティアが不明瞭ですが、シャープレシオの最大化にあたり、IVV・AGG・GLDの3資産の影響が支配的であることがわかりました
  • そこで、対象資産を上記の3つに絞った上で、再度解析を回してみます
assets = ["IVV","AGG","GLD"]
test = asset_analysis(assets)
test.history_r("2003-12-01","2023-11-01","JPY")
test.port_mc()

image.png
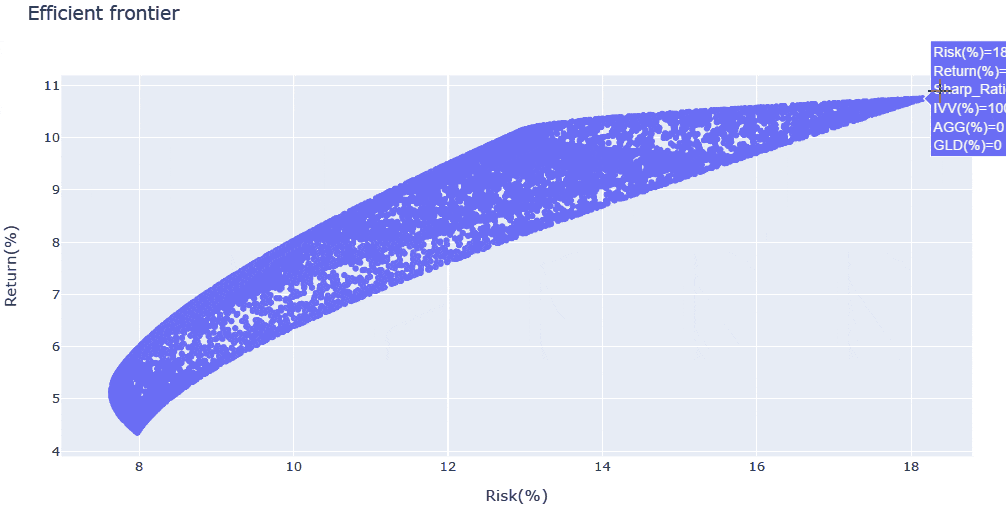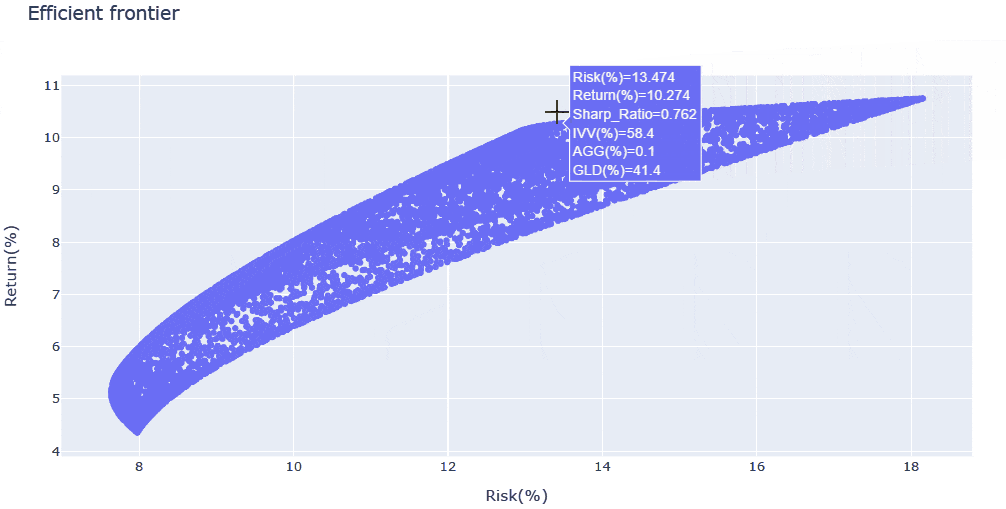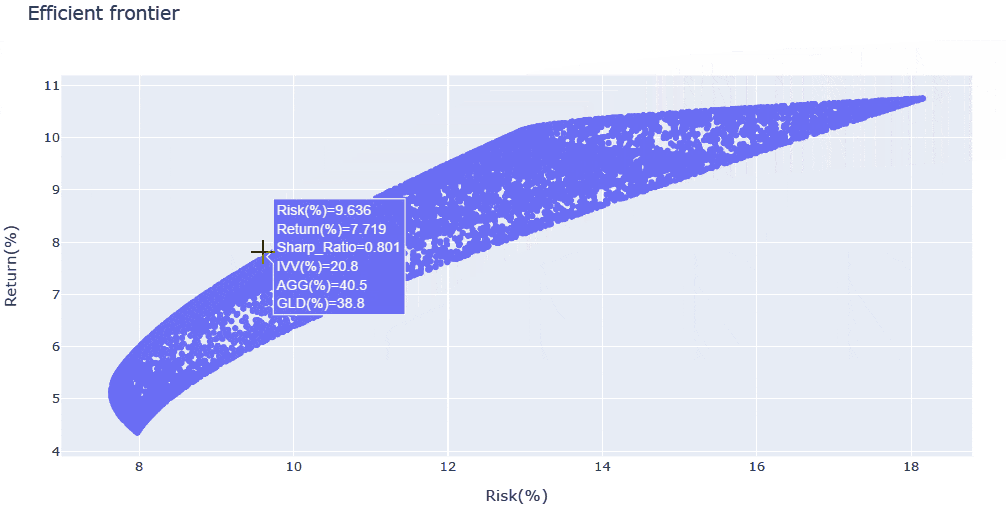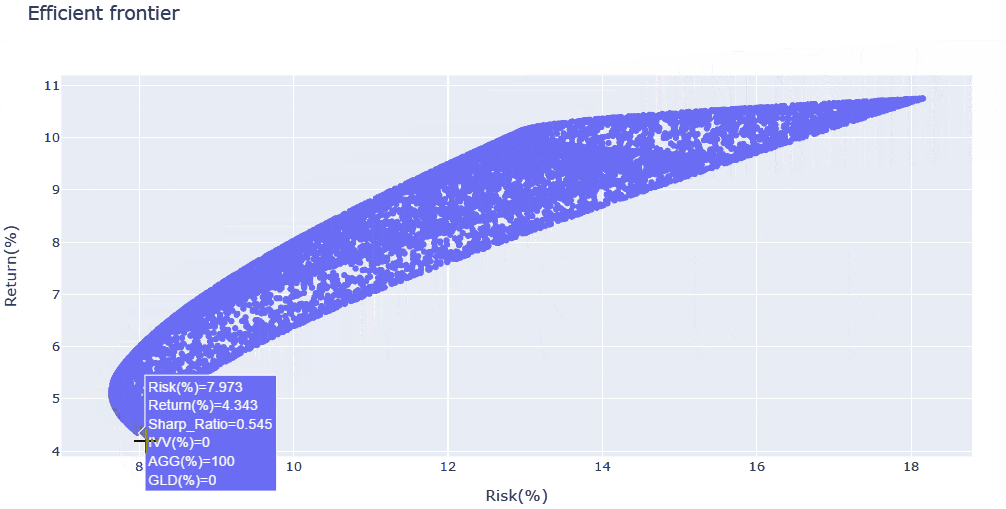
Animation2.gif

  • 構成資産数を絞ったため、今度は効率的フロンティアが明瞭になった計算結果が得られました。
  • シャープレシオを重視するのであれば、解析結果で得られたIVV・AGG・GLDの構成比を採用することも一案ですし、さらに大きなリターンを志向して、リターン10%付近の効率的フロンティア曲線の変曲点周辺（IVV:GLD=50%:50%程度）を狙うのも面白いかもしれません。

実行例：おまけ（インデックスETFと、インデックスとの比較）

  • ETFや個別銘柄に加えて、主要なインデックスの過去データも取得可能です
  • S&P500を参照する主要なETF2種と、S&P500の過去10年分のデータを比較してみました
assets = ["IVV","VOO","^SPX"]
sp500 = asset_analysis(assets)
sp500.history_r("2013-12-01","2023-12-01","JPY")

image.png

  • IVVもVOOも、S&P500との相関係数は1.0と、忠実にインデックスに連動しています。
  • 両ETF間の差はほとんどなく、いずれもS&P500よりも年率で2%近くリターンが大きくなっています。これは両ETFには配当が含まれていることが原因と考えられます。

実装方法

  • ソースコード全文は下記を参照してください

  • asset_analysisクラスの構成は下記の通りです
 #ライブラリ読み込み
import yfinance as yf   
from datetime import datetime
import numpy as np
import plotly.express as px
import pandas as pd
from IPython.display import display

class asset_analysis:
    #初期化時の処理、過去データの取得
    def __init__(self, asset_list):

    #各資産の過去データの統計解析
    def history_r(self,start,end,currency):

    #ポートフォリオのモンテカルロシミュレーション
    def port_mc(self):

計算の流れ

  1. 各資産の過去データの取得
  2. 通貨単位の変換用の為替過去データの取得（必要に応じて）
  3. 対数収益率の計算
  4. 解析対象期間のデータを抽出
  5. 各資産の年率換算リターン・リスクを出力
  6. モンテカルロ法により様々な資産構成比でのリスク・リターンを計算
  7. 計算結果を出力

1. 各資産の過去データの取得

class asset_analysis
def __init__(self, asset_list):
    #各資産のティッカーを格納
    self.tickers = asset_list
    self.assets_df = []
    self.currencies = []
    self.shortnames = {}
    for asset in asset_list:
        #Yahoo Financeより各資産の過去データを取得
        df = yf.download(asset,period="max",interval='1mo',progress=False)
        self.assets_df.append(df)
        #currenciesに各資産の通貨単位を格納
        self.currencies.append(yf.Ticker(asset).info["currency"])
        #shortnamesに各資産の名前を格納
        self.shortnames[asset]=yf.Ticker(asset).info["shortName"]+"("+asset+")"
        print("Asset data download completed("+ asset +")")
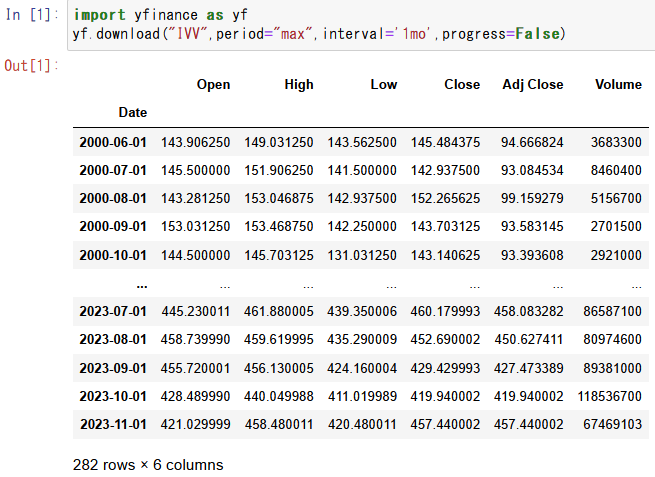
  • df = yf.download(asset,period="max",interval='1mo',progress=False)
    yfinanceを用いて指定された資産の月次データをYahoo Financeより取得します。
    実行例：
    image.png
  • self.currencies.append(yf.Ticker(asset).info["currency"])
  • self.shortnames[asset]=yf.Ticker(asset).info["shortName"]+"("+asset+")"
    指定された資産の通貨単位、名前などを取得します。
    実行例：
    image.png

2. 通貨単位の変換用の為替過去データの取得（必要に応じて）

class asset_analysis
def history_r(self,start,end,currency):
    ##為替変換の前処理
    #各資産の通貨単位のユニークなリストを作成
    curr_set = set(self.currencies)
    ex_list = {}
    for asset_curr in curr_set:
        #各資産の通貨単位がアウトプットの通貨単位と異なる場合
        if asset_curr != currency:
            #通貨ペアを設定（例：USD/JPYの場合はUSDJPY）
            ex = asset_curr + currency
            #Yahoo Financeより指定通貨ペアの為替過去データを取得
            df = yf.download(ex+"=X",period="max",interval='1mo',progress=False)
            ex_list[ex]=df
            print("Exchange data download completed("+ex+")")
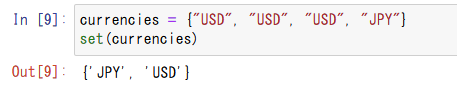
  • curr_set = set(self.currencies)
    setを用いて資産の通貨リスト一覧から重複を除いたユニークなリストを作成します
    実行例：
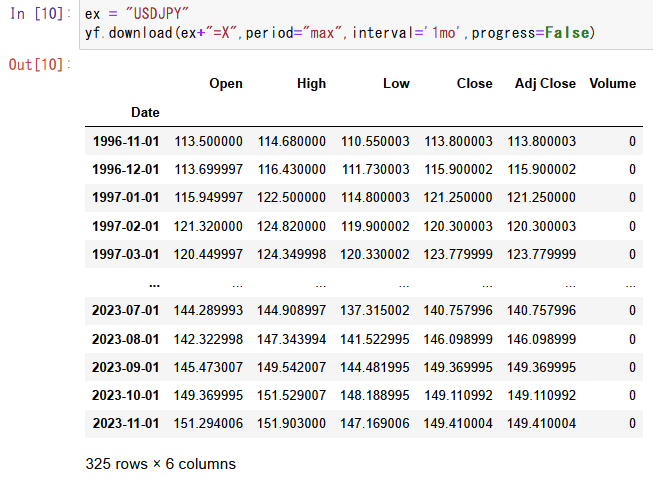
    image.png
  • yf.download(ex+"=X",period="max",interval='1mo',progress=False)
    yfinanceを用いて指定された通貨ペアの月次為替データをYahoo Financeより取得します。
    実行例：
    image.png

3. 対数収益率の計算

def history_r（続き）
##統計解析用データフレームの準備
df = pd.DataFrame()
for i in range(len(self.tickers)):
    df_tmp = self.assets_df[i].copy()
    df_tmp["lr"]=np.nan
    if self.currencies[i] != currency:
        #通貨単位が異なる場合は、為替データを掛けて通貨単位を揃えておく
        df_tmp["Adj Close"] = df_tmp["Adj Close"]*ex_list[self.currencies[i]+currency]["Adj Close"]
    for j in range(0,df_tmp.shape[0]-1):
        #各行の修正後終値（Adj Close）の値を用いて対数収益率lrを計算
        df_tmp.iloc[j+1,6] = np.log(df_tmp.iloc[j+1,4] /df_tmp.iloc[j,4])
    #各資産の対数収益率を格納           
    df[self.tickers[i]]=df_tmp["lr"]
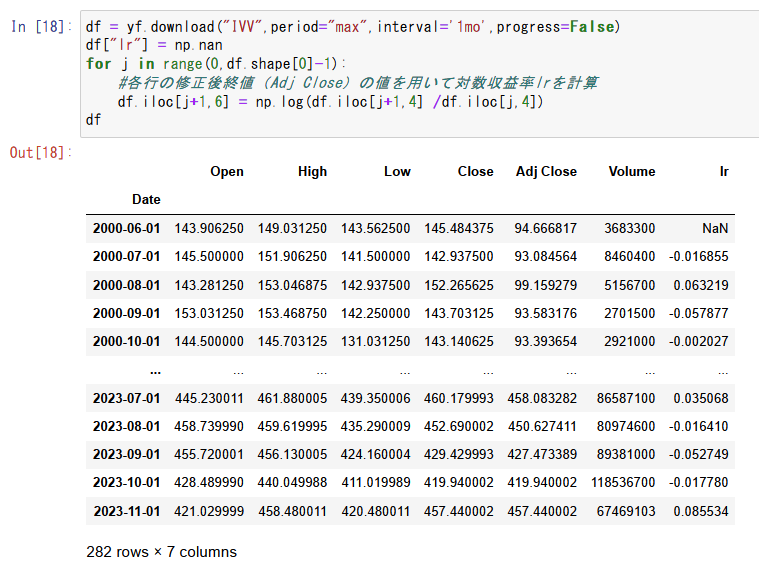
  • df_tmp.iloc[j+1,6] = np.log(df_tmp.iloc[j+1,4] /df_tmp.iloc[j,4])
    各資産の過去データのDataFrameのlr列に、対数収益率の計算結果を格納します
    実行例：
    image.png

4. 解析対象期間のデータを抽出

def history_r（続き）
#解析対象期間のデータを抽出しソート
df = df.sort_index().loc[start:end]
self.df_all = df.copy()
  • 引数として入力されたstart、endの期間内のデータのみを抽出します
  • 後段の処理（モンテカルロシミュレーション）に使うので、全資産の対数収益率のデータをself.df_allにコピーしておきます

5. 各資産の年率換算リターン・リスクを出力

def history_r（続き）
#各資産の対数収益率の相関係数を計算
df_list = round(df.corr(),2)

#出力のためのデータ加工
assets = df_list.index
for asset in assets:
    #年率換算したリターン、リスク（標準偏差）を出力
    df_list.loc[asset,["Annualized Return(%)","Annualized Risk(%)"]] = annualized(df[asset])
    df_tmp = df[asset].dropna()
    #有効データの始期、終期、有効データ期間を出力
    df_list.loc[asset,"Data_Since"] = df_tmp.index[0]
    df_list.loc[asset,"Data_Until"] = df_tmp.index[-1]
    df_list.loc[asset,"Duration(year)"] = round(df_tmp.shape[0] / 12,2)
#行名をティッカーから事前に取得した各資産の名前（shortname)に置換
df_list = df_list.rename(index=self.shortnames)
print("---Asset Correlations("+ currency +" Based)---")
display(df_list)

#リターン・リスクの年率換算
def annualized(df):
    #月次の対数収益率の平均、標準偏差を12ヵ月分（一年分）へ拡張
    mu = df.mean() * 12
    s = df.std() * np.sqrt(12)

    #パーセント表記へ変換
    mu2 = round((mu)*100,2)
    s2 = round(s*100,2)
    return mu2,s2
  • corr()を用いて各資産の対数収益率の相関係数を算出した後に、資産別の年率換算のリターン・リスク、有効データの期間等を新たな列としてDataFrameに追加し、出力しています。

6. モンテカルロ法により様々な資産構成比でのリスク・リターンを計算

class asset_analysis
#ポートフォリオのモンテカルロシミュレーション
def port_mc(self):
    #年率換算後の各資産の共分散を計算
    df_cov = self.df_all.cov() * 12
    #年率換算後の各資産の平均リターンを計算
    df_mean = self.df_all.mean() * 12
    
    #ポートフォリオの資産構成比
    port_weights = []
    #ポートフォリオのリターン
    port_return = []
    #ポートフォリオのリスク（標準偏差）
    port_risk = []
    #ポートフォリオのシャープレシオ
    sharpe_ratio = []
    
    #モンテカルロシミュレーション
    for r in range(1000*df_cov.shape[0]**2): #試行回数は変数の2乗で増減
        weight = np.random.chisquare(1,df_cov.shape[0]) #よりメリハリのきいた組み合わせを生成するため、カイ二乗分布で乱数生成
        #weight = np.random.random(df_cov.shape[0]) #一様分布で乱数生成
        weight = weight/np.sum(weight)
        port_weights.append(weight)
        #ポートフォリオのリターンを計算
        port_return.append(np.dot(df_mean, weight))
        #ポートフォリオのリスク(標準偏差）を計算
        port_risk.append((np.dot(weight.T, np.dot(df_cov, weight))) ** 0.5)
        #ポートフォリオのシャープレシオを計算
        sharpe_ratio.append(port_return[r]/port_risk[r])
  • モンテカルロ法による最適資産構成比の探索は、下記の記事を参考にさせていただきました。

  • weight = np.random.chisquare(1,df_cov.shape[0])
    資産構成比weightの作成には、一様分布ではなくカイ二乗分布に従う乱数を用いています。
    一様分布を用いて乱数生成した場合、概ねバランスよく各資産を保有するような構成比となる組合せが多く出力され、資産数が多くなった場合にリスク・リターン分布が平均付近に収斂され、効率的フロンティアが不明瞭になる傾向が見られます。
    こうした現象を回避するため、特定の資産に偏るような尖った構成比がより多く出力されるよう、カイ二乗分布に従う乱数を用いることとしました。
    乱数生成に一様分布を用いた出力例（上記例の8資産の場合）：
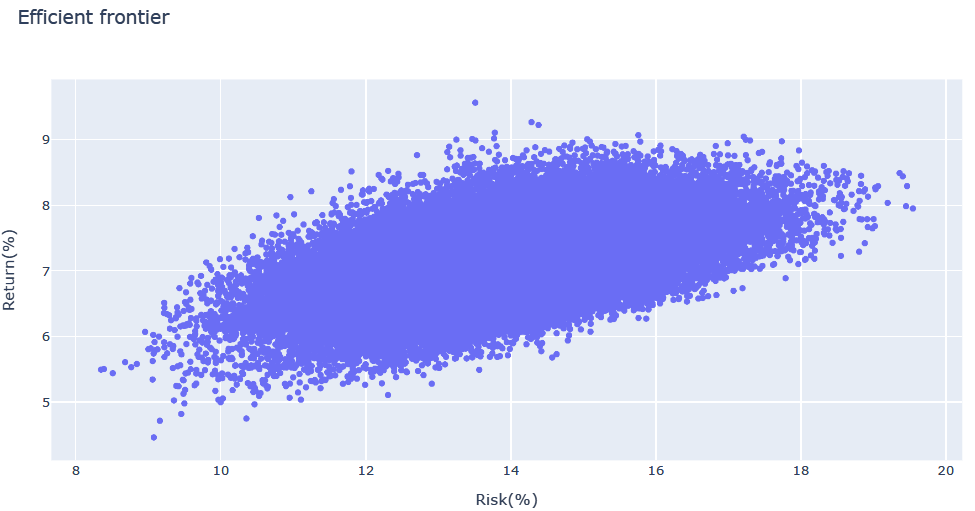
    image.png
    乱数生成にカイ二乗分布を用いた出力例（上記例の8資産の場合）：
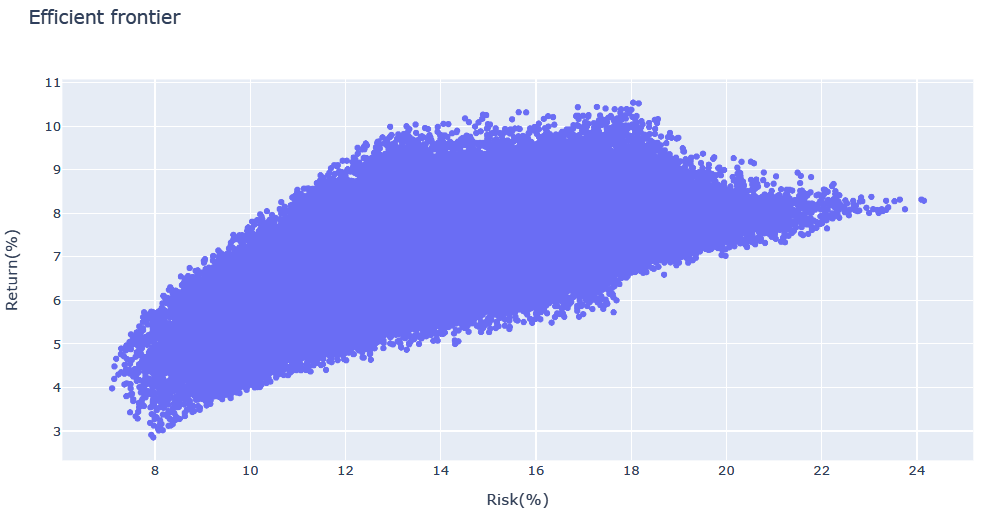
    image.png

7. 計算結果を出力

def port_mc（続き）
#df_resultに計算結果を格納
df_result = pd.DataFrame({'Return(%)': port_return,'Risk(%)': port_risk,'Sharp_Ratio': sharpe_ratio})
for w,ticker in zip(np.array(port_weights).T,self.tickers):
    df_result[ticker+"(%)"] = w
    df_result[ticker+"(%)"] = round(df_result[ticker+"(%)"]*100,1)
df_result= df_result.sort_values(by=['Sharp_Ratio'], ascending=False)
df_result["Return(%)"] = round(df_result["Return(%)"] * 100,3)
df_result["Risk(%)"] = round(df_result["Risk(%)"]*100,3)
df_result["Sharp_Ratio"] = round(df_result["Sharp_Ratio"],3)
print("---Suggested Portfolio(Top 5:Sharp Ratio)---")
display(df_result[0:5])
#Plotlyでリスク・リターンの散布図を描画
fig = px.scatter(
    data_frame=df_result,
    x='Risk(%)',
    y='Return(%)',
    hover_data = df_result.columns.values,
    title='Efficient frontier')
fig.update_layout(hovermode="closest")
fig.show()
  • df_resultへ計算結果を格納した後に、シャープレシオ上位5つの結果を表として出力しています。
  • シャープレシオの計算において、無リスク資産のリターンは考慮していません。
  • リスク・リターン分布はPlotlyで描画し、インタラクティブに計算結果を確認することが可能です。

参考文献

  • 背景となる現代ポートフォリオ理論の考え方は以下を参考にしています。

8
16
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
16