LoginSignup
104
128
@yasuyuki-s(Y S)

Pythonで長期積立投資シミュレーション

Last updated at Posted at 2023-11-28

目的

  • Pythonを用いて特定のリターン・リスク（標準偏差）を持つ資産に毎月積立投資を行った場合の長期資産推移を、モンテカルロ法によるシミュレーションで算定する

計算の概要

  • Pandas、Numpyを用いて、対象期間における月次の対数収益率を、正規分布に従う乱数として生成する
  • 得られた乱数を用いて、毎月積立投資を行った場合の資産推移をパーセンタイル値として出力する

(2024/1/29追記）

  • 実行例をWebアプリ化し、手軽に試せるようにしたものを投稿しました。

実行例

  • 今回作成した解析用のクラスであるasset_modelの実行例を示します。
  • 実装方法は後述します。

1. 資産のリターン・リスクを設定する

# 期待対数収益率、標準偏差（%,年換算）
mu = 8
s = 20

#リターンmu、リスクsのモデルを定義
model = asset_model(mu,s)
  • 対象資産の年次の対数収益率の期待値（平均）、標準偏差を入力します
  • 今回の例では、全世界株式(ACWI)を想定した値（期待リターン8%、リスク20%)を設定しています。
  • 任意のポートフォリオのリターン・リスクの算定には下記記事もご参考に。

2. モンテカルロシミュレーションを実行する

# 投資期間（年）
dur_y = 10
# 試行回数
n = 20000

#投資期間dur_y、試行回数nのモンテカルロシミュレーションを実行
model.run_mc(dur_y,n)
  • 投資期間、モンテカルロ法の試行回数を入力しモンテカルロシミュレーションを実施します。
  • 詳細は後述しますが、内部処理としては投資期間(月換算)×試行回数個の月次対数収益率を、前段で入力した期待値、標準偏差の正規分布に従い生成しています。
  • 投資期間が長くなると、計算にはちょっと時間がかかります。

3. 積立投資を行った場合の資産推移を算定

# 初期投資額
x_init = 0
# 毎月積立額
delta_m = 10

#初期投資x_init、毎月delta_mの積立投資を行った場合の資産推移を計算
model.exercise(x_init,delta_m)
  • 初期投資額、毎月積立額を入力し、前段で生成した対数収益率のデータを用いて、長期資産推移を算定します。
  • 今回の例では、初期投資額を0、毎月の積立額を10としています。

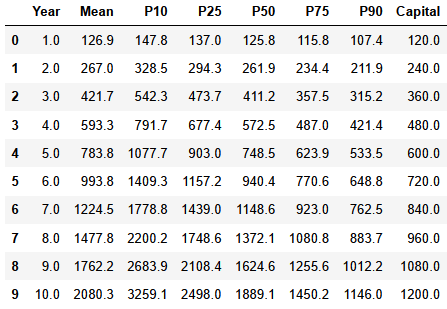
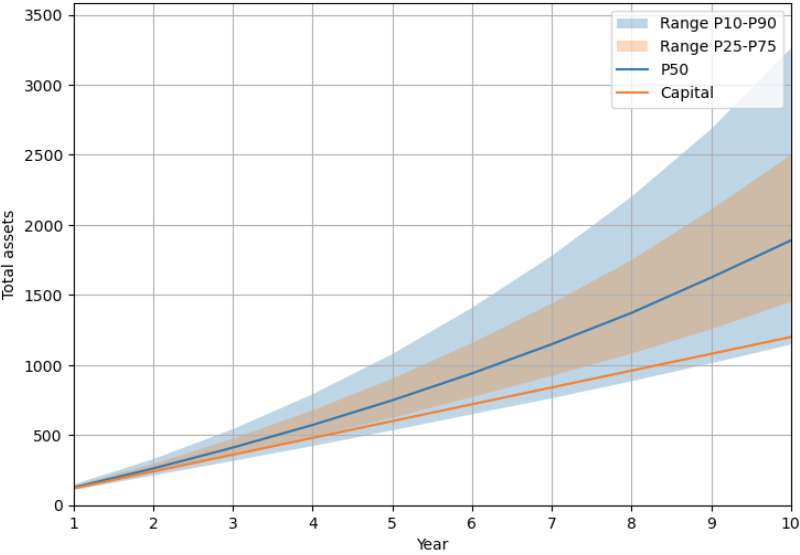
出力結果

image.png
image.png

  • モンテカルロシミュレーションに基づき、年毎の総資産額の分布の平均値、P10～P90のパーセンタイル値、累計投資額（元本）をそれぞれ出力しています
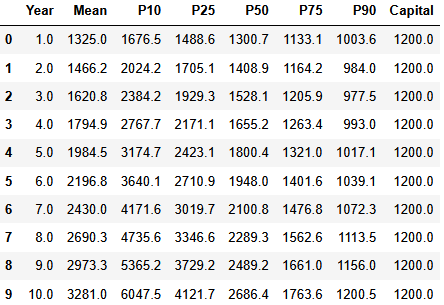
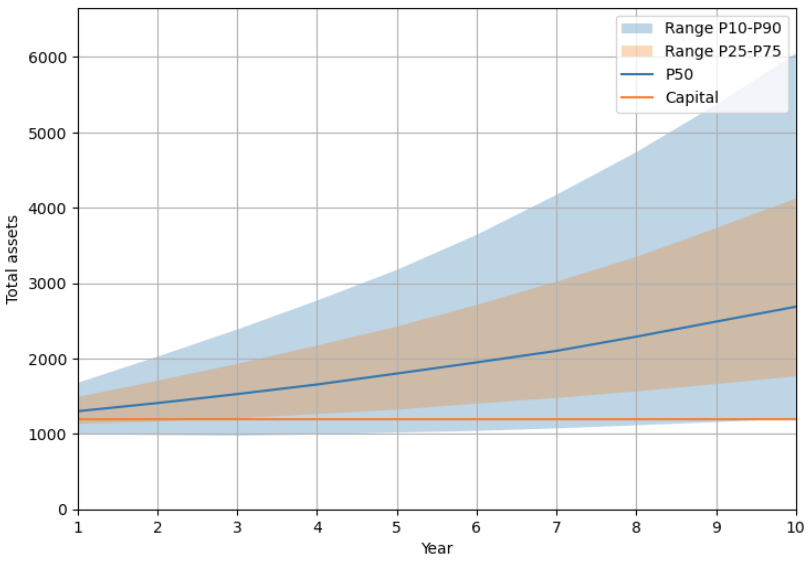
  • モデルと対象期間が同じであれば、exerciseのみを再度実行することで、異なる初期投資額、積立額での計算が可能です。
  • 例えば、上記の例における10年間の総投資額と同じ金額を、全て一括で初期投資し、積立は0とする場合は下記の通りになります。
# 初期投資額
x_init = 1200
# 毎月積立額
delta_m = 0

#初期投資x_init、毎月delta_mの積立投資を行った場合の資産推移を計算
model.exercise(x_init,delta_m)

image.png
image.png

  • 今回の例では、全額を一括投資するケースは積立投資のケースに比べ、運用期間の前半においてより大きな下振れリスクがある一方、10年後時点では下振れリスクに大きな違いはなく、より大きなアップサイドを期待できる結果となりました。

実装方法

  • ソースコード全文は下記を参照してください

  • asset_modelクラスの構成は以下の通りです
#ライブラリ読み込み
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from IPython.display import display

#対数収益率の正規分布を仮定した長期投資シミュレーションモデル
class asset_model:
    #初期化時の処理
    def __init__(self, mu_y, s_y):

    #対数収益率の長期モンテカルロシミュレーションを実施
    def run_mc(self, dur_y, n):
        
    #初期投資額x_init, 毎月積立額delta_mを投資した場合の資産推移を計算
    def exercise(self, x_init, delta_m):

計算の流れ

  1. 年次リターン・リスクを月換算
  2. 投資期間、試行回数に応じた数の対数収益率に相当する乱数を生成
  3. 投入資金の、各時点における推移を計算
  4. 計算結果を出力
  • 積立投資の長期資産推移の計算の考え方は以下の通りです。
  • ある時点$i$における資産価格を$P_i$としたとき、対数収益率$lr$は以下の通り表されます。
lr_{i+1}=\ln \frac{P_{i+1}}{P_{i}}
  • 上記の対数収益率の定義および対数の性質より、($t>i$)となる時点$i$で投資した金額$X_i$の、時点$t$における金額$X_{i,t}$は以下の通り求められます。
\begin{align}
X_{i,t} &=  X_i * (\frac{X_{i+1}}{X_{i}}*\frac{X_{i+2}}{X_{i+1}}* \dots *\frac{X_{t}}{X_{t-1}})  \\\
&=X_i * \exp (lr_{i+1}+lr_{i+2}+\dots+lr_t)
\end{align}
  • 以上より、時点$t$における積立投資の累計投資額$Capital_t$および総資産額$TotalAsset_t$は以下の通り求められます。
Capital_t = \sum_{i=0}^{t-1}X_i 

TotalAsset_t = \sum_{i=0}^{t-1}X_{i,t}
  • 各時点の投資額$X_i$は入力値として与えられます。
  • モンテカルロシミュレーションでは、対数収益率$lr$を乱数により生成します。

1. 年次リターン・リスクを月換算

class asset_model
def __init__(self, mu_y, s_y):
    #パーセント表記から少数へ変換
    mu_y = mu_y / 100
    s_y = s_y / 100
    #入力された対数収益率の年次リターン・リスク（標準偏差）を月次へ変換
    self.mu_m = mu_y /12
    self.s_m = s_y / np.sqrt(12)
  • 引数として入力された年あたりの対数収益率の平均・標準偏差を月あたりへ変換し、格納します。

2. 投資期間、試行回数に応じた数の対数収益率に相当する乱数を生成

class asset_model
    def run_mc(self, dur_y, n):
        #入力された投資期間を年→月へ変換
        dur_m = dur_y * 12
        # [(投資期間_月),(試行回数)]の正規分布N(μ,σ)に従う乱数行列として毎月の対数収益率を生成
        A1 = np.random.normal(self.mu_m, self.s_m,size=[dur_m,n])        
        #次元を拡張し、[(投資期間_月),(投資期間_月),(試行回数)]の行列とする
        A2 = np.tile(A1,[dur_m,1,1])
        #行列を転置し、[(試行回数),(投資期間_月),(投資期間_月)]の行列とする
        A3 = np.transpose(A2,(2,0,1))
        #各試行の上三角行列を取得
        A4 = np.triu(A3)
        #計算結果を格納
        self.A = A4
        self.dur_m = dur_m
        print("Monte Carlo Calculation of "+ str(dur_y) + " years finished")
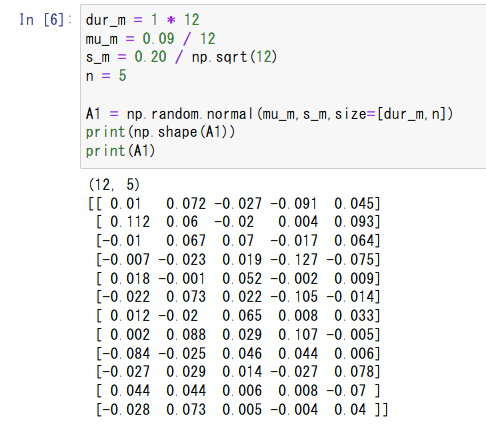
  • A1 = np.random.normal(self.mu_m, self.s_m,size=[dur_m,n])
    前段で計算した平均mu_m、標準偏差s_mに従う正規分布の乱数行列を作成します
    行列のサイズは[投資期間_月,試行回数]となります
  • 以下、投資期間1年(dur_m=12）、試行回数n=5の例を示します
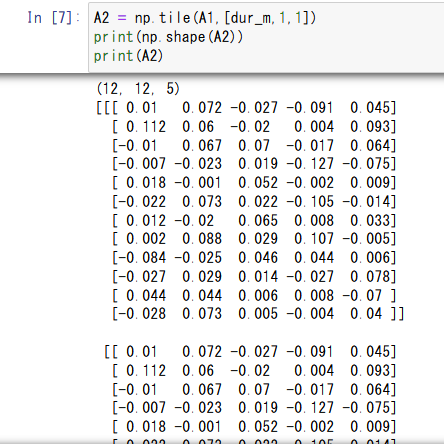
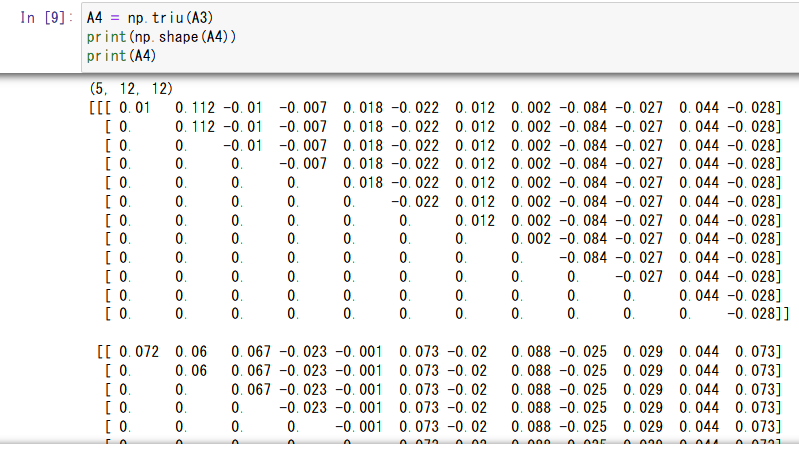
    image.png
  • A2 = np.tile(A1,[dur_m,1,1])
  • A3 = np.transpose(A2,(2,0,1))
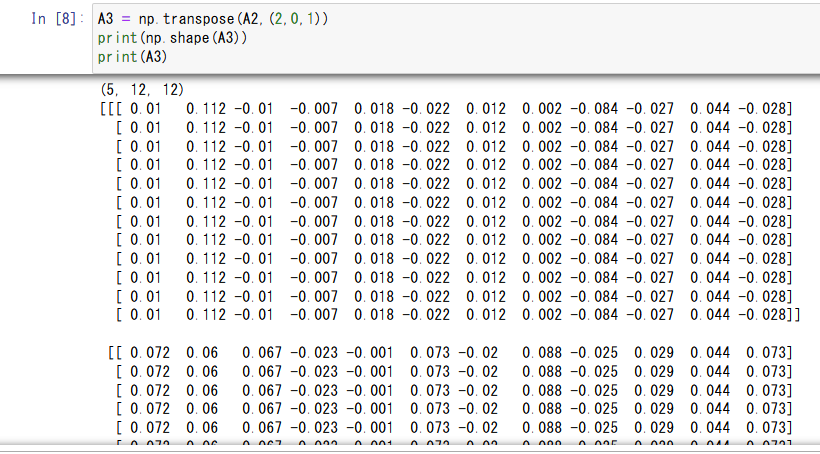
  • A4 = np.triu(A3)
    それぞれ、行列に以下のような変形操作を加え、最終的に[試行回数,投資期間 _月,投資期間_月]の形状の上三角行列を得ます。
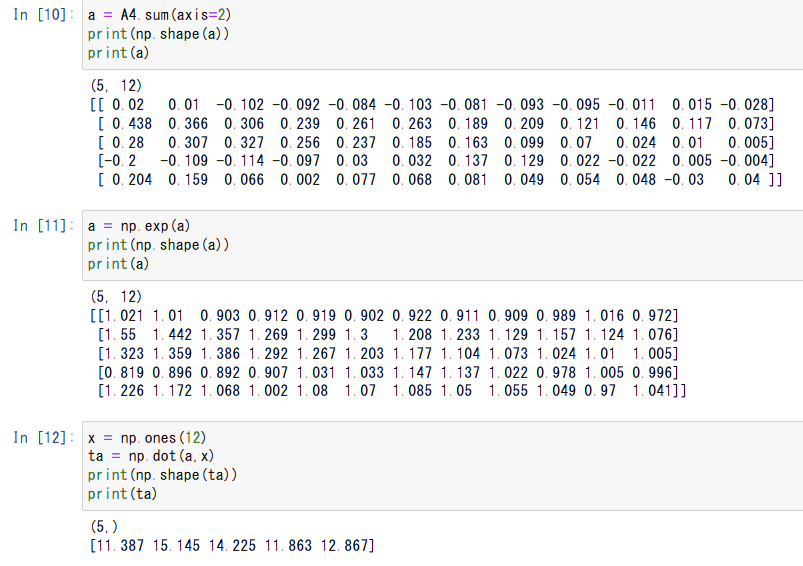
    image.png
    image.png
    image.png

3. 投入資金の、各時点における推移を計算

class asset_model
def exercise(self, x_init, delta_m):
    #月別の投資額のリスト
    x = delta_m * np.ones(self.dur_m)
    #初期投資額を追加
    x[0] = x[0] + x_init
    
    #総資産額のリスト
    ta_list = []
    #累計投資額のリスト
    capital = [] 
    
    #総資産額の推移を1年毎(12ヶ月毎)に集計する
    for i in range(11, self.dur_m,12):
        #集計時点までの対数収益率行列を切り出し
        A_tmp = self.A[:,:i+1, :i+1] 
        #集計時点までの投資額のリストを切り出し
        x_tmp = x[:i+1]
        #対数収益率行列の各行の和を計算
        A_tmp = A_tmp.sum(axis=2)
        #対数収益率から、価格変動比へ変換
        A_tmp = np.exp(A_tmp)
        #各試行の、投資期間経過後の資産額を計算
        ta = np.dot(A_tmp,x_tmp)
        #計算結果を格納
        ta_list.append(ta)
        
        #累計投資額を格納
        capital.append(x_tmp.sum())
  • 以下、投資期間1年(dur_m=12）、試行回数n=5の例の続きです。
  • 前段で得られた上三角行列は、$i$ヶ月目の月次の対数収益率を$lr_i$とすると、次のように表されます。
\boldsymbol{A}=
\begin{bmatrix}
lr_1 & lr_2&  \dots & lr_{12} \\\  
0 &lr_2&\dots & lr_{12} \\\ 
\vdots & \vdots & \ddots & \vdots \\\ 
0 & 0 & \dots & lr_{12} \\\ 
\end{bmatrix}
  • 行列$\boldsymbol{A}$の各行を足して、さらに指数関数を掛けて得られる列ベクトル$\boldsymbol{a}$と、各月の積立投資額の列ベクトル$\boldsymbol{x}$の内積を計算することで、$t=12$の総資産額$TotalAsset_t$を求めています。
\boldsymbol{a}=
\begin{bmatrix}
\exp (lr_1+\dots+lr_{12}) \\\  
\exp (lr_2+\dots+lr_{12}) \\\ 
\vdots \\\ 
\exp (lr_{12}) \\\ 
\end{bmatrix} \quad
\boldsymbol{x}=
\begin{bmatrix}
X_0\\\  
X_1\\\ 
\vdots \\\ 
X_{11}\\\ 
\end{bmatrix}

\begin{align}
TotalAsset_{12} &= \boldsymbol{a} \cdot \boldsymbol{x} \\\
&= X_0 *\exp (lr_1+\dots+lr_{12})+\dots+X_{11}*\exp(lr_{12})
\end{align}
  • 実際の計算処理上は、これにモンテカルロ法の試行回数の次元（例ではn=5)が加わります。
  • 以下の例では、各月の積立額は簡単のためX=1としています。
    image.png

4. 計算結果を出力

def exercise(続き）
    #1年毎の各種統計値を計算
    #平均
    mean = np.mean(ta_list, axis=1)
    #パーセンタイル値（np.percetileは下位○%を入力するが、出力としては上位○%の表記とする）
    p10 = np.percentile(ta_list,90,axis=1)
    p25 = np.percentile(ta_list,75,axis=1)
    p50 = np.percentile(ta_list,50,axis=1)
    p75 = np.percentile(ta_list,25,axis=1)
    p90 = np.percentile(ta_list,10,axis=1)
    
    year = np.arange(self.dur_m/12)+1
    
    #計算結果をDataFrameに格納
    df_result = pd.DataFrame(np.transpose([year,mean,p10,p25,p50,p75,p90,capital]),columns=["Year","Mean","P10","P25","P50","P75","P90","Capital"])
    pd.options.display.float_format = '{:.1f}'.format
    display(df_result)
        
    #グラフ出力
    left, width = 0.1, 0.65 
    bottom, height = 0.1, 0.65 
    fig_main = [left, bottom, width, height] #散布図の定義
    fig =plt.figure(figsize=(10,7)) 
    ax = fig.add_axes(fig_main)
    
    ax.fill_between(df_result["Year"],df_result["P10"],df_result["P90"], alpha=0.3, label="Range P10-P90")
    ax.fill_between(df_result["Year"],df_result["P25"],df_result["P75"], alpha=0.3, label="Range P25-P75")
    ax.plot(df_result["Year"],df_result["P50"], label="P50")
    ax.plot(df_result["Year"], df_result["Capital"], label="Capital")
    ax.set_ylim(0, max(df_result["P10"])*1.1)
    ax.set_xlim(1,max(df_result["Year"]))
    ax.set_xlabel("Year")
    ax.set_ylabel("Total assets")
    ax.grid(True)
    ax.legend()
  • 計算結果の平均や各種パーセンタイル値を整理した上で、matplotlibを用いて図化しています
104
128
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
104
128