Q#を触ってみた

12月11日にMicrosoft Researchが公開したQ#という量子プログラミング言語を触ってみたので、以下に紹介します。量子コンピューティングの基礎も含めて説明してみます。

Visual Studio 2017のインストール

Microsoft Visual Studio Downloadにアクセスし、Community版をインストールする。既にVisual Studio 2017をインストールしている方は不要です。

Visual Studio 2017へのインストール

1. Quantum Computingにアクセスして、Download Nowをクリックする。
2. 使用者情報の入力を求められるので入力してDownload Nowをクリックする。
3. Visual Studio 2017用のnsixのダウンロードが開始する。ダウンロードしたQSharpVSIX.vsixをクリックしてVS2017にインストールする。

Q#サンプルプロジェクトのclone

1. プルダウンメニューの「チーム(M)」をクリックし、「接続を管理(M)」を選択する。
2. 右側の「チームエクスプローラー」タブをクリックし、ローカルGitリポジトリの下の「複製」(git clone)を選択し、アドレス欄に「https://github.com/Microsoft/Quantum.git」を入力した後に、「複製」ボタンを選択する。
3. ローカルリポジトリに「Quantum」が表示されるので、それをダブルクリックする。すると、ソリューションに「QsharpLibraries.sln」が表示されるので、同様にダブルクリックする。

以上により、ソリューションエクスプローラーにQSharpLibrariesが展開される。QsharpLibrariesには種々の量子アルゴリズムのサンプルプロジェクトが格納されています。内容は以下のとおりです。

Introduction

TeleportationSample

量子テレポーテーションのサンプルプロジェクトです。EPRペアにした二つのqubitの片方及びある状態をAliceに渡し、EPRペアのもう片方をBobに渡して、Alice側の二つのqubitを測定した結果に基づいて、Bob側のqubitにXゲート及びZゲートを作用させることで、とある状態をテレポーテーションさせるものです。No-cloning theoremにより、qubitの複製は禁止なので、複製ではありません。

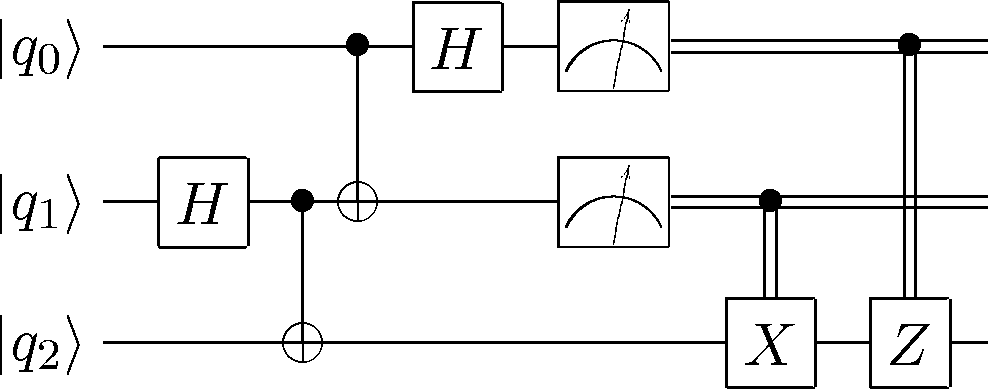
量子テレポーテーションの量子回路

Teleport.qs

// msg：Aliceが送信するテレポートさせるqubit、there:Bobが受信するqubit
operation Teleport(msg : Qubit, there : Qubit) : () {
        body {

            using (register = Qubit[1]) {
                // EPRペアを作成するためのqubitを用意します。
                let here = register[0];

                // 用意したqubitにHadamardゲートを作用させ、制御NOTを作用させることで量子もつれのEPRペアを作り出します。hereをAlice, thereをBobに渡します。
                H(here);
                CNOT(here, there);

                // テレポートさせるqubitとhereに制御NOT、アダマールゲートを作用させます。
                CNOT(msg, here);
                H(msg);

                // Aliceがテレポートさせるqubitを観測して1の場合、Bobに渡したqubitにZゲートを作用させます。
                if (M(msg) == One)  { Z(there); }
                // AliceがEPRペアの片方のhereを観測して1の場合、さらにBobに渡したqubitにXゲートを作用させます。
                if (M(here) == One) { X(there); }

                // hereをリセット(|0>にする)します。
                Reset(here);
            }
        }
    }

Measurement

重ね合わせ状態となったqubit(2^(-1/2)|0> + 2^(-1/2)|1>)に対して測定を行うプロジェクトが含まれています。

SimpleAlgorithm

以下の3つの量子アルゴリズムのサンプルプロジェクトが含まれています。

1. パリティ演算を実施するBernstein-Viziraniのフーリエサンプリングアルゴリズム(Ethan Bernstein and Umesh Vazirani*, SIAM J. Comput., 26(5), 1411–1473, 1997)

2. 関数がバランス型か定数型を判別するDeutcsh-Jozsaのアルゴリズム(David Deutsch and Richard Jozsa (1992). "Rapid solutions of problems by quantum computation". Proceedings of the Royal Society of London A. 439: 553. )

3. Bent関数の隠れシフト問題を解くための相関アルゴリズム(Martin Roetteler, Proc. SODA 2010, ACM, pp. 448-457, 2010)

Algorithm

データベース探索に威力を発揮するGroverのアルゴリズム、素因数分解に威力を発揮するShorのアルゴリズムのプロジェクトが含まれています。

DatabaseSearchSample

Factoring

Characterization and Testing

量子誤り訂正のための3桁ビットフリップコード(Error Correction)、ベイジアン位相推定(Krysta M. Svore,1, Matthew B. Hastings, and Michael Freedman. "Faster Phase Estimation")、Fredkinゲート等の単体試験のプロジェクトが含まれています。

Simulation

水素の量子シミュレーション(O'Malley et. al. Scalable Quantum Simulation of Molecular Energies)、Ising模型のシミュレーション、Hubbard模型のシミュレーションが含まれています。

LibraryTest

Q# Standard Libraryのテストが揃っています。

Microsoft.Quantum.Canon

Q# Standard Libraryの構成部品であるThe Canonが格納されています。The Preludeはターゲットマシンに対応した実装となりますが、The Canonはターゲットマシンに依存しません。

Further Reading

Microsoft Researchによる参考文献集です。

Nielsen, M. A. & Chuang, I. L. (2010). Quantum Computation and Quantum Information. Quantum Computation and Quantum Information, UK: Cambridge University Press, 2010.

Kitaev, A. Y., Shen, A., & Vyalyi, M. N. (2002). Classical and quantum computation (Vol. 47). Providence: American Mathematical Society.

Kaye, P., Laflamme, R., & Mosca, M. (2007). An introduction to quantum computing. Oxford University Press.

Rieffel, E. G., & Polak, W. H. (2011). Quantum computing: A gentle introduction. MIT Press.

制御ゲート(controlled-NOT, controlled-X等)の構築のための基礎

Barenco, A., Bennett, C. H., Cleve, R., DiVincenzo, D. P., Margolus, N., Shor, P., ... & Weinfurter, H. (1995). Elementary gates for quantum computation. Physical review A, 52(5), 3457.

Jones, C. (2013). Low-overhead constructions for the fault-tolerant Toffoli gate. Physical Review A, 87(2), 022328

量子状態の用意のための技術

Shende, V. V., Markov, I. L., & Bullock, S. S. (2004). Minimal universal two-qubit controlled-NOT-based circuits. Physical Review A, 69(6), 062321.

Ozols, M., Roetteler, M., & Roland, J. (2013). Quantum rejection sampling. ACM Transactions on Computation Theory (TOCT), 5(3), 11.

Grover, L., & Rudolph, T. (2002). Creating superpositions that correspond to efficiently integrable probability distributions. arXiv preprint quant-ph/0208112.
Farhi, E., Goldstone, J., Gutmann, S., & Sipser, M. (2000). Quantum computation by adiabatic evolution. arXiv preprint quant-ph/0001106.

量子回路の同期のためのアプローチ

Kliuchnikov, V., Maslov, D., & Mosca, M. (2013). Asymptotically optimal approximation of single qubit unitaries by Clifford and T circuits using a constant number of ancillary qubits. Physical review letters, 110(19), 190502.

Ross, N. J., & Selinger, P. (2014). Optimal ancilla-free Clifford+ T approximation of z-rotations. arXiv preprint arXiv:1403.2975.

Kliuchnikov, V. (2013). Synthesis of unitaries with Clifford+ T circuits. arXiv preprint arXiv:1306.3200.

Jones, N. C., Whitfield, J. D., McMahon, P. L., Yung, M. H., Van Meter, R., Aspuru-Guzik, A., & Yamamoto, Y. (2012). Faster quantum chemistry simulation on fault-tolerant quantum computers. New Journal of Physics, 14(11), 115023.

量子演算のためのアプローチ

Takahashi, Y., & Kunihiro, N. (2005). A linear-size quantum circuit for addition with no ancillary qubits. Quantum Information & Computation, 5(6), 440-448.
Draper, T. G. (2000). Addition on a quantum computer. arXiv preprint quant-ph/0008033.

Soeken, M., Roetteler, M., Wiebe, N., & De Micheli, G. (2017, March). Design automation and design space exploration for quantum computers. In 2017 Design, Automation & Test in Europe Conference & Exhibition (DATE) (pp. 470-475). IEEE.
Methods for fast quantum sampling (amplitude ampli cation) and probability estimation

Brassard, G., Hoyer, P., Mosca, M., & Tapp, A. (2002). Quantum amplitude amplification and estimation. Contemporary Mathematics, 305, 53-74.
Grover, L. K. (2005). Fixed-point quantum search. Physical Review Letters, 95(15), 150501.

Berry, D. W., Childs, A. M., & Kothari, R. (2015, October). Hamiltonian simulation with nearly optimal dependence on all parameters. In Foundations of Computer Science (FOCS), 2015 IEEE 56th Annual Symposium on (pp. 792-809). IEEE.
Algorithms for quantum simulation

Lloyd, S. (1996). Universal Quantum Simulators. Science (New York, NY), 273(5278), 1073.

Berry, D. W., Childs, A. M., Cleve, R., Kothari, R., & Somma, R. D. (2015). Simulating Hamiltonian dynamics with a truncated Taylor series. Physical Review letters, 114(9), 090502.

Low, G. H., & Chuang, I. L. (2017). Optimal Hamiltonian simulation by quantum signal processing. Physical Review letters, 118(1), 010501.
Low, G. H., & Chuang, I. L. (2016). Hamiltonian simulation by Qubitization. arXiv preprint:1610.06546.

Reiher, M., Wiebe, N., Svore, K. M., Wecker, D., & Troyer, M. (2017). Elucidating reaction mechanisms on quantum computers. Proceedings of the National Academy of Sciences, 201619152.

Wiebe, N., Berry, D. W., Høyer, P., & Sanders, B. C. (2011). Simulating quantum dynamics on a quantum computer. Journal of Physics A: Mathematical and Theoretical, 44(44), 445308.

Peruzzo, A., McClean, J., Shadbolt, P., Yung, M. H., Zhou, X. Q., Love, P. J., ... & Obrien, J. L. (2014). A variational eigenvalue solver on a photonic quantum processor. Nature communications, 5.
Procedures for quantum optimization

Durr, C., & Høyer, P. (1996). A quantum algorithm for finding the minimum. arXiv preprint quantph/9607014.

Farhi, E., Goldstone, J., & Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028.

Brandao, F. G., Svore, K. M. (2017). Quantum Speed-ups for Semidefinite Programming. In Annual Symposium on Foundations of Computer Science (FOCS 2017).

感想

既にいろいろある量子プログラミング言語QCL, Quipper, Qutip, QASM等に比べて、VSIXで一発で入るので導入が容易だと思いました。QuipperはWindows上で動かすためにMSYSやCabalで複数のパッケージを導入しなければならない頬か、QutipはJupyterのConda環境と実Python環境の食い違いでエラーが多発して大変でした。ただし、QutipやQuipperではブロッホ球や量子回路を出力できますが、これはできません。