追記
ELUとの比較を追加しました、金子さんのアイデアの凄さが明確に結果に出ています。
また最後にニューロンが正・負どちらに発火しているのか可視化したチャートも追加しました。
初めに
誤差逆伝播法を用いずに、興奮性・抑制性ニューロンの出力を調整することでニューラルネットワークの学習を進める金子さんの誤差拡散法はとても衝撃的でした。
しかし、誤差拡散法は現在広く使用されているニューラルネットワークのアーキテクチャとは互換性がないため、
今すでに利用されているニューラルネットワークに興奮性、抑制性ニューロンのアイデアを直接反映できません。
そのため、今の誤差逆伝播法の範囲内で興奮性・抑制性ニューロンの挙動を再現することを目的に新しい活性化関数ExPと改良型ExP2を作成しました。MINISTでのテストの結果、想像より良い性能が出たので公開します。
ExP(指数確率関数)の基本設計
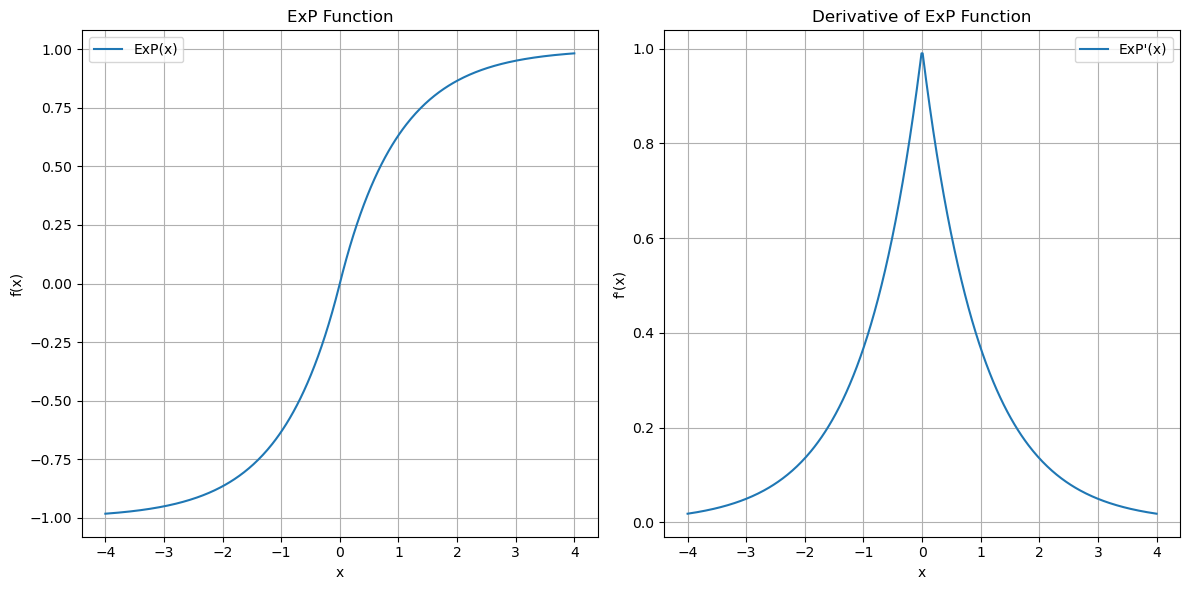
ExPの基本の数式はこちらです。
ExP(x)=sign(x)(1-e^{-|x|})
これは指数関数に、入力xの絶対値をとり、符号を-にした値を代入して0〜1までの数字に
変換、1から指数関数の結果を引き算して最後にsign(x)でxの符号を復元する関数です。
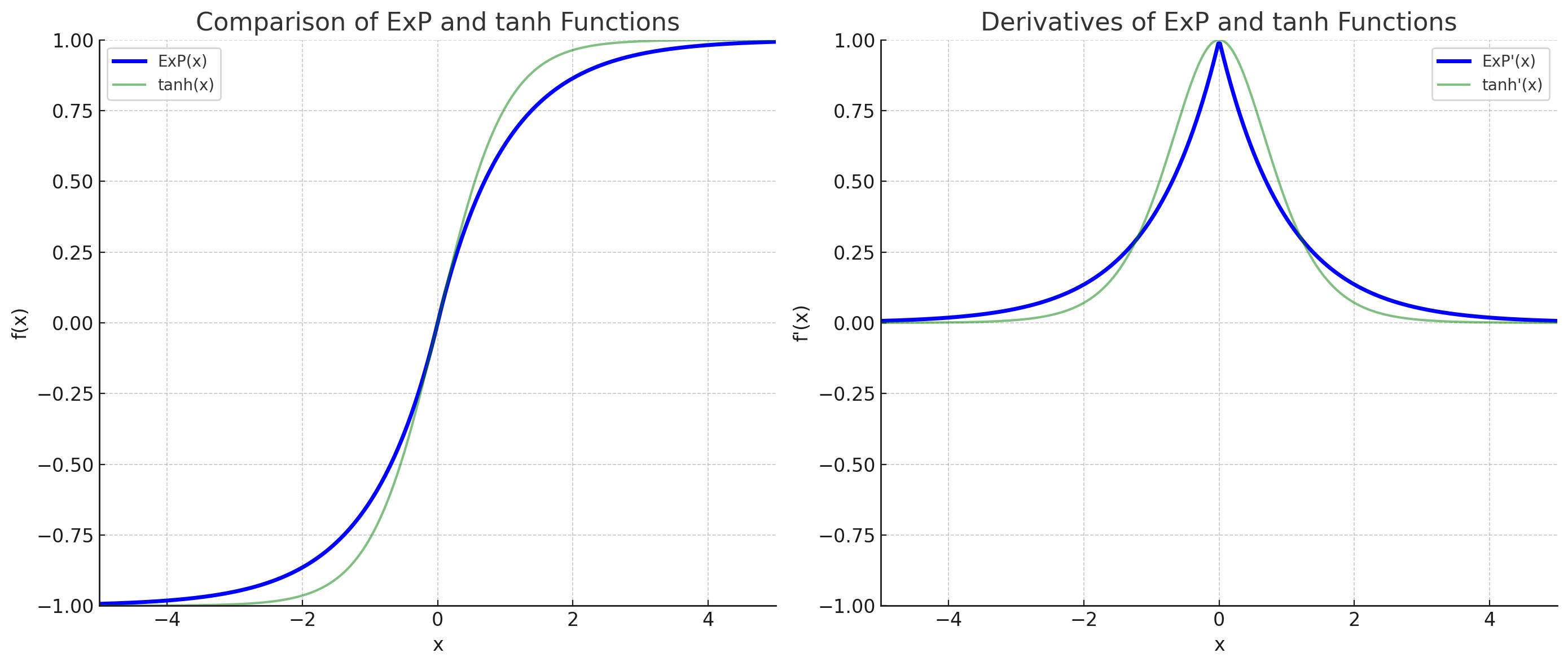
関数の出力はtanhと似ていますが、tanhと比較して0付近の勾配が急になっています。
関数の出力と微分値
ExPのコンセプト
この関数の目的は、ニューロンの出力を3値に収束させるように学習させることです。
すでに実績のある誤差逆伝播法を元にしたニューラルネットワークで興奮性・抑制性のニューロンがどのように機能しているのか可視化することを目指します。
また学習済モデルの解釈性を高めるために、
条件付き確率の計算をニューラルネットワークに学習させることを設計の基本としています。
ニューロンの発火確率の計算
まず、最初に3つのニューロンA,ニューロンB,ニューロンCを考えます。
ニューロンA、ニューロンBの出力はニューロンCの入力に接続されています。
ニューロンA、ニューロンBが共に発火した場合のニューロンCの発火確率は、
下記の式で求められます。
P(C∣A=1,B=1)=1-(1-P(C∣A=1))\times (1-P(C∣B=1)))
この式をニューラルネットワーク上で近似することを目的とします。
Ⅰ.
まず、計算を簡単にするため両辺に-1を掛けて、右辺の1を左辺に移動します。
1-P(C∣A=1,B=1)=(1-P(C∣A=1))\times (1-P(C∣B=1)))
A,Bが共に発火したときにCが発火しない確率=1-P(C∣A=1,B=1)
Ⅱ.
次に、これをニューラルネットワークで処理するために、自然対数を取ります。
\ln(1-P(C∣A=1,B=1))=\ln(1-P(C∣A=1))+\ln(1-P(C∣B=1))
Ⅲ.
最後に自然対数からExP関数を使用して逆変換します。
P(C∣A=1,B=1)=ExP(\ln(1-P(C∣A=1,B=1)))
ExP関数は入力xを自然対数から元の値に戻して1から引く関数のため
P(C∣A=1,B=1)=1-(1-P(C∣A=1,B=1))
最終的にExP関数の戻り値はA,Bが共に発火したときにCが発火する確率になります。
P(C∣A=1,B=1)
実際のニューラルネットワークではこんな感じの式になります。
\ln(1-P(C∣A=1,B=1))=A_{output}\times\ln(1-P(C∣A=1))+B_{output}\times\ln(1-P(C∣B=1))
この式が成り立つのはニューロンの出力が(1,0-1)のときだけです。
ニューロンの出力が0.693等半端な値の場合、誤差が大きくなります。
この誤差がニューロンの出力を正則化する方向に働いてくれるのであれば、ニューロンの出力が3値に収束するのではないかと期待しています。
接続重みについても、誤差逆伝播法で条件つき確率の補数の自然対数へと収束させることができれば、ニューロン間の接続状況を確率として可視化できるのではないかと考えています。
勾配消失問題への対処
ExP関数の出力のグラフはtanhとかなり似ています。
ExP関数のコンセプトがもし正しければ、近い応答をするtanhにも効果が現れるはずなのですが、
現実は勾配消失が起こらないRelu系の活性化関数の天下になっています。
実際ExP関数をテストしたところ、層が深くなると学習が上手くできませんでした。
ExP2(指数擬確率関数)
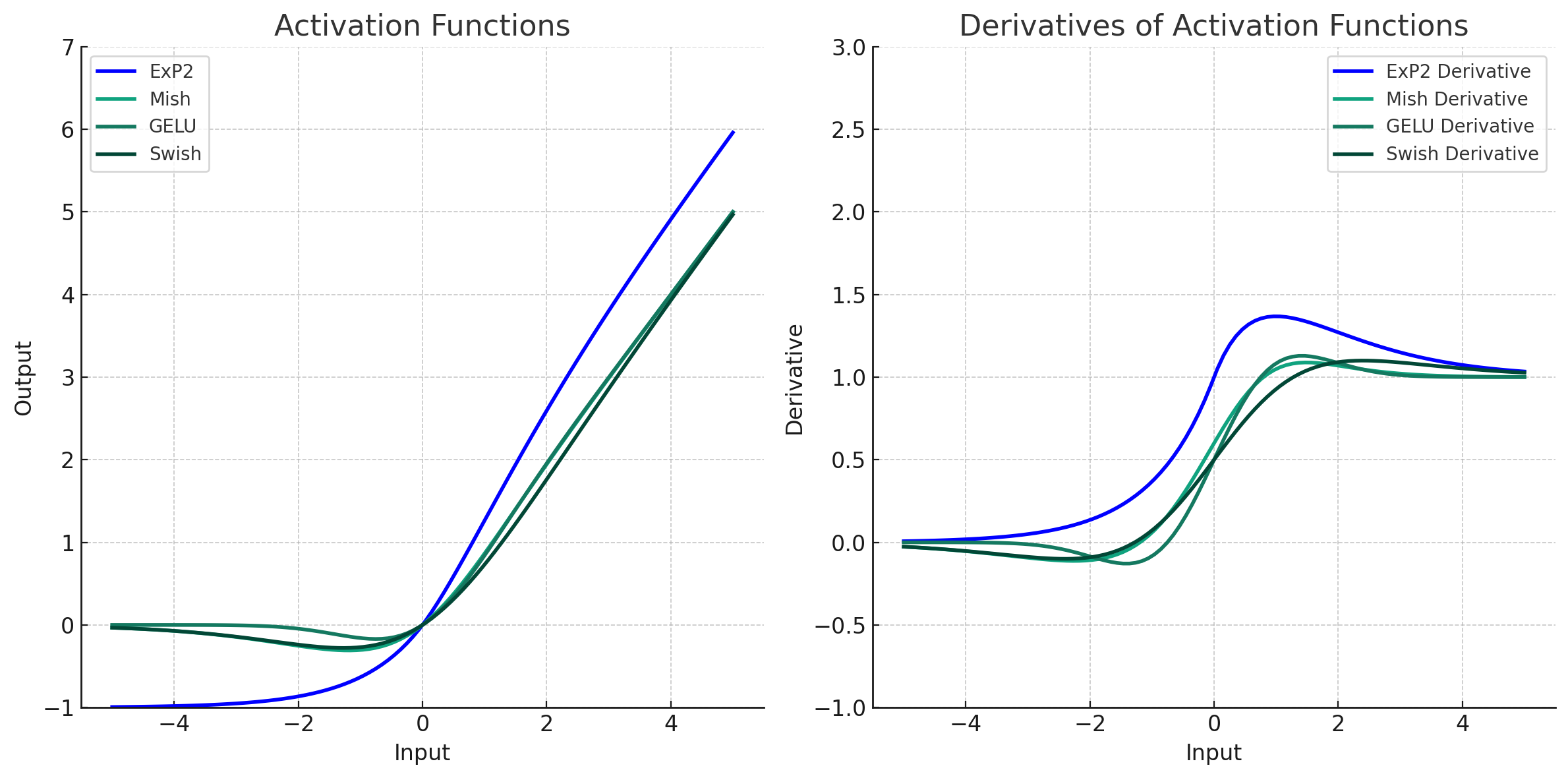
勾配消失問題に対応した改良版のExP2関数がこちら。
このExP2関数は、
負の入力にはExP関数と同じ応答
正の入力にはGELUやSwith等のRelu系改良型の活性化関数に近い応答をします。
1,0等の正規化されたデータに対する学習では、正の入力に対して線形に近い応答することで精度高くなる傾向があったため、正の入力に対して線形に近い応答をする設計を行っています。
正の方向に非線形があると学習初期に勾配消失が起こりやすくなるのではないかと考えています。
また負の入力のときに確率的応答を行うため、
負確率を出力する関数という意味で名称をExP2 指数擬確率(Exponential Pseudo Probability)としました。
ExP2関数の定義は以下の通り。正の入力に対して線形に応答する項目を追加しています。
- ( x >=0 )の場合:
ExP2(x) = +(1 - e^-x) \cdot (1 + x)
- ( x < 0 )の場合:
ExP2(x) = -(1 - e^{x})
あとは実際に、ニューラルネットワークで条件付き確率を計算するというコンセプトが成り立つのか検証した結果です。
MINSTデータセットでの性能比較
検証するのは、この4パターン
| 活性化関数 | オプティマイザー |
|---|---|
| ExP2 | SGD |
| ExP2 | Adam |
| GELU | SGD |
| GELU | Adam |
使用したモデルのコード
# CNNモデルの定義
class MinstCNN(nn.Module):
def __init__(self, activation_fn):
super(MinstCNN,self).__init__()
#畳み込み層
self.conv1 = nn.Conv2d(1, 32, kernel_size=5, padding=2)
self.conv2 = nn.Conv2d(32, 64, kernel_size=5, padding=2)
#全結合層 18層
self.fc1 = nn.Linear(64 * 7 * 7, 1024)
self.fc2 = nn.Linear(1024, 512)
self.fc3 = nn.Linear(512, 512)
self.fc4 = nn.Linear(512, 512)
self.fc5 = nn.Linear(512, 512)
self.fc6 = nn.Linear(512, 512)
self.fc7 = nn.Linear(512, 512)
self.fc8 = nn.Linear(512, 512)
self.fc9 = nn.Linear(512, 512)
self.fc10 = nn.Linear(512, 512)
self.fc11 = nn.Linear(512, 512)
self.fc12 = nn.Linear(512, 512)
self.fc13 = nn.Linear(512, 512)
self.fc14 = nn.Linear(512, 512)
self.fc15 = nn.Linear(512, 512)
self.fc16 = nn.Linear(512, 512)
self.fc17 = nn.Linear(512, 512)
self.fc18 = nn.Linear(512, 512)
#出力層
self.fc19 = nn.Linear(512, 10)
self.activation = activation_fn
self.pool = nn.MaxPool2d(2, 2)
def forward(self, x):
##略
モデル構成は下記になります。
| 畳み込み層 | 全結合層 | 出力層 | トータル | パラメータ数 |
|---|---|---|---|---|
| 2層 | 18層 | 層 | 21層 | 773万 |
MNISTを学習させるにはかなり過剰なモデルですが、
新しく線形応答を追加したことで勾配消失問題への対処が可能になったのかを検証するために巨大なモデルを使用しています。
MINSTデータセットでの検証結果
| 活性化関数 | オプティマイザー | テストデータでの最高精度 (%) | 最高精度のエポック数 |
|---|---|---|---|
| ExP2 | SGD | 99.43 | 48 |
| ExP2 | Adam | 99.07 | 77 |
| GELU | SGD | 11.35 | 0 |
| GELU | Adam | 98.44 | 75 |
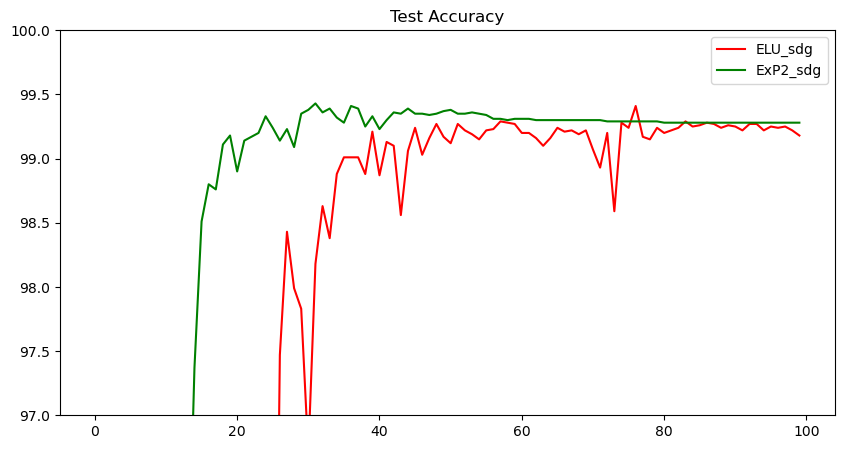
ExP2とSDGの組み合わせが99.43%で最高精度となりました、
モデルサイズと比較して学習データ少ないこともあり、過学習や学習できない可能性もありましたが、
特に問題なく学習ができています。
精度は48エポックの時点の99.43%が最高です。
11エポックまでは全く訓練ロスが下がらず、学習に失敗しているように見えますが。
訓練ロスが下がり始めた12エポック以降は、精度が向上しその後も安定して学習ができています。
後半は過学習の傾向が出てきていますが、テストデータへの精度は安定して99.37%あたりをキープしており、過学習への耐性があるように見えます。
その代わり、活性化関数自体に正則化効果があるため、Adamとは相性が良くないようです。
追記 ELUとの比較
ExP2とかなり近い活性化関数にELUがあります。

両関数とも負の値では全く同じ応答をします、ExPとの差異はELUは正の値では純粋に線形の応答をすることです。
これはELUがReLUの派生であり、正の値で線形応答することに重点をおいているからではないかと思います。
ExP2とELUの性能比較がこちらです。
| 活性化関数 | オプティマイザー | テストデータでの最高精度 (%) | 最高精度のエポック数 |
|---|---|---|---|
| ExP2 | SGD | 99.43 | 31 |
| ELU | SGD | 99.41 | 76 |
特性が近いため最高精度はほぼ同等になるようです。だた学習速度についてはExP2が速い傾向があります。
学習の進行速度と学習の安定性については、ExP2がx=1のポイントに勾配のピークがあることでいい方向に効いているのではないかと思います。
さらに追記 正負発火率
こちらはExP2のニューロンがエポック毎に正負のどちらに発火したか集計したチャートです。
精度が向上するタイミングで負の方向に発火するニューロンが急増していることがわかります。
直感的なイメージとは違い、ニューラルネットワークで抑制性ニューロンとして機能しているのは、
正の方向に発火するニューロンなのかもしれません。
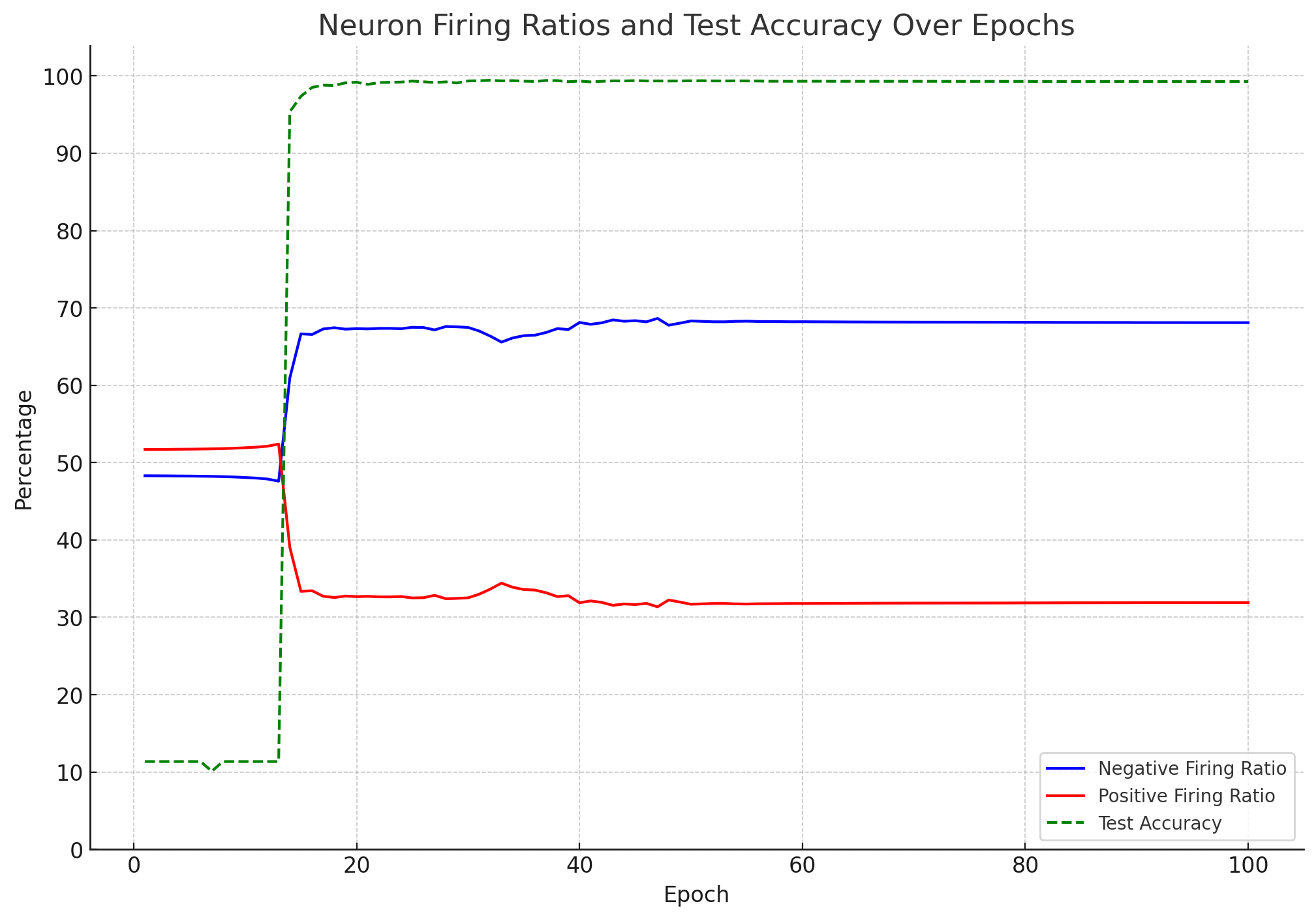
ちなみに、最大精度を記録した31エポックあたりでは負の方向に発火したニューロンの比率が66.3%です。
学習が進むと正:負 3:7の割合に近づいているように見えます。
モデル構造やデータによって比率は変わるかもしれません。
##検証に使ったカウンター付きの関数のコードです。
global_negative_count = 0
global_positive_count = 0
global_zero_count = 0
class TraceExP2(autograd.Function):
@staticmethod
def forward(ctx, x):
ctx.save_for_backward(x)
# マスクを計算
positive_mask = x > 0
negative_mask = x < 0
zero_mask = x == 0
# グローバルカウンタを更新
global global_negative_count, global_positive_count, global_zero_count
global_negative_count += negative_mask.sum().item()
global_positive_count += positive_mask.sum().item()
global_zero_count += zero_mask.sum().item()
# 順伝播の計算
y = (torch.sign(x) + torch.relu(x)) * (1 - torch.exp(-torch.abs(x)))
return y
@staticmethod
def backward(ctx, grad_output):
x, = ctx.saved_tensors
s = torch.sign(x)
pn = torch.relu(s)
rx = torch.relu(x)
ax = torch.abs(x)
cp = torch.exp(-ax)
grad_input = ((rx + 1) * cp + (pn - cp) * pn) * grad_output
return grad_input
まとめ
金子さんが考案したED法の興奮性・抑制性ニューロンのアイデアを誤差逆伝播法に適用することで、学習速度と安定性が向上することがわかりました、特にELUとの性能比較により、興奮性と抑制性のニューロンが存在することのメリットが明確にあらわれています。
1999年の時点で気づかれていた金子さんの先見性には本当に感服するばかりです。