プリミティブモデルを参考に、大気循環をシミュレーションしてみました。
シミュレーション条件が特殊だったり挙動が怪しい部分はありますが、一旦公開します。
コードはこちら。
結果
赤道(0°)付近が最も暖められて大気が上昇し、高緯度で下降する現象が再現できました。
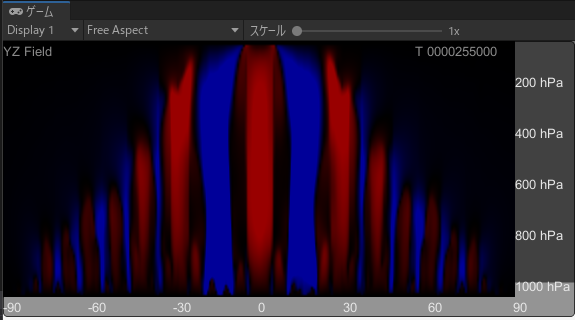
※赤は上昇、青は下降
シミュレーション条件
特殊な地球
- 地表の高低差は0(すべて海抜0m)
- 球ではなく、円筒(正距円筒図法。緯度が違っても1格子の面積は同じ)
プリミティブモデルをできるだけシンプルに適用
- 熱源は地表のみ
- 摩擦力なく、断熱大気
支配方程式
- 静力学平衡の式
\frac{\partial{p}}{\partial{z}} = -{\rho}{g}
- 運動方程式(摩擦力は無視)
\frac{du}{dt} = fv - \frac{\partial{gz}}{\partial{x}}
\frac{dv}{dt} = fu - \frac{\partial{gz}}{\partial{y}}
- 連続の式
\frac{\partial{u}}{\partial{x}} + \frac{\partial{v}}{\partial{y}} + \frac{\partial{w}}{\partial{p}} = 0
予測値の計算方法
- 気温T(K)
- 単純に、赤道から極にかけてsin分布で加熱します
- 地表付近の大気のみ加熱します
{dT} = sin(90°-\varphi)
- 標高Z(km)
Z = \int_{p_n}^{p_0}dz\\
{dz} = -\frac{1}{\rho{g}}{dp} = -\frac{RT}{g} \frac{dp}{p} = -\frac{RT}{g} d(\log{p})