「圏論勉強会第2回」資料を読んでたら「有界半束はモノイドである」というフレーズがあった。この辺りの Cats 実装を調べてみると、以下のような継承関係になっている。
この記事では有界半束BoundedSemilatticeを調べて実装してみる。前の記事に書いたPartialOrderも利用する。
使ってる技術など
Cats、Discipline、束論初歩と、Scalaのリフレクションを少々。
依存ライブラリ
- cats: 2.0.0-M1
- specs2: 4.3.6
- scalacheck: 1.14.0
(ソースはこちら)
有界半束
そもそも有界半束とは何か。馴染みがないのでWikipediaの束論のエントリと「順序集合と束」という離散数学の資料でしらべてみた。
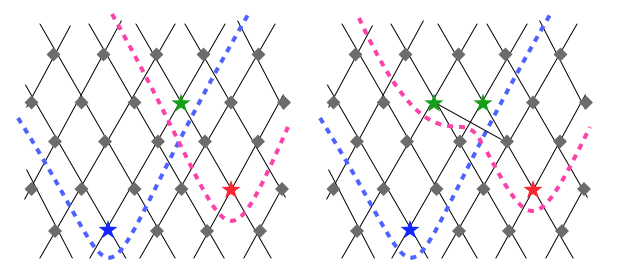
下の図のように、半順序集合内の比較可能な二つの要素を、大きい方を上にして線でつなげたとき、ある二つの要素から上向きに辿っていける領域の交差部分を上界という。
上界の中で最小のものがもしあればそれを結び(join)といい $a \lor b$ と表し、どの2つの要素をとっても結びがあるとき、この集合を結び半束 (join-semilattice) という。
向きを下にとった場合は、上界→下界、結び(join)→交わり (meet) ** $a \land b$、結び半束→交わり半束となる。また、結び半束かつ交わり半束であるものを束といい、最小要素と最大要素をもつ束のことを有界束**という。
図の左では、青と赤の上界に最小要素の緑が一つだけあり、これが結びとなる。ただし線を1本加えた図の右では、二つの緑のうちどちらが上界の最小か定まらないので結びがあるといえず、したがって右は半束にならない。
これらを踏まえて、Scala コードを書いてみる。
実装例
以降、traitの継承関係から半順序集合を作り、これを結びの有界半束として実装し、Disciplineで各種の法則に準拠しているか検証する。
半順序(PartialOrder)
以下のようにtraitを定義する。
trait A; trait B; trait C
trait D extends B; trait E extends B with C
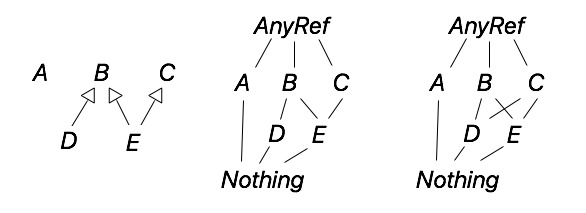
下図の左のような継承関係になる。
これらに共通の基底クラスとAnyRefと、結び半束の単位元となる最小元Nothingを加えると、上図中央のようなハッセ図になる。ちなみに、もしDがCをも継承していると上図右のようになり、DとEの結びがなくなるため有界半束にならない。
これらの型を半順序集合とするPartialOrderインスタンスを以下のように定義する。
implicit val typePartialOrder: PartialOrder[Type] = (x: Type, y: Type) =>
(x <:< y, y <:< x) match {
case (true, true) => 0.0
case (true, _) => -1.0
case (_ , true) => 1.0
case _ => Double.NaN
}
<:<はTypeApiで定義されていている演算子で、左辺の型が右辺の型に適合する(等しいか継承している)場合にtrueとなる。
半順序の法則を満たしているかどうか、以下のようにテストできる。
implicit def arbType: Arbitrary[Type] = Arbitrary(
Gen.oneOf(typeOf[Any], typeOf[A], typeOf[B], typeOf[C], typeOf[D], typeOf[E], typeOf[Nothing]))
private val checkTypePartialOrder = {
implicit val arbF: Arbitrary[Type => Type] = Arbitrary(Gen.const(t => t))
checkAll("型の半順序集合", PartialOrderTests[Type].partialOrder)
}
任意の型arbTypeはハッセ図上の型から一つ選択する。任意関数arbFは「相等性の代入原理」のチェックで使うが、この記事の内容とあまり関係がないので適当にした。
有界半束(BoundedSemilattice)
半順序集合になっていることが確認できたので、有界半束を実装してみる。BoundedSemilatticeのインスタンスを作るには、Semigroupで宣言されているcombineと、Monoidで宣言されているemptyを実装する必要があるが、それぞれ「結び」と最小値Nothingに対応づける。
implicit val typeBoundedSemilattice: BoundedSemilattice[Type] = new BoundedSemilattice[Type] {
val empty: Type = typeOf[Nothing]
def superTypesOf(t: Type): Set[Type] = t.baseClasses.map(t.baseType).toSet + t
def combine(x: Type, y: Type): Type =
if (x == empty) y
else if (y == empty) x else
(superTypesOf(x) intersect superTypesOf(y))
.toList
.sortWith((x, y) => x <= y) match {
case h :: Nil => h
case h1 :: h2 :: _ =>
assert((h1 tryCompare h2).nonEmpty, "結びがない!")
h1
}
}
Typeを得るためのtypeOfは、import scala.reflect.runtime.universe._で使えるようになる。結びの実装ではType#baseClassesで得た基底クラス集合の共通部分をPartialOrderで並べ替えて、先頭要素を返している。ただし、2番目の要素と比較不能な場合には、AssertionErrorを返すようにした。
これも Cats で提供されているルールを使って、Discipline で検証できる。
private val checkTypeBoundedSemilattice =
checkAll("型の有界半束", BoundedSemilatticeTests[Type].boundedSemilattice)
specs2で実行すると以下のような出力を得る。PartialOrderの部分は前回とかぶるので割愛した(コメントは後で書き足したもの)。
boundedSemilattice.associative // Semigroup law
boundedSemilattice.collect0 // Monoid law
boundedSemilattice.combine all // Monoid law
boundedSemilattice.combineAllOption // Semigroup law
boundedSemilattice.commutative // CommutativeSemigroup law
boundedSemilattice.idempotency // Band law
boundedSemilattice.is id // Monoid law
boundedSemilattice.left identity // Monoid law
boundedSemilattice.repeat0 // Monoid law
boundedSemilattice.repeat1 // Semigroup law
boundedSemilattice.repeat2 // Semigroup law
boundedSemilattice.right identity // Monoid law
Process finished with exit code 0
ためしにDがCも継承するようにしてから再テストすると、アサーションが失敗して”結びがない”旨のエラーメッセージが出力されることがわかる。
ちなみに、冒頭のBoundedSemilatticeそのものを含むクラス図も、AnyRefとNothingを加えるとそれ自身有界半束となり Discipline テストも成功する。
まとめ
やっぱり有界半束はモノイドだった