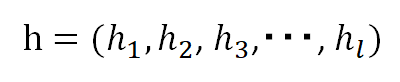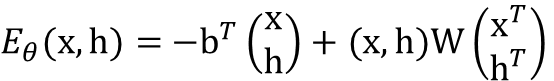量子コンピュータを機械学習モデル（ボルツマンマシン）で利用する方法（その１）

##はじめに

量子コンピュータ（D-wave)の活用方法の一つとして、ボルツマンマシンのトレーニングが「量子アニーリングの基礎 西森秀稔 大関真之【著】」の第10章に紹介されているのですが、私の統計力学および、ボルツマンマシンに対する予備知識が足りなかった為、これまで正直、消化不良の状態でした。最近になって、「ボルツマンマシン 恐神貴行【著】　コロナ社」や、D-wave Leapの「online learning」で知識を補充した結果、やっと私の頭の中で話が繋がってきました。かなり面白く感じたので、この感動が薄れないうちに、自分なりに纏めておこうと思います。
##対象とする読み手
ニューラルネットワークの学習（バックプロパゲーション）の仕組みをどこかで読んだことがあって、「へー面白いこと考えるなあ！」っていう感想を持ったことがある人で且つ「ボルツマンマシンってなに？」ぐらいな人には共感して頂けるかもしれません。

##ボルツマン機械学習とは
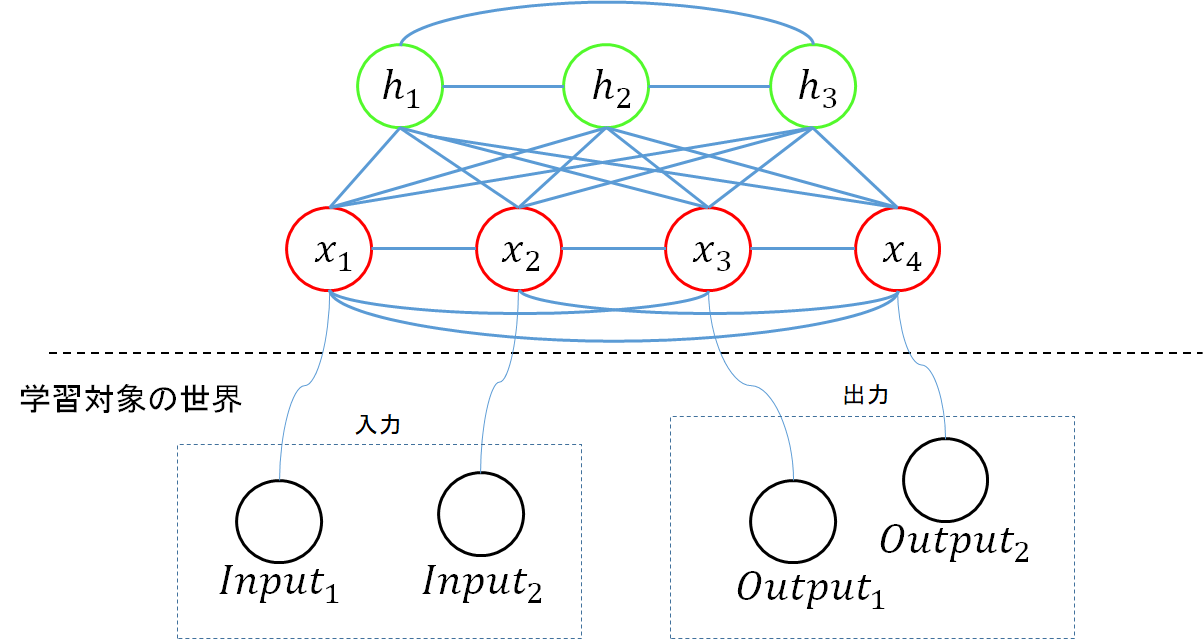
ボルツマンマシンは、ニューラルネットワークの一種です。こんな感じです。

上図は「ボルツマンマシン 恐神貴行【著】　コロナ社」を参考にしています。
赤い〇と緑の〇がユニットです。赤い〇は学習対象のパターンと対応するユニットで、可視ユニットと呼ばれます。緑の〇は学習対象のパターンとは直接対応しないユニットで隠れユニットと呼ばれます。なんかこのあたりは、普通のニューラルネットの入力層、隠れ層みたいな感じですね。黒い〇は、なんらか現実世界の事象を表すパターンで、0か1の値をとります。

ボルツマンマシンのパラメータとしては、ユニット間の結合の重みを示すパラメータωと、個々のユニットに設定されるバイアスbがあります。この辺も普通のニューラルネットワークと同じですね。
可視ユニットの値を、

隠れユニットの値を

、
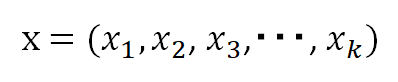
ユニット間の結合の重みωと、バイアスbを纏めて、パラメータθ

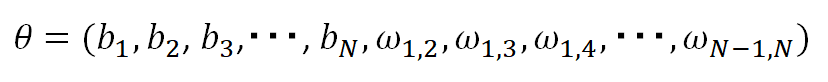
と表記すると、
ボルツマンマシンのエネルギーは、下記の式で定義されます。

上式のWは、ユニット間の結合の重みを保持している行列で、

（ただし　i<=jのとき、 ωi,j = 0）
です。また念の為書いておくと、$k+l = N$です

上記のようにエネルギーを定義すると、パラメータ$θ$で定義されるボルツマンマシンで、特定のx,hのパターンが発現する確率（確率分布の式）は、以下の式で与えられます。

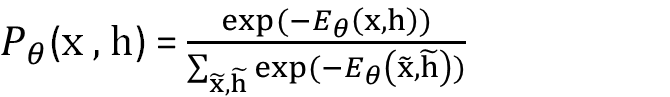
さて、ボルツマンマシンのエネルギーを定義し、確率分布を得ました。これでなにか面白いことができるのかというと、実際、面白いことができます。

xがなんらかの現実世界に存在するパターンだったとして、もしボルツマンマシンのパラメータ$θ$を調整することで、xの現実世界における確率分布をボルツマンマシンが生成する確率分布で近似できたならば、それを使って、現実世界のパターンを、現実世界で発現するような確率で生成することができるということになります。また、可視ユニットの一部を入力ユニットとし、一部を出力ユニットとして扱うことにすれば、ある特定の入力に対して、出力の確率分布がどのようになるか、予測できるということにもなります。下の図で言うならば、$x1$と$x2$を固定した上で、$x3$と$x4$の確率分布を求めれば、入力に対して、どのような出力が行われる可能性が高いのか、予測できる、ということになります。例えば、入力ユニットの数をもっと多く28x28個にして、出力ユニットを4個にして、MNISTのデータでトレーニングを行うなんてこともできるでしょう。

いいですね！ぜひ**$θ$**をうまく調整して、そういう機械学習モデルを手に入れたいものです。

では、どうやって$θ$すなわちバイアスbと重みωを調整するかというと、学習対象とする現実世界のパターンの確率分布と、$θ$で実現される確率分布の差が最少になるように調整していきます。二つの確率分布の差をKLダイバージェンスと呼ばれる量で計測し、このKLダイバージェンスが最少になるようにbとωを調整します。KLダイバージェンスを最小化することは、実は下記の関数$f$を最小化することとと同義です¹。

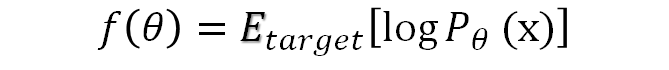
上式の$E_{target}[・]$は、近似対象の確率分布で期待値を取る事を意味します（この記事では、ここから先の$E$[・]は期待値の事であって、エネルギーではありませんので、ご注意ください²）。勾配降下で最小値を探す為に、この式の勾配を取ってみると、

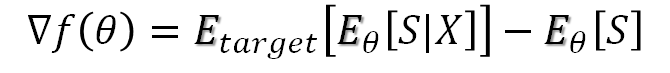
となります¹。ここで、$S$は、可視ユニットのベクトルxと隠れユニットのベクトルhを結合したベクトルです。第1項 $E_{target}[E_{\theta}[・|X]]$ は可視ユニットxの値を所与とした場合の、隠れユニットの期待値です。$E_{\theta}$[・]とは、ボルツマンマシンで算出される$P_{\theta}$に関する期待値です。
勾配が算出できれば、あとは勾配を降下して行けばよいのですが、困ったことに上の式には、期待値

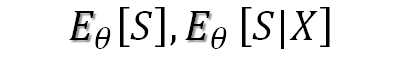
が含まれてしまっています。この期待値をまじめに取ろうとすると、$S$のすべてのパターンについて確率とSの積を取って加算しなければならず、これはSの次元が大きくなると非常に困難になります。
その為、MCMCベースの方法を用いて、期待値を近似的に算出し勾配降下を行っていくのですが、やはり近似値ですので、うまくいかないこともあるようです。
##量子コンピュータの利用
しかし、期待値算出の為のサンプリングをMCMCベースの方法ではなく量子コンピュータ(D-wave)で行うことで、より良い解に到達できるそうです！
下の図は、
Benchmarking Quantum Hardware for Training of Fully Visible Boltzmann Machines
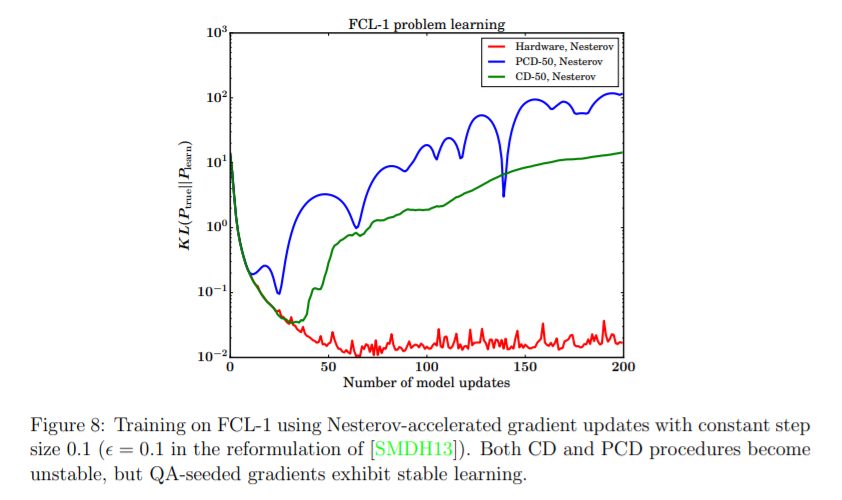からの抜粋です。縦軸がKLダイバージェンス、横軸が勾配降下の回数となっており、青と緑の線は、MCMCベースの方法、赤が量子コンピュータを利用した方法での勾配降下の様子です。この論文では、「隠れユニット無し」のボルツマンマシンを使用していて、勾配降下の式は、この記事で書いている式とはちょっと違い、

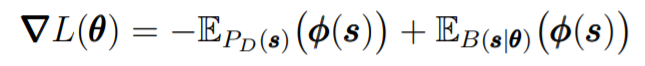
となっていますが、この式の右辺第2項は期待値の計算で、この計算をMCMCベースの方法で行った場合、KLダイバージェンスの値がうまく小さくなっていません。一方で、量子コンピュータの使用した勾配の計算により、よりよい解に到達していることが確認できます。

なんかほとんどボルツマンマシンの話になってしましました。次回は、D-wave Leapのonline learningに記載されている、制限ボルツマンマシン（RBM）のD-waveを用いたトレーニングにについて書こうと思います。

1. すみません、ものすごく途中をはしょっている自覚はあります。「ボルツマンマシン 恐神貴行【著】　コロナ社」で、丁寧に記述されていますので、詳細に興味がある方におすすめです。 ↩ ↩²

2. 期待値でよく使われる記号Eをどうやったら書けるのか誰かこっそり教えていただけないでしょうか。。 ↩