多重比較とは
前回の一元配置分散分析では、施肥に関して3つのグループの間に有意差があるかどうかを調べる方法を説明しました。しかし、一元配置分散分析の帰無仮説は3つ以上のグループ間に差がないということなので、どのペアの間に有意差があるかまではわかりません。そこで、どのペアの間に有意差があるかを知るには、それぞれのペアで検定を行う必要があります。これを多重比較と言います。また、多重比較も含め、統計検定を繰り返し行うような検定を多重検定と言います。多重検定には、他項目の2群比較なども含みます。
多重性の問題
すべての群間に差がない3水準データにおいて、3つのペアの比較(t検定)をそれぞれ有意水準5%で行うとします。この時にたまたま差を検出してしまう確率は 1 - 0.95×0.95×0.95 より約14%になります。つまり、たった3回の検定を繰り返すだけでも有意水準が14%近くに上がってしまうわけです。このように、統計検定を繰り返し行うことで、本当は有意差がないのに有意差があるとしてしまう第1種の過誤(Type I error)の確率が高くなってしまいます。この問題は多重性の問題と呼ばれ、未だに扱いの難しい課題となっています。そこで一般に、多重比較を行う時には検定ごとのp値を調整して一つ一つの有意水準を厳しく設定することで、第1種の過誤の抑え込みを図る必要があります。
有意水準の調整
ここでは詳しい説明は省略しますが、多重比較における代表的な有意水準(p値)の調整方法には大きく3つの考え方があります。一つは、全グループのデータのばらつきを元に、各群同士に差があるかを検定していく方法です。Tukey-Kramer法がこれに該当します。二つ目は、先述の「本当は差がないものの中から誤って一つでも差がある判定としてしまう確率(Familywise error rate) 」を5%などに調整する方法です。もとの有意水準を検定の回数で割って新たな有意水準とするBonferroni法などがこれに該当します。三つ目は、「差があると判定されたものの中で本当は差がない確率(False discovery rate, FDR)」を5%に設定する方法です。Benjamini and Hochberg法(BH法)がこれに該当します。Bonferroni法はp値の調整がシンプルですが、有意水準がかなり厳しいため検定数が増えると検出力が極端に落ちてしまうデメリットがあります。そのため、多重比較においては検出力の高いTukey-Kramer法が多く用いられます。一方、解析技術の発達によって機会の増えた遺伝子発現解析や微生物叢解析など、多項目の検定ではBH法が注目されています。
分散分析と多重比較の関係
「分散分析を行って有意差があった場合に多重比較を行う」というように多重比較を事後検定として扱う風潮もありますが、あまり正確な理解ではないように思います。例えば、多重比較の方法の中に分散分析と同じF検定が組み込まれているような方法(protected LSD, Scheffeなど)を用いる場合は、分散分析を行って有意差がなければ多重検定を行っても有意差は検出されません。しかし、一般的な多重比較法である先述のTukey-KramerやBonferroni法などにはF検定が組み込まれていないので、分散分析で有意差がなくても有意差が検出されることもありますし、分散分析で有意差があっても有意差が検出されないこともあり、多重比較の前手順としての分散分析の必要性は感じません。最初に述べたような風潮があるのは、protected LSDと呼ばれる事前の分散分析を前提とした方法の名残であるようですが、このprotected LSDではFamilywise error rateをコントロールすることができないので、4群以上の多重比較には不適切であるとされていて現在ではあまり使われていません。(参考:池田郁男,2013)
分散分析と多重比較を併用して良いか否かについても議論があります。その理由は、検定が増えることで新たに多重性の問題が生じるためです。そのため、多重比較を行う場合に、上記のprotected LSDなどのF統計量を用いる方法以外では分散分析は併用しない方が良いという考え方もあります。ただし、乱塊法でブロックの効果と処理の効果の大きさを比較することができるなどの分散分析による考察もできるので、トレードオフを理解して併用するかしないかを判断すれば良いかと思います。
解析方法
ここからはRを使って実際に多重比較を行っていきます。
0. データ
データは1要因5水準のデータを用意します。ここでは5段階の施肥量(N0,N10,N15,N20,N25)でコマツナを生育させたときの収量のデータを想定します。前回に倣い、乱塊法で3つのブロックを設置して、それぞれの区画から3つサンプルを取って平均しますが、最初からデータフレームを作ってしまっても良いと思います。データの詳細は一元配置分散分析のデータの説明を参照してください。
set.seed(2021)
v <- matrix(c(
c(rnorm(3, 20, 2),rnorm(3, 20, 2),rnorm(3, 21, 2)),
c(rnorm(3, 23, 2),rnorm(3, 23, 2),rnorm(3, 24, 2)),
c(rnorm(3, 27, 2),rnorm(3, 28, 2),rnorm(3, 28, 2)),
c(rnorm(3, 28, 2),rnorm(3, 29, 2),rnorm(3, 31, 2)),
c(rnorm(3, 25, 2),rnorm(3, 25, 2),rnorm(3, 25, 2))
),nrow=9)
b <- factor(c(rep("1",3),rep("2",3),rep("3",3)))
raw_data <- data.frame(b,v)
colnames(raw_data) <- c("block","N0","N10","N15","N20","N25")
library(tidyverse)
df <- raw_data %>%
pivot_longer(col = -block, names_to = "treatment", values_to = "value")
data <- df %>%
group_by(block,treatment) %>%
dplyr::summarise(yield = mean(value))
data$treatment <- as.factor(data$treatment)
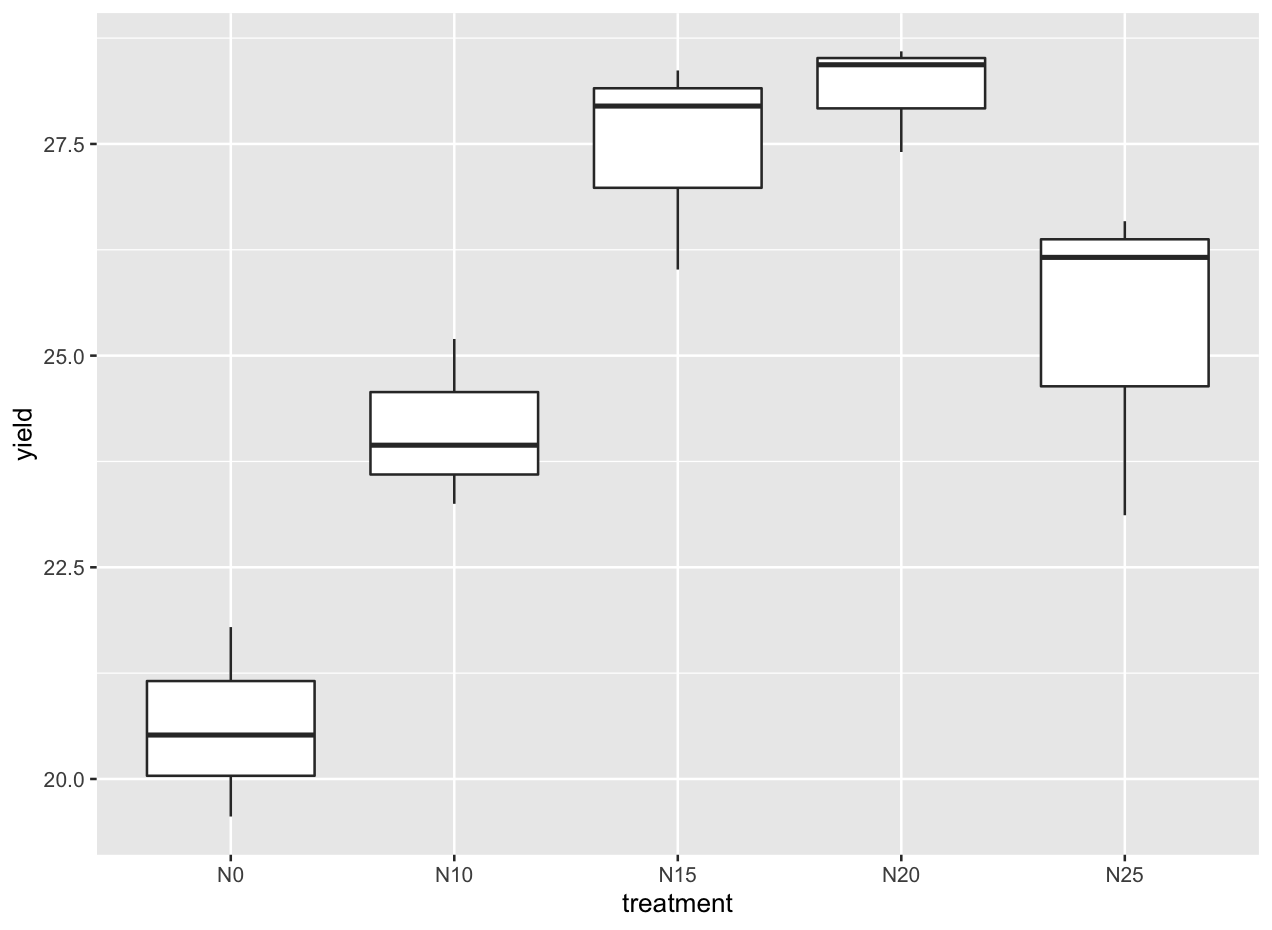
まずは、データを可視化して傾向を見てみます。
g <- ggplot(data, aes(x = treatment, y = yield))+
geom_boxplot()
g
グラフを見ると施肥の効果がよく見えます。 施肥量が N0 から N15 (kg/10a) まで増えるに従って収量が増加してぃす。N15 ~ N20 で頭打ちになり、N25 で少し減少しているような傾向があります。これらの関係を多重比較で確かめていきます。
2. 多重比較
それでは、多重比較を行っていきます。
2-0. 補正なし
まずはp値を補正せずに繰り返しt検定で比較を行った場合を考えてみます。
総当たりでt検定を行うには、Rにデフォルトで入っている pairwise.t.test() という関数が使えます。第一引数には値のデータを入れて、第二引数には処理のデータを入れます。そして第三引数では、補正の方法を指定します。「p.adj =」を書かなくても動きますが、今回は目立つように書いています。まずは補正なしの場合を見たいので "none" を指定してあげます。指定しないと何故かデフォルトのHolm法というFamilywise error rate の補正方法が適用されるので"none"が必要です。
pairwise.t.test(data$yield, data$treatment, p.adj = "none")
結果は以下の通りです。各検定のp値が行列の形で表示されます。なので、例えば一番左上の値はN0とN10を比較した時のp値となります。これらの結果は後で補正を行なった場合と比較してみます。
Pairwise comparisons using t tests with pooled SD
data: data$yield and data$treatment
N0 N10 N15 N20
N10 0.0064 - - -
N15 5.5e-05 0.0087 - -
N20 2.4e-05 0.0028 0.5079 -
N25 0.0010 0.2829 0.0607 0.0188
P value adjustment method: none
2-1. Tukey-Kramer法
Tukey-Kramer法ではBonferroniやBH法と異なり、P値の補正に平均や分散の値を用います。Rにデフォルトで入っているTukeyHSD()という関数が最も一般的です。
TukeyHSD(aov(data$yield ~ data$treatment))
結果は以下の通りです。pairwise.t.test()と少し結果の表示の仕方が違いますが、p adj(補正されたp値)などを見て結果を評価します。
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = data$yield ~ data$treatment)
$`data$treatment`
diff lwr upr p adj
N10-N0 3.5062931 0.14825123 6.8643349 0.0399002
N15-N0 6.8207676 3.46272579 10.1788095 0.0004068
N20-N0 7.5214129 4.16337106 10.8794547 0.0001802
N25-N0 4.6642914 1.30624961 8.0223333 0.0070756
N15-N10 3.3144746 -0.04356728 6.6725164 0.0534250
N20-N10 4.0151198 0.65707800 7.3731617 0.0184575
N25-N10 1.1579984 -2.20004346 4.5160402 0.7855272
N20-N15 0.7006453 -2.65739656 4.0586871 0.9549345
N25-N15 -2.1564762 -5.51451801 1.2015657 0.2859601
N25-N20 -2.8571215 -6.21516329 0.5009204 0.1064248
また、後々のグラフの描写のしやすさから、multcompというパッケージのglht()という関数を使う方法も紹介します。
# install.packages("multcomp")
library(multcomp)
res <- lm(yield ~ treatment, d=data)
tukey_res <- glht(res, linfct=mcp(treatment="Tukey"))
summary(tukey_res)
結果はTukeyHSD()を使用した場合と等しくなります。
Simultaneous Tests for General Linear Hypotheses
Multiple Comparisons of Means: Tukey Contrasts
Fit: aov(formula = yield ~ treatment, data = data)
Linear Hypotheses:
Estimate Std. Error t value Pr(>|t|)
N10 - N0 == 0 3.5063 1.0203 3.436 0.0399 *
N15 - N0 == 0 6.8208 1.0203 6.685 <0.001 ***
N20 - N0 == 0 7.5214 1.0203 7.371 <0.001 ***
N25 - N0 == 0 4.6643 1.0203 4.571 0.0070 **
N15 - N10 == 0 3.3145 1.0203 3.248 0.0534 .
N20 - N10 == 0 4.0151 1.0203 3.935 0.0185 *
N25 - N10 == 0 1.1580 1.0203 1.135 0.7855
N20 - N15 == 0 0.7006 1.0203 0.687 0.9549
N25 - N15 == 0 -2.1565 1.0203 -2.113 0.2859
N25 - N20 == 0 -2.8571 1.0203 -2.800 0.1064
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- single-step method)
2-2. Bonferroni
次にBonferroni法を適用します。やり方は簡単で、pairwise.t.test() の第三引数を**"bonf"**に変更します。
pairwise.t.test(data$yield, data$treatment, p.adj = "bonf")
Pairwise comparisons using t tests with pooled SD
data: data$yield and data$treatment
N0 N10 N15 N20
N10 0.06370 - - -
N15 0.00055 0.08744 - -
N20 0.00024 0.02797 1.00000 -
N25 0.01024 1.00000 0.60686 0.18790
P value adjustment method: bonferroni
2-3. BH法
最後にBH法です。pairwise.t.test() の引数に "BH" を指定します。
pairwise.t.test(data$yield, data$treatment, p.adj = "BH")
Pairwise comparisons using t tests with pooled SD
data: data$yield and data$treatment
N0 N10 N15 N20
N10 0.01274 - - -
N15 0.00027 0.01457 - -
N20 0.00024 0.00699 0.50790 -
N25 0.00341 0.31432 0.07586 0.02684
P value adjustment method: BH
結果を振り返ってみます。いずれの方法でも補正なしの時に比べてp値が総じて大きく計算されています。つまり、有意の判定が厳しくなっています。例えば、Bonferroni法の結果を見ると、補正されたp値は補正前のp値のちょうど10倍の値になっています。Bonferroni法では、10回の検定の各検定における有意水準は 0.05/10 になるので、p値を補正するには各値を10倍にすればいいということになります。
補正の厳しさを比較すると、今回の5群比較の例では Bonferroni > Tukey-Kramer > BH の順となっています。つまり、Tukey-Kramer法やBH法の検出力が高くなっています。例えばBonferroniでは有意差がなかった「N0 vs N10」「N10 vs N15」「N20 vs N25」の比較において、BH法では有意な結果になっています。
3. グラフ描写
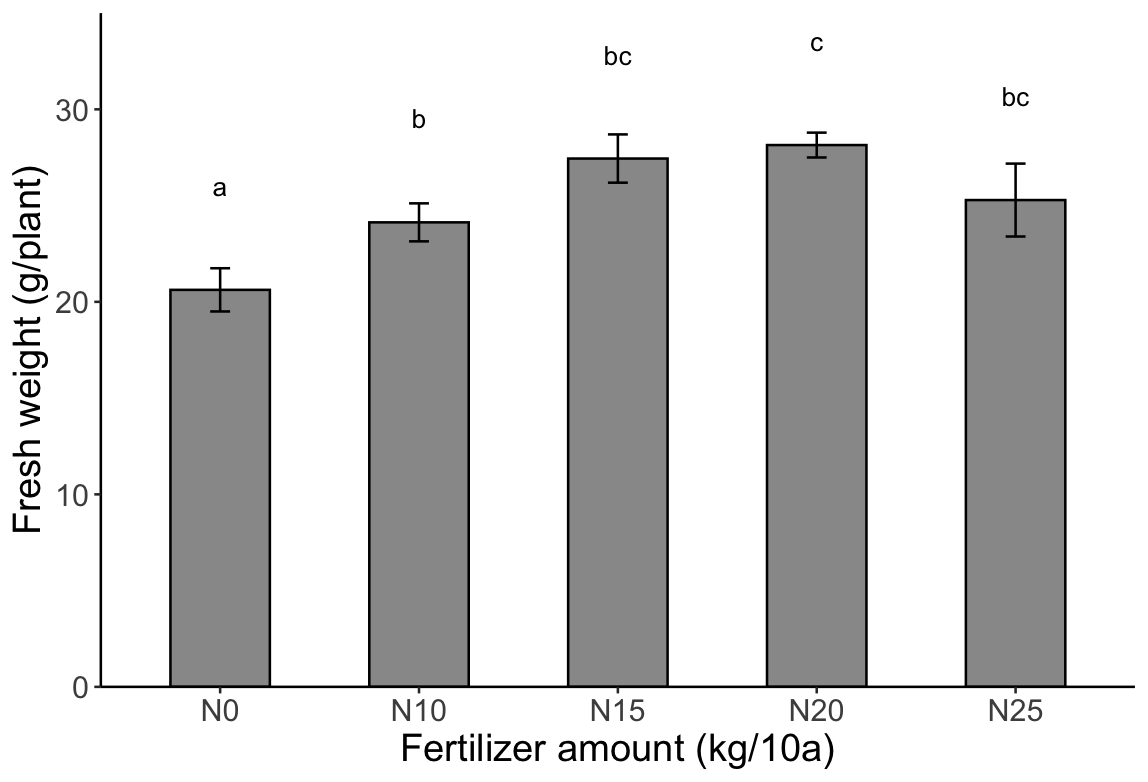
最後に結果をグラフにしてみます。Tukey-Kramerの結果を使って以下のような棒グラフを書いてみました。
まず、Tukey-Kramerの結果から有意差の記号を取り出します。ここでは、先程のmultcompパッケージのglht()の結果(tukey_res)を使用しました。
mltv = cld(tukey_res, decreasing=F)
annos = mltv[["mcletters"]][["Letters"]]
次に、棒グラフとエラーバーを作るために、処理ごとの平均および分散を算出したデータフレームを作成しておきます。
g_data <- data %>%
group_by(treatment) %>%
dplyr::summarise(average = mean(yield), sd = sd(yield))
グラフはggplotで描写します。それぞれのバーの上にある英字が有意差の有無を表現しています。同じアルファベットのもの同士は有意差がありません。また、bcがついているものは、bともcとも有意差がなかったことを表しています。
g <- ggplot(g_data, aes(x = treatment, y = average, fill = treatment))+
geom_bar(width = 0.5, stat = "identity", color = "black", show.legend = FALSE)+
geom_errorbar(aes(ymax = average + sd, ymin = average - sd), width=0.1)+
stat_summary(geom = 'text', label =annos, vjust = -5)+
scale_y_continuous(expand = c(0,0),limits = c(0,35))+
labs(x = "Fertilizer amount (kg/10a)", y = "Fresh weight (g/plant)")+
scale_fill_manual(values = rep("#999999", 5))+
theme_classic()+
theme(text = element_text(size=16))
g
以上で多重比較の解析は完了です。データの整形などでやや冗長なコードになっしまったかもしれませんが、最後に今回のコードを全てまとめて置いておきます。
4. 全てのコード
set.seed(2021)
v <- matrix(c(
c(rnorm(3, 20, 2),rnorm(3, 20, 2),rnorm(3, 21, 2)),
c(rnorm(3, 23, 2),rnorm(3, 23, 2),rnorm(3, 24, 2)),
c(rnorm(3, 27, 2),rnorm(3, 28, 2),rnorm(3, 28, 2)),
c(rnorm(3, 28, 2),rnorm(3, 29, 2),rnorm(3, 31, 2)),
c(rnorm(3, 25, 2),rnorm(3, 25, 2),rnorm(3, 25, 2))
),nrow=9)
b <- factor(c(rep("1",3),rep("2",3),rep("3",3)))
raw_data <- data.frame(b,v)
colnames(raw_data) <- c("block","N0","N10","N15","N20","N25")
library(tidyverse)
df <- raw_data %>%
pivot_longer(col = -block, names_to = "treatment", values_to = "value")
data <- df %>%
group_by(block,treatment) %>%
dplyr::summarise(yield = mean(value))
g <- ggplot(data, aes(x = treatment, y = yield))+
geom_boxplot()
g
result <- aov(yield ~ block + treatment, data = data)
summary(result)
# 補正なし
pairwise.t.test(data$yield, data$treatment, p.adj = "none")
# Bonferroni法
pairwise.t.test(data$yield, data$treatment, p.adj = "bonf")
# BH法
pairwise.t.test(data$yield, data$treatment, p.adj = "BH")
# Tukey-Kramer法
library(multcomp)
res <- lm(yield ~ treatment, d=data)
tukey_res <- glht(res, linfct=mcp(treatment="Tukey"))
summary(tukey_res)
mltv = cld(tukey_res, decreasing=F)
annos = mltv[["mcletters"]][["Letters"]]
g_data <- data %>%
group_by(treatment) %>%
dplyr::summarise(average = mean(yield), sd = sd(yield))
g <- ggplot(g_data, aes(x = treatment, y = average, fill = treatment))+
geom_bar(width = 0.5, stat = "identity", color = "black", show.legend = FALSE)+
geom_errorbar(aes(ymax = average + sd, ymin = average - sd), width=0.1)+
stat_summary(geom = 'text', label =annos, vjust = -5)+
scale_y_continuous(expand = c(0,0),limits = c(0,35))+
labs(x = "Fertilizer amount (kg/10a)", y = "Fresh weight (g/plant)")+
scale_fill_manual(values = rep("#999999", 5))+
theme_classic()+
theme(text = element_text(size=16))
g