一元配置分散分析 とは
分散分析とは、要因の異なる複数のグループの母平均に差があるか(=要因の効果がありそうか)を分析する手法です。特に、要因が1つである場合にとる分散分析を「一元配置分散分析(One-way ANOVA)」と呼びます。なので、2つの場合は二元配置分散分析(Two-way ANOVA)」になります。
大まかな手順としては、処理間(水準間)のばらつきと処理内(水準内)のばらつきの比からF値と呼ばれる統計量を計算し、得られたF値がF分布したがっていると仮定してp値を算出し、帰無仮説を判定します。実際のp値の算出手順は複雑なので、ここでは統計の詳しい内容は省略をして、具体的なデータを想定しながらRを使った一元配置分散分析を考えていくことにします。
一元配置分散分析を用いる実験の例
以下のような圃場実験を行った場合に、一元配置分散分析が使えます。
3種類の施肥量- N0、N10、N20 (kg/10a) -で栽培試験を行い、コマツナの糖度(Brix値)に違いがみられるかを調べる。
この実験での要因=**処理(Treatment)は窒素の施肥量のみです。ここでは、0kg、10kg、20kgの3種類の施肥量を設定しています。これらを水準(Level)**と呼びます。従って、これは1要因3水準のデータとなります。このデータを使って知りたいことは、3つの水準間で糖度に差があるかどうかということになります。
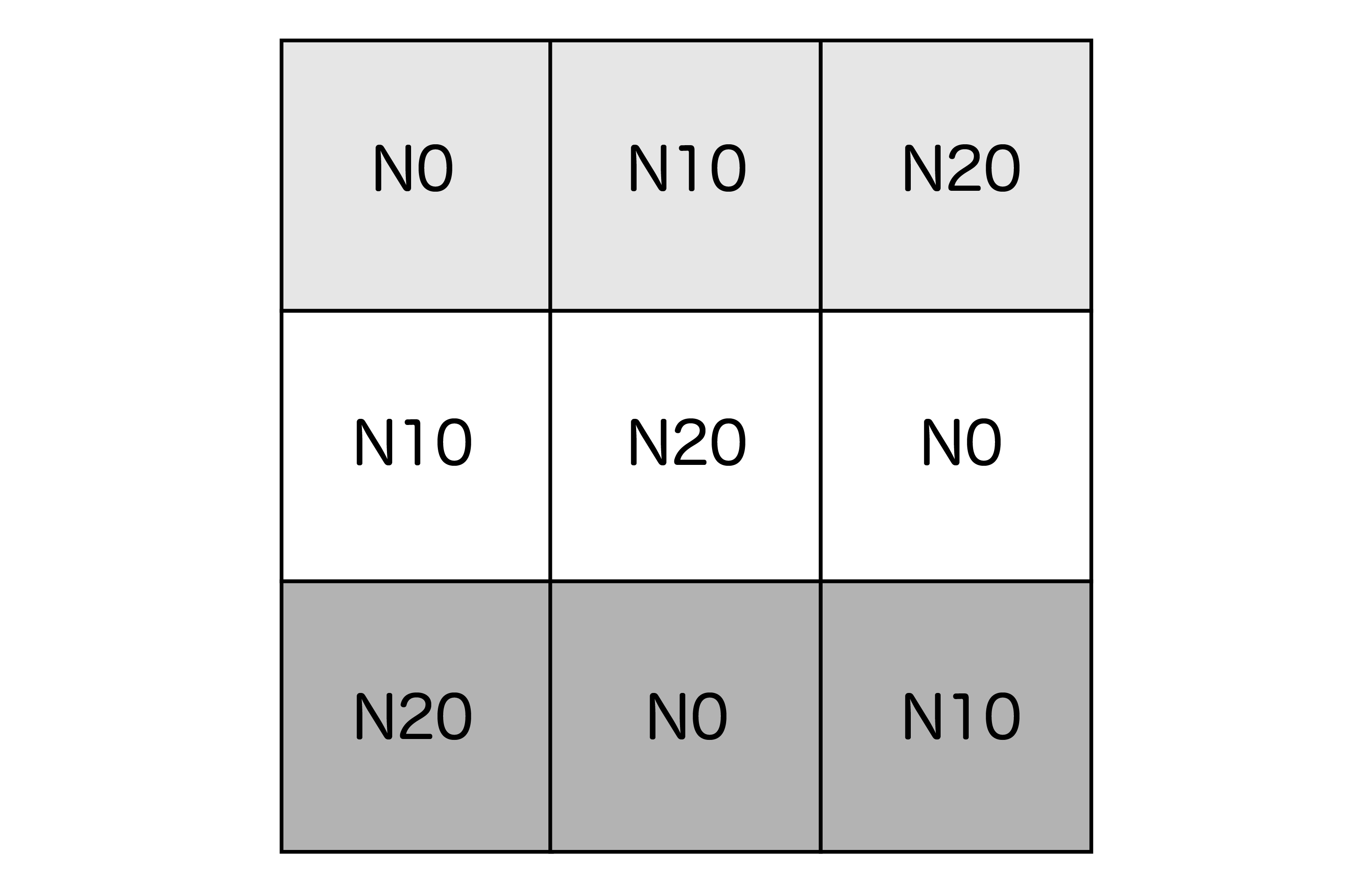
次に、この実験の圃場の配置も考えてみます。よく行うのは、以下のような配置です。
ここで注目したいのは、圃場全体を3つのブロック(上図の背景色に相当)に分けていることです。このようなデザインの方法を「乱塊法(Randomized block design)」と呼びます。
なぜこのようなことをするのかというと、一つの圃場内でも場所によって条件に差が生じる可能性があるためです。例えば、南北方向に傾斜があり南側ほど水はけが悪くなっている場合、南側のサンプルでは生育が悪かったりするかもしれません。
そこで乱塊法では次のようにします。まず、東西方向に畑を区切ってブロックを(通常3つ以上)設置します。このとき、東西方向と言ったのは、ブロック内の条件がなるべく均一になるようにブロックの配置を工夫するためです。そして、ブロックごとに反復を取り、各ブロック内ではランダムに処理を配置します。このような配置にすることで、場所によるデータのバイアスがなるべく小さくなるようにしています。これはFisherの三原則の中の「局所管理」の考え方に当たります。
この乱塊法では、ブロック間の差が顕著な場合に、同一処理のサンプル同士のばらつきが大きくなって処理の効果が検出されづらくなります。そこで、分散分析を行う際はブロックの効果を因子として入れる工夫をして、処理の効果とブロックの効果を分けて分析をしてあげることで、処理の効果が見えやすくなります。
今回の例では、3つのブロックを設置しています(反復 n=3)。そして、各プロットからは3つずつサンプルを取り、その平均値をプロットの値とすることにします。圃場試験ではこのような実験のデザインが一般的にとられています。
解析方法
ここから、実際にRを使った一元配置分散分析を行います。
1. データの準備
まず、上記の実験設定に沿って仮想の生データを作っておきます。ここは、実際に得られたデータに置き換えて見てみてください。
set.seed(2021)
v <- matrix(c(
c(rnorm(3, 5.0, 0.25),rnorm(3, 4.8, 0.25), rnorm(3, 4.5, 0.25)),
c(rnorm(3, 4.6, 0.25),rnorm(3, 4.2, 0.25),rnorm(3, 4.2, 0.25)),
c(rnorm(3, 4.4, 0.25),rnorm(3, 4.1, 0.25),rnorm(3, 3.9, 0.25))
),nrow=9)
b <- factor(c(rep("1",3),rep("2",3),rep("3",3)))
raw_data <- data.frame(b,v)
colnames(raw_data) <- c("block","N0","N10","N20")
上記のコードでは、平均が異なり分散が等しい正規分布を使ってデータを作っています。
もし手元のcsvファイルなどを読み込む場合は、以下のようにread.csv関数を用いて読み込みます。
raw_data <- read.csv(data.csv, header=TRUE)
ここでは、以下のようなデータを生データと想定しています。1列目にはブロックの番号(1〜3)を入れていて、2列目〜4列目にはそれぞれの水準のデータを入っています。
| block | N0 | N10 | N20 |
|---|---|---|---|
| 1 | 4.969385 | 5.032491 | 4.770281 |
| 1 | 5.138114 | 4.329449 | 4.778330 |
| 1 | 5.087162 | 4.531794 | 4.164389 |
| 2 | 4.889908 | 4.245499 | 4.053579 |
| 2 | 5.024513 | 4.577135 | 3.824719 |
| 2 | 4.319358 | 4.601118 | 4.402029 |
| 3 | 4.565436 | 3.739631 | 3.493765 |
| 3 | 4.728892 | 4.605828 | 3.926345 |
| 3 | 4.503443 | 4.232847 | 3.536139 |
このデータを、この後に使う関数に渡しやすいような形に変形しておきます。tidyverseというパッケージ集の中のtidyrというパッケージのpivot_longerという関数を使うと簡単です。以前はreshapeというパッケージのmelt()という関数がよく用いられていました。
# install.packages("tidyverse")
library(tidyverse)
df <- raw_data %>%
pivot_longer(col = -block, names_to = "treatment", values_to = "value")
できたデータフレームは以下のような形で、1列目にはブロックの番号(1〜3)、2列目には処理のカテゴリ(N0・N10・N20)、3列目にはBrixの測定値が入っています。
上記コードについて詳しくはこちら
tidyverse とは複数の便利なパッケージをまとめたパッケージ集です。これをインストール・読み込みすることで、データ解析に役立つモダンなパッケージを一括でインストール・読み込んでくれます。
ここでやりたいことは、生データの列名でもあるN0・N10・N20を変数として扱い、それに合わせてBrixの値も一列にまとめ、縦に長いデータデータフレームを作ることです。こうすることで、その後の解析で用いる馴染んだデータフレームになります。こういった変形を行うパッケージや関数は色々ありますが、tidyverseに含まれるtidyrというパッケージのpivot_longerという関数が現状では一番有用視されているように思います。ここでいうピボットとは、横長のデータをフレームを縦長に展開するような操作を指しています。
まず、上記のコードの %>% の部分は、tidyverse(dplyr)に入っているパイプ演算子と呼ばれるものです。これは、前のデータ(raw_data)を後ろの関数(pivot_longer)に引き渡す、という意味を持っています。
pivot_longerの引数の col は、ピボットしたい列を入れますが、ここではマイナスをつけて動かしたくない列(ブロックの列)を指定する形にしています。names_to にはもともと列名だったもの(処理)を入れる列の名前を決めてあげて、values_to では値(Brix値)を入れる列の名前を決めてあげます。すると以下のようなデータフレームに変化します。
> df
# A tibble: 27 × 3
block treatment value
<fct> <chr> <dbl>
1 1 N0 4.97
2 1 N10 5.03
3 1 N20 4.77
4 1 N0 5.14
5 1 N10 4.33
6 1 N20 4.78
7 1 N0 5.09
8 1 N10 4.53
9 1 N20 4.16
10 2 N0 4.89
# … with 17 more rows
いま各プロットで3つのサンプルをとってきたことを想定しているので、3水準×3反復×3サンプル=合計27サンプル(27行)になっています。ここで、同一プロット内のサンプルを別データとして扱ってしまうと、擬似反復にあたり統計的に正しくないと解釈されてしまいます。そこで、一元配置分散分析を行う前に、各プロットのデータの平均しておきます。こういったグループごとの計算は、tidyverseを読み込んだ時に自動的に読み込まれるdplyrというパッケージのgroup_byという関数を使うと便利です。
data <- df %>%
group_by(block,treatment) %>%
summarise(brix=mean(value))
結果、以下のようなデータフレームができあがりました。3サンプルずつ平均値をまとめたので、今度は9行のデータになっています。
上記コードについて詳しくはこちら
dplyrは、データフレームの操作や集計に特化したパッケージで、tidyversの中に含まれています。dplyrはC++で書かれているため、計算の実行速度が速いという特徴があります。
group_by は文字通りグルーピングを行う関数です。上記のコード2行目では、データフレーム(df)をブロックと処理の組み合わせて9つのグループに分けています。これを%>%でsummariseという関数に渡しています。summariseという関数は集計用の関数で、ここではmean(平均)の集計を行なってbrixという列名の列に格納しています。この際に、先ほどグルーピングを行なっていたので、グループごとに平均を計算しています。各ブロックの各処理、つまりここでは各プロットの3つのサンプルの平均を計算しています。
> data
# A tibble: 9 × 3
# Groups: block [3]
block treatment brix
<fct> <fct> <dbl>
1 1 N0 5.06
2 1 N10 4.63
3 1 N20 4.57
4 2 N0 4.74
5 2 N10 4.47
6 2 N20 4.09
7 3 N0 4.60
8 3 N10 4.19
9 3 N20 3.65
これでデータの準備は完了しました。dplyrの扱いに慣れないなという場合は、エクセル上でここまで作っておいてもよいと思います。
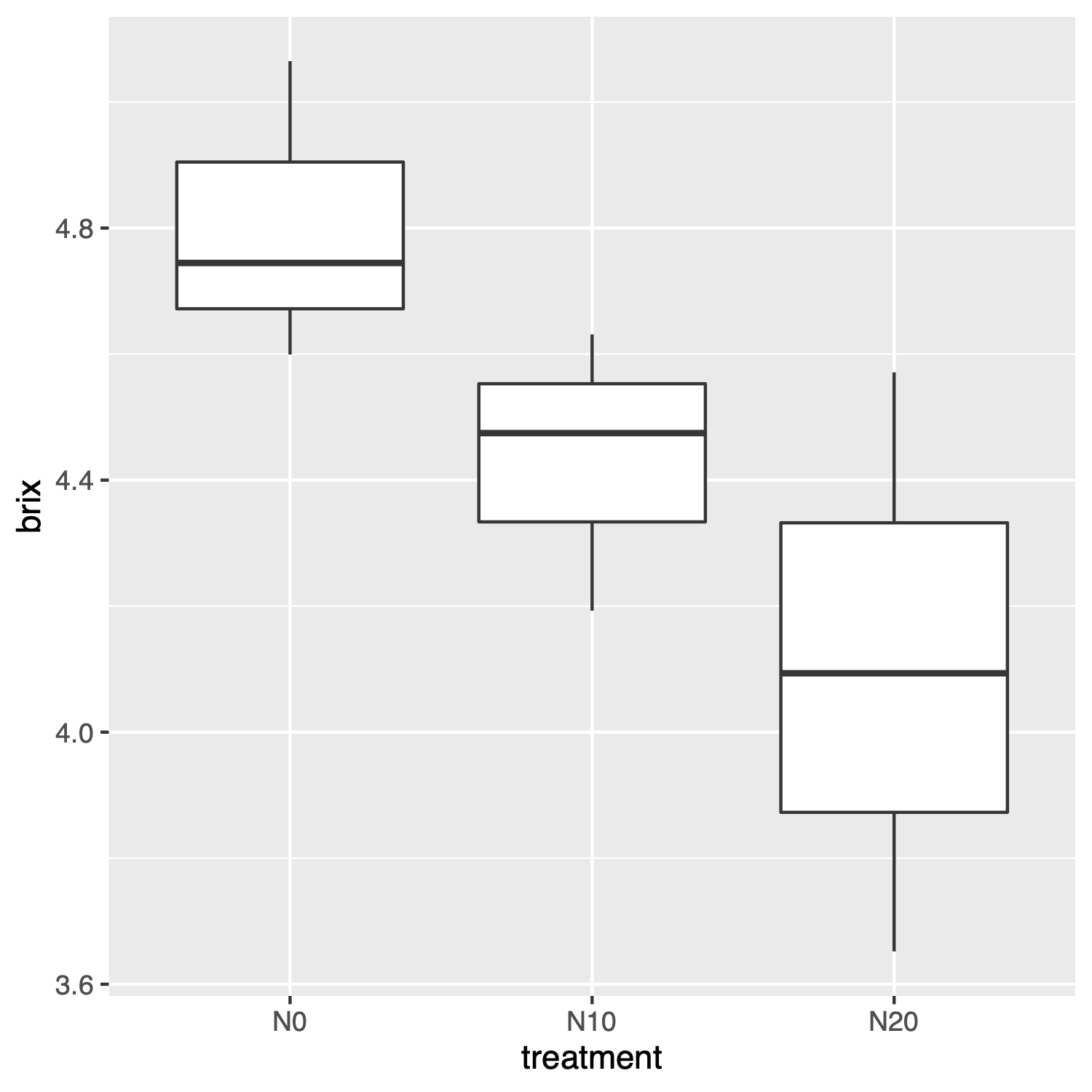
さて、一元配置分散分析の前にこのデータを可視化しておきます。データ解析の前にデータの傾向を把握しておくことも大事なステップだと思います。そこで、先程のtidyverseを読み込んだ時に自動的に読み込まれるggplot2というパッケージで箱ひげ図を描いて、処理ごとの傾向を見ておきます。傾向を見るだけなので見た目には拘らず簡単に描いてみます。
g <- ggplot(data, aes(x = treatment, y = brix))+
geom_boxplot()
g
上記コードについて詳しくはこちら
ggplot2はグラフ描写用のパッケージです。Rにデフォルトで入っているplot関数でも箱ひげ図等を描くことができますが、ggplot2はよりモダンで汎用性の高い描写ツールになっていて、色々とカスタマイズをするのには便利です。これもtidyversのパッケージ群に含まれています。
1行目では、まずグラフ描写を行うデータを指定した上で、x軸とy軸にあたる変数をaes()内で指定しています。ggplotでは上記のプラス記号を使ってオプションを追加していくような書き方をします。2行目では、指定したデータを箱ひげ図にするために、geom_boxplotという関数を利用しています。これらをgという変数に格納したので、3行目でそれを実際にプロットする流れになります。グラフはRStudioのPlotタブに自動で表示されます。
このグラフを見ると、N0で最もBrixが高く、N20で最も低くなっているように見えます。そこで、統計的に見て本当に差があるかどうかを一元配置分散分析を使って確かめていきます。
2. 乱塊法に基づく一元配置分散分析
分散分析は、aov関数という関数を用いて1行で実行できます。
result <- aov(brix ~ block + treatment, data = data)
上記コードについて詳しくはこちら
aovの括弧内の書き方は、モデル構築に共通の書き方です。
「~」記号の前に目的変数(従属変数)、後ろに説明変数(独立変数)を入れます。上記のように複数の説明変数を入れることもできます。それらを「+」で繋いだ場合は交互作用を考慮しないモデル、「*」で繋いだ交互作用を考慮したモデルになります。ここでは交互作用は考えません。
結果を見るには、summary関数を使います。
summary(result)
表示された以下のようになりました。
Df Sum Sq Mean Sq F value Pr(>F)
block 2 0.5543 0.2772 13.80 0.01603 *
treatment 2 0.7305 0.3652 18.18 0.00982 **
Residuals 4 0.0804 0.0201
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
3行目のtreatmentの行に注目をすると、P値(Pr(>F))が0.00982と有意水準1%よりも小さくなっています。これは、有意水準1%で考えたときに、N0・N10・N20の3つのグループで母平均が等しいという帰無仮説が棄却されることを示しています。つまり、施肥によってBrixに差がありそうだと言えるような結果です。
上記結果について詳しくはこちら
各列について、Dfは自由度、Sum Sqは平方和、Mean Sqは平均平方、F valueはF値、Pr(>F)はP値の結果を表示しています。各行について、blockはブロック、treatmentは処理、Residualsは誤差を示しています。検定はP値の値で判断しますが、平均平方やF値では効果の相対的な大きさなどを見ることができます。
アスタリスク*記号は、有意であることの記号で、***で0.1%有意、**で1%有意、*で5%有意であることを示しています。上記の結果では、ブロックの効果も5%有意になっているので、ブロックごとにもBrixに差があると考えられます。乱塊法を行うことでデータのバイアスを抑えることができました。
無事に一元配置分散分析を実行できました。
さて、aov関数の代わりにanova関数を用いても似たような検定を行うことができます。
その場合は、以下のように線形回帰モデルlm()に一度渡してから、それをanova関数に渡します。
model <- lm(brix ~ block + treatment, data = data)
result <- anova(model)
# 結果を見る
result
結果が以下のようになりました。
Analysis of Variance Table
Response: brix
Df Sum Sq Mean Sq F value Pr(>F)
block 2 0.55431 0.27716 13.796 0.016031 *
treatment 2 0.73047 0.36523 18.180 0.009822 **
Residuals 4 0.08036 0.02009
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
この場合も、P値(Pr(>F))が0.009822と、有意水準1%よりも小さい結果でした。
以上が一元配置分散分析になります。これでわかること処理間で差があるか/処理の効果がありそうかどうかであり、どの処理間で差があるのかを特定することまではできません。その場合は分散分析ではなく多重比較法という方法を用いて調べていくことになります。
3. スクリプト
以下はこれまでのコードをまとめたものです。
# データの生成(正規分布乱数)
set.seed(2021)
v <- matrix(c(
c(rnorm(3, 5.0, 0.25),rnorm(3, 4.8, 0.25), rnorm(3, 4.5, 0.25)),
c(rnorm(3, 4.6, 0.25),rnorm(3, 4.2, 0.25),rnorm(3, 4.2, 0.25)),
c(rnorm(3, 4.4, 0.25),rnorm(3, 4.1, 0.25),rnorm(3, 3.9, 0.25))
),nrow=9)
b <- factor(c(rep("1",3),rep("2",3),rep("3",3)))
raw_data <- data.frame(b,v)
colnames(raw_data) <- c("block","N0","N10","N20")
####################################
# データフレームの変形
# install.packages("tidyverse")
library(tidyverse)
df <- raw_data %>%
pivot_longer(col = -block, names_to = "treatment", values_to = "value")
####################################
# プロットごとに平均
data <- dataframe %>%
group_by(block,treatment) %>%
summarise(brix = mean(value))
####################################
# データの可視化
g <- ggplot(data, aes(x = treatment, y = brix))+
geom_boxplot()
g
####################################
# One-way ANOVA(aov()を用いる場合)
result <- aov(brix ~ block + treatment, data = data)
summary(result)
####################################
# One-way ANOVA(anova()を用いる場合)
model <- lm(brix ~ block + treatment, data = data)
result <- anova(model)
result