相関と回帰
今回は、Rを使った相関分析や線形回帰のやり方を紹介します。
相関とは、2つの変数の間の関係性を表現する言葉です。一方の変数が変化した時にもう一方の変数も変化するような関係を「相関がある」と言います。特に、一方が増えるともう一方も増えるような関係性を「正の相関」、一方が増えるともう一方は減るような関係性を「負の相関」と言います。いずれの関係も認められない時は「2つの変数に相関がない」ということになります。
この相関を数値で表したものを相関係数と言い、-1から1の間の値を取ります。正の相関がある場合は相関係数が1に近くなり、負の相関係数がある場合は-1に近くなり、相関がない場合は0に近くなります。
回帰とは、関数(モデル)を当てはめて、ある変数を別の変数で説明することを言います。説明される変数を目的変数(従属変数)、説明に用いられる変数を説明変数(独立変数)と言います。目的変数をY、説明変数をXとすると、回帰式 Y=f(X) で表現されます。
目的変数を説明変数の線形結合で説明することを線形回帰と言い、その最もシンプルなモデルは Y = aX + b となります。これは、目的変数を一つの説明変数で説明することから単回帰モデルと呼ばれます。このように、XとYのデータからパラメーターaやbを推定してモデルを構築することを回帰分析と言います。構築したモデルを用いて未知のデータYを算出することは予測と呼ばれます。
相関分析も上記の単回帰分析も二つの変数の関係性を分析する手法です。今回はこの相関と回帰の方法を具体的な圃場データを想定しながら紹介します。
解析(1)
データとしては、ホウレンソウの硝酸態窒素濃度(mg/100g)と生鮮重(g/plant) に関する、サンプル数n=36のデータを作って解析してみます。
データ
正規分布乱数nnorm()を使って仮想データを作ります。ここでは、Y = 0.05 × X + b という式で、Xとbに正規乱数を適用してXとYのデータを作っています。
set.seed(99)
x <- c(rnorm(36, 300, 100))
y <- x*0.05+10+rnorm(36,0,7)
df <- data.frame(NO3=x, weight=y)
以下のようなデータフレームになっています。
> head(df)
NO3 weight
1 321.3963 24.68746
2 347.9658 27.87489
3 308.7829 26.07267
4 344.3859 29.47861
5 263.7162 24.11666
6 312.2674 13.85852
散布図
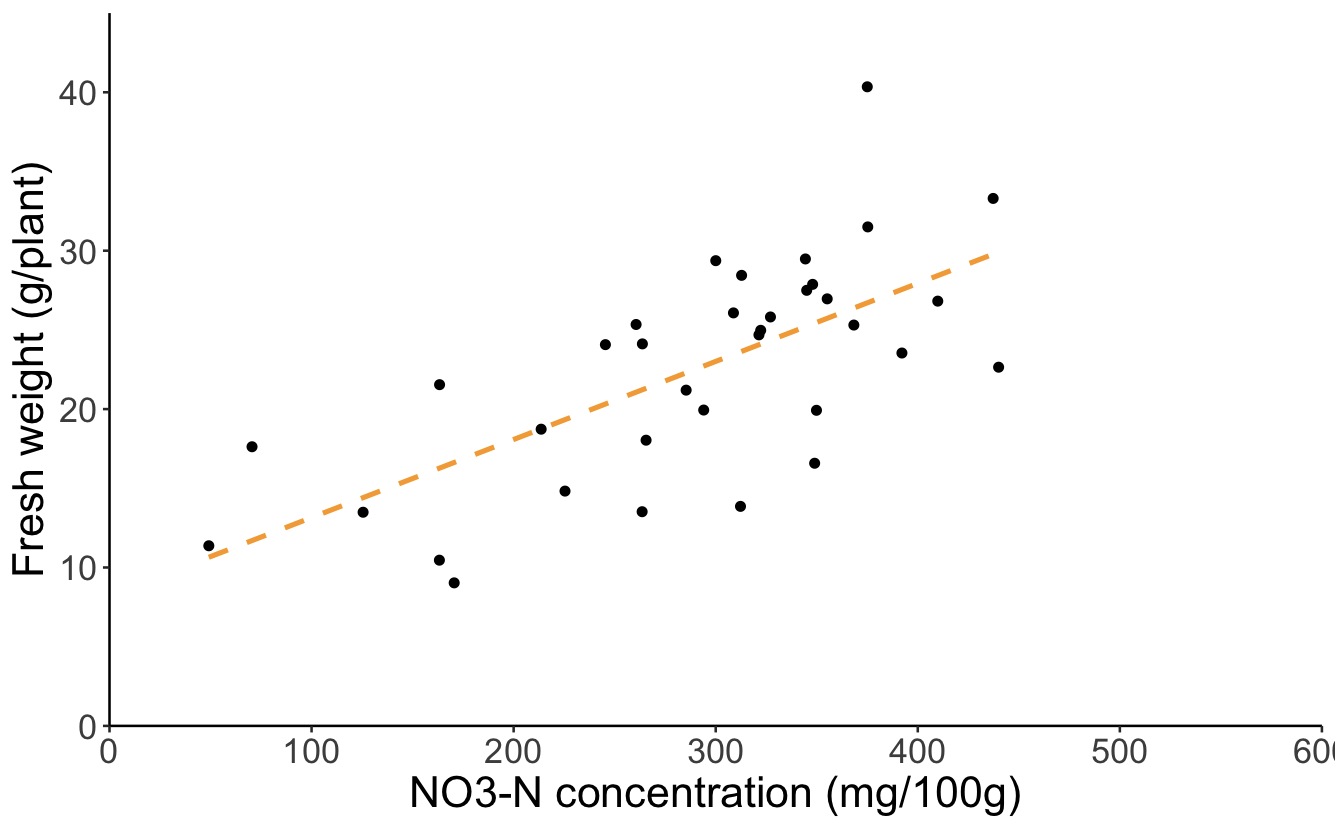
まずは、散布図を描写して、NO3とweightの関係を可視化します。plot()でも散布図がかけますが、ここではggplotを使いました。geom_smooth()を使って回帰直線も描いています。
library(ggplot2)
g <- ggplot(df, aes(x = NO3, y = weight))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, col="orange")+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
グラフにしてみることで、硝酸態窒素濃度と生鮮重の間に正の相関がありそうなことがわかります。
相関分析
次に相関係数を計算して、その相関が有意かどうかを検定してみます。これは関数cor.test()を使って1行で実行できます。
cor.test(df$NO3, df$weight)
結果は以下のようになりました。相関係数が0.7494747、p値が1.44e-07(1.44×10^(-7))と出ていて、有意に正に相関していることが言えます。
Pearson's product-moment correlation
data: df$NO3 and df$weight
t = 6.6011, df = 34, p-value = 1.443e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5584442 0.8650178
sample estimates:
cor
0.7494747
線形回帰
次に回帰も行ってみます。Rにデフォルトで入っている線形回帰の関数lm()を使ってモデルを作ります。回帰を行う時には、引数に「目的変数名 ~ 説明変数名, データ」の形でデータを渡すことが多いです。結果を一度model(文字列ならなんでもいいです)という変数に格納してから、summary()に渡して結果を見ます。
model <- lm(weight ~ NO3, data = df)
summary(model)
結果は以下の通りです。Coefficients:以下を見ると、(Intercept)(切片)とNO3の傾きの推定値 (Estimate)、標準誤差 (Std. Error)、t値 (t value)およびp値 (Pr) が表示されています。今回は、切片も傾きも有意でどちらも0ではないことがわかります。推定された回帰モデルは weight = 0.056017 × NO3 + 6.069252 で書けます。
Call:
lm(formula = weight ~ NO3, data = df)
Residuals:
Min 1Q Median 3Q Max
-9.7030 -4.0293 0.7737 3.4856 13.2709
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.069252 2.551804 2.378 0.0231 *
NO3 0.056017 0.008486 6.601 1.44e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.325 on 34 degrees of freedom
Multiple R-squared: 0.5617, Adjusted R-squared: 0.5488
F-statistic: 43.57 on 1 and 34 DF, p-value: 1.443e-07
解析(2)
次に、1月と7月と10月にそれぞれ12個ずつサンプルを取って36のサンプルを得た場合を想定してデータを作ってみます。月によって y切片に差があると仮定してそれぞれデータを作っています。
データ
set.seed(100)
x <- c(rnorm(12, 240, 50), rnorm(12, 300, 50), rnorm(12, 360, 50))
y <- c(x[ 1:12]*0.07+rnorm(12,10,5),
x[13:24]*0.07+rnorm(12,5,5),
x[25:36]*0.07+rnorm(12,-5,5))
t <- as.factor(c(rep("Jan.",12),rep("Oct.",12),rep("Jul.",12)))
df <- data.frame(NO3=x, weight=y, treatment=t)
以下のようなデータフレームになります。三列目にサンプリング月の文字列(Jan.,Jul.,oct.)を入れています。
> head(df)
NO3 weight treatment
1 214.8904 25.95687 Jan.
2 246.5766 29.34698 Jan.
3 236.0541 31.85080 Jan.
4 284.3392 34.75476 Jan.
5 245.8486 26.70125 Jan.
6 255.9315 34.93122 Jan.
散布図
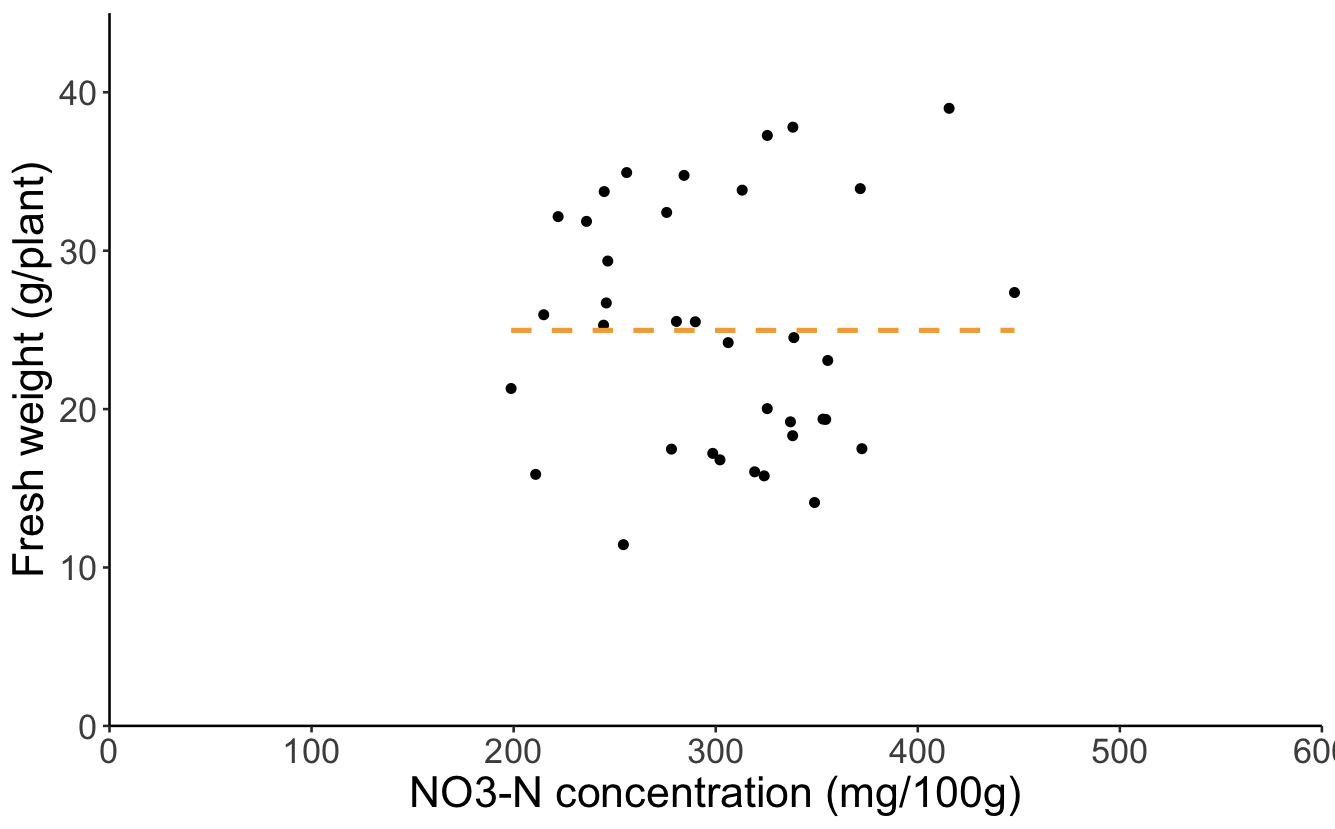
今回のデータでも同様に散布図を描いてみます。
g <- ggplot(df, aes(x = NO3, y = weight))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, col="orange")+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
すると以下のように、回帰直線が水平で、相関関係のなさそうなグラフができます。
相関分析
相関分析をしても、相関係数は0に近い値になります。
cor.test(df$NO3, df$weight)
Pearson's product-moment correlation
data: df$NO3 and df$weight
t = -0.00010902, df = 34, p-value = 0.9999
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.3285524 0.3285191
sample estimates:
cor
-1.869627e-05
線形回帰
回帰をしても同様で、NO3の回帰係数は0に近い値になります。
Call:
lm(formula = weight ~ NO3, data = df)
Residuals:
Min 1Q Median 3Q Max
-13.5279 -6.8539 -0.0648 7.2476 14.0188
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.497e+01 7.017e+00 3.559 0.00112 **
NO3 -2.489e-06 2.283e-02 0.000 0.99991
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 7.852 on 34 degrees of freedom
Multiple R-squared: 3.496e-10, Adjusted R-squared: -0.02941
F-statistic: 1.188e-08 on 1 and 34 DF, p-value: 0.9999
散布図(グループで色分け)
それでは、硝酸態窒素濃度と生鮮重に関係は見られなかったと結論づけてもいいのでしょうか?
実はサンプリングを3つの時期に分けてサンプリングしたことを考慮することが重要になってきます。つまり、母集団の違うデータを一緒にしてプロットすると、母集団の違いの効果が邪魔をして、背景にある共通の関係性が見えなくなってしまうことがあります。
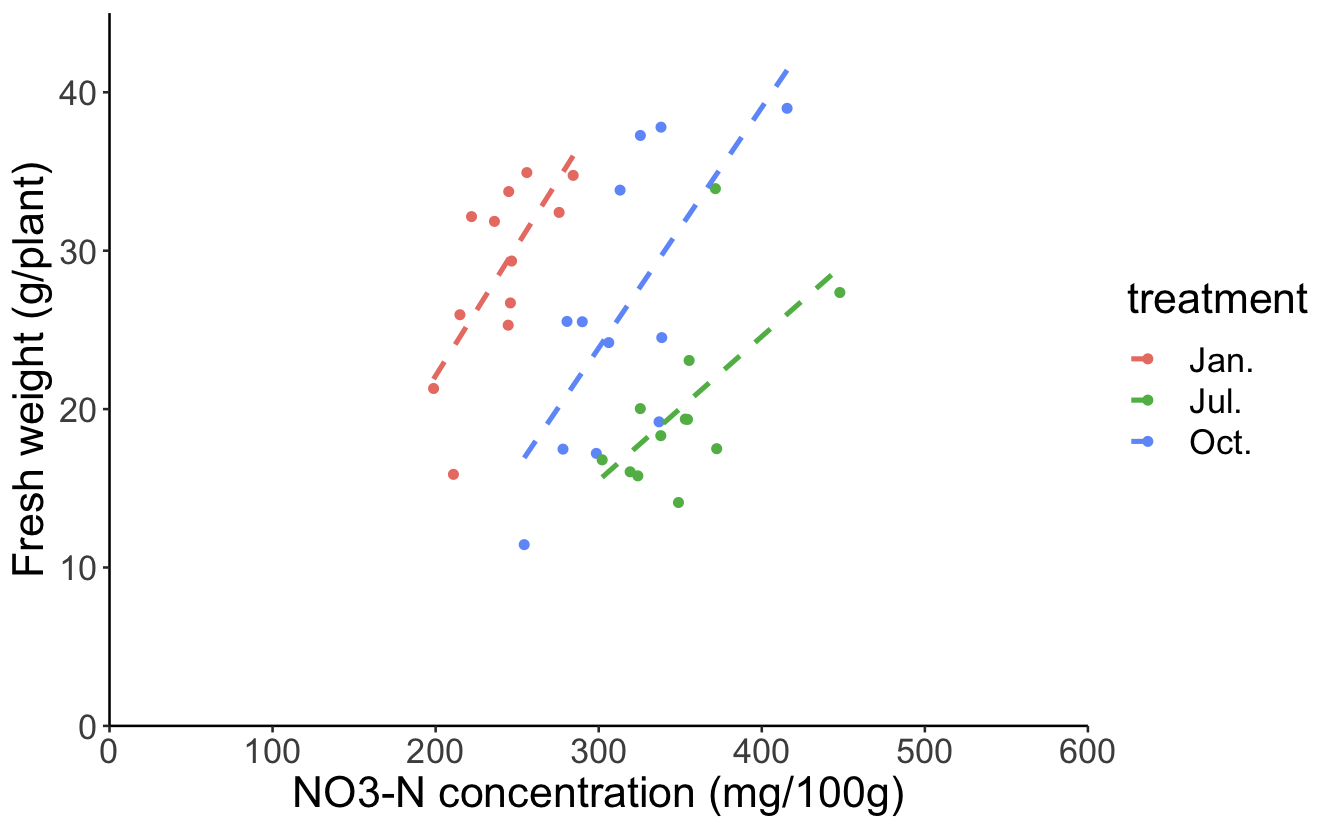
そこで、サンプリングの月で色分けをしてもう一度グラフを描いてみます。ggplotでcolor = treatment でtreatmentの要素に応じて色分けすることを指定しています。また、geom_point()に引数に mapping = aes(colour = treatment) を入れることで、グループごとに回帰直線を描いてみます。
g <- ggplot(df, aes(x = NO3, y = weight, color = treatment))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, mapping = aes(colour = treatment))+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
すると、以下のグラフのようにそれぞれの月毎に見ると、NO3とweightの間に正の相関があるようなグラフを描くことができます。
線形混合(効果)モデル回帰
サンプリング月の情報を回帰に反映させるために使えるのが、線形混合モデルまたは線形混合効果モデル(Linear mixed (mixed-effect) model)と呼ばれるモデルです。このモデルでは、硝酸態窒素が与える効果を固定効果、サンプル月が与える効果をランダム効果として扱います。すると、サンプリングを行った月によって、モデルの切片や傾きが異なるようなモデルを考え考えることができます。
線形混合モデルを使うには、lme4パッケージやlmerTestパッケージが使えます。関数lmer()で回帰モデルを構築しますが、その際に (NO3 | treatment) という項を加えることで、モデルのy切片とNO3の係数がtreatmentのランダム効果を受けることを想定することができます。係数は固定で切片のみランダム効果の影響を受けると想定するときは、(1 | treatment)に、切片は固定で係数のみランダム効果を受けると想定するときは(0 + NO3 | treatment)とします。今回は、データを作るときに傾きは固定で切片を変えたので(1 | treatment)にしました。
# install.packages("lmerTest")
library(lmerTest)
model2 <- lmerTest::lmer(weight ~ NO3 + (1 | treatment), data=df)
summary(model2)
結果は以下の通りです。Random effects:以下ではランダム効果の結果が、Fixed effects:以下では固定効果の結果が見られます。これをみると、NO3の固定効果が有意に検出され (p値=3.04e-05)、係数が0.1248と推定されています。つまり、切片がサンプル月によるランダムな効果を受けると過程をすると、硝酸態窒素と生鮮重の正の相関関係が見えてきたということになりました。
Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
Formula: weight ~ NO3 + (1 | treatment)
Data: df
REML criterion at convergence: 232.9
Scaled residuals:
Min 1Q Median 3Q Max
-1.80623 -0.71236 -0.06904 0.57474 2.05570
Random effects:
Groups Name Variance Std.Dev.
treatment (Intercept) 125.46 11.20
Residual 28.73 5.36
Number of obs: 36, groups: treatment, 3
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) -12.6966 10.1866 9.2168 -1.246 0.243
NO3 0.1248 0.0259 33.6182 4.817 3.04e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr)
NO3 -0.768
以上が、相関分析・線形回帰・線形混合モデル回帰でした。線形混合モデルは分野によってはあまり使われないのかもしれませんが、複数の条件の異なる地点やタイミングでサンプリングを行ったデータの解析に使えるかもしれないモデルだと思うので、紹介しました。
コード
et.seed(99)
x <- c(rnorm(36, 300, 100))
y <- x*0.05+10+rnorm(36,0,7)
df <- data.frame(NO3=x, weight=y)
g <- ggplot(df, aes(x = NO3, y = weight))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, col="orange")+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
cor.test(df$NO3, df$weight)
model <- lm(weight ~ NO3, data = df)
summary(model)
set.seed(100)
x <- c(rnorm(12, 240, 50), rnorm(12, 300, 50), rnorm(12, 360, 50))
y <- c(x[ 1:12]*0.07+rnorm(12,10,5),
x[13:24]*0.07+rnorm(12,5,5),
x[25:36]*0.07+rnorm(12,-5,5))
t <- as.factor(c(rep("Jan.",12),rep("Oct.",12),rep("Jul.",12)))
df <- data.frame(NO3=x, weight=y, treatment=t)
g <- ggplot(df, aes(x = NO3, y = weight))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, col="orange")+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
cor.test(df$NO3, df$weight)
model1 <- lm(weight ~ NO3, data = df)
summary(model1)
g <- ggplot(df, aes(x = NO3, y = weight, color = treatment))+
geom_point()+
geom_smooth(method = "lm", linetype = "dashed", se = FALSE, mapping = aes(colour = treatment))+
scale_y_continuous(expand = c(0,0),limits = c(0,45))+
scale_x_continuous(expand = c(0,0),limits = c(0,600))+
labs(x = "NO3-N concentration (mg/100g)", y = "Fresh weight (g/plant)")+
theme_classic()+
theme(text = element_text(size=18))
g
library(lmerTest)
model2 <- lmer(weight ~ NO3 + (1 | treatment), data=df)
summary(model2)