ヤッツィーとは
ヤッツィーはサイコロを複数回振り、出た目に合わせて役を選択することを繰り返し、合計点を競うというボードゲームです。運が絡む要素が多いので実力があまり関係しないゲームだと思われがちですが、麻雀と同じように何度も繰り返すと強い人が勝ち越します。
このような確率的に進行するボードゲームの期待値を求めることなんてできるのか?答えはYesです、競技プログラミングで培った知識を使えば解けます。もしあなたが競技プログラミングをやっている人のことを「競プロ界隈でしか使えない狭い知識を習得して喜んでいるITもどき」だと思っているのであれば、その考えを覆さざるを得ない反例をご覧に入れましょう。
解析方法
大まかな方針
最初からいっぺんに問題を解く方法を探すのは困難です。まずは問題を細分化してみましょう。
このゲームでプレイヤーが選択を行えるのは以下の場面です。
- サイコロを振ったあと、5つのうちどのサイコロを振り直すか選択(2回まで)
- 1の手順によってサイコロの出目が決定したあと、どの役に登録するか選択
この2つの場面において、期待値を最大化するような選択を行えるようにしたいです。
サイコロの出目が決定したあと、どの役に登録するか選択
まずはサイコロを振り直せるというルールを無視して、サイコロの出目が決まったときにどの役に登録するのが最善かについて考えてみます。
いきなり12個の役から考えるのは大変なので、一番最後の1個しか選べない状況から考えていきます。これは競プロでぼちぼち使う後退解析という手法に基づくものです。
①選べる役が1個の場合
具体例で考えてみます。例えば選べる役がフルハウスのみだった場合、サイコロの出目に関わらずフルハウスに登録するのが最善となり、出目がフルハウスであれば出目の合計、そうでなければ$0$点が得点となります。
これをすべての出目のパターンについて、(その出目になる確率)×(得点)を求めて合計を出せば、その値が「残りの役がフルハウスのみの場合の期待値」になります。
このように、選べる役が一つの場合の期待値は簡単に求まります。
②選べる役が2個の場合
この場合は①の結果を利用します。具体例として、選べる役がフルハウス、Bストレートの2つで、且つサイコロの出目が$(1, 2, 3, 4, 5)$だった場合について考えます。
- フルハウスを選んだ場合、この時の得点は$0$点となり、①で求めたBストレートのみの期待値がそのままこの場合の期待値となります。
- Bストレートを選んだ場合、この時の得点は$30$点となり、①で求めたフルハウスのみの期待値と合わせた値がこの場合の期待値となります。
このようにしてそれぞれの役を選んだ場合の期待値を求めることができ、1, 2のうち期待値が高い方が最善な選択であり、出目の期待値となります。あとは①のときと同様に、すべての出目のパターンについて(その出目になる確率)×(期待値が高い方の得点)を求めて合計を出していくことで、選べる役が2つの場合の期待値を求めることができます。
③選べる役がn個の場合
一般化した場合を考えます。今選べる役の集合を$S$とし、この時の期待値$E[S]$を求めます。ここでサイコロの出目が出目$i$となり、役$j$を選択したとき得られるポイントを$P_{ij}$とします。すると遷移先は$S$から$j$を除いた差集合となるため、$E[S]$は以下のように求められます。
$$ E[S] = max(P_{ij} + E[S \setminus j]) (j \in S)$$
以上の式を$S$の要素数が少ない順に求めていけば、全ての役が含まれている場合=ゲーム開始時の初期値を求める事ができます。
このように小さな問題の結果を利用して大きな問題の結果を求めていく手法を動的計画法と呼び、競プロ界だと登竜門的な扱いとなっています。今回のような漸化式の添字が集合となる場合は集合を2進法で表すことができ、このような動的計画法を特にbitDPと呼んだりします。
2. サイコロを振ったあと、5つのうちどのサイコロを振り直すか選択(2回まで)
1の方法で、出目が確定した時にどの役に登録すべきか求めることができます。
しかしヤッツィーでは良い出目だけ保存し、2回までサイコロを振り直せるという解析上厄介なルールがあります。このルールも上手く対処したいです。
まず振り直しのパターンについて考えます。サイコロは5つあり、それぞれについて振り直すか振り直さないかに分類すると、場合の数は$2^5=32$通りあります。この組み合わせ全てについて期待値を求め、最も期待値が大きい選択を採用したいです。
ある出目から特定のサイコロを振り直した時の遷移について考えます。具体例として、出目が(1,1,2,3,5)からサイコロを1回だけ振り直すことを考えます。あと$n$回振り直し可能な出目$x$の期待値を$E_n[x]$として表します。
-
(1,1,2,3,5)全てを残す場合の遷移
この場合は当然、遷移先は(1,1,2,3,5)しかありません。
よって期待値は以下のようになります。
$$ E_1[(1,1,2,3,5)] = E_0[(1,1,2,3,5)] \times 1 $$ -
(1,1,2,3)を残して(5)だけ振り直す場合の遷移
この場合の遷移先は1つのサイコロの出目によって6つあります。
よって期待値は以下のようになります。
$$ E_0[(1,1,2,3)] = (E_1[(1,1,1,2,3)] + E_1[(1,1,2,2,3)] + E_1[(1,1,2,3,3)] + E_1[(1,1,2,3,4)] + E_1[(1,1,2,3,5)] + E_1[(1,1,2,3,6]) \times \frac{1}{6} $$
これと同じように全ての遷移について求め、出目ごとに期待値が最大となる遷移の期待値を記録します。これを全ての出目について行えば、振り直し1回前の期待値について求めることができます。よってこの操作を2回繰り返すことで始めの状態の期待値を求めることができます。
3. ボーナスを考慮
このゲームで2番目に解析上厄介なルールとして、エース, デュース, ... , シックス($n$の目の数×$n$が得点)という役で取った得点の合計が$63$点を超えると、追加ボーナスとして$35$点がもらえるという仕様があります。
これは、1で作成した動的計画法テーブルに、今までエース, デュース, ... , シックスの役で取った点数の記録を追加し、(集合$S$)と($n$の目合計得点)の2つの状態を持った二次元テーブルを用意することで対処します。
結果
1. 期待値と分布
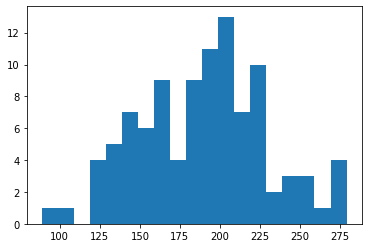
解析の結果、期待値は$191.76$点であることがわかりました。このゲームは普通にやると$170$点前後で終わることが多く、$200$点を超えるとめちゃくちゃラッキーというのが体感なので、平均で$190$点以上が出せるのであれば結構強いと思います。(個人的な感想)
最小値は$89$点、最大値は$276$点、平均値は$189.4$点となりました。
ヒストグラムでは$200$点あたりが最頻値となっており、平均値もおよそ理論値に従っています。
ただしこの最適手順には問題もあって、対戦相手の点数を全く考慮していません。なので安全策をとることよりも、確率は低くても期待値は高い手順を優先します。
平均して高い得点を取る上では最適手順ですが、対戦で勝つためには必ずしも最適手順でない点に注意してください。
2. 実際の進行例
長いですが、進行例の出力をまとめました。
()内は5つのサイコロの出目を表し、その下に第3候補までの選択を示しています。そして自動的に第1候補の手順を選択します。
-
選択:(6, 6)の場合は該当するサイコロの出目のみを保存し、残りのサイコロを振り直すことを意味します。振り直したサイコロはランダムに値が決定し、次の出目となります。 -
選択:シックス(6)の場合は確定したサイコロの出目を役シックスに登録することを意味します。そして役状況から役シックスが除外されます。
以下ログです。要所で補足説明を追加しました。
○進行状況 → 1/12
(1, 1, 4, 6, 6)
第1候補 期待値:191.78712657351343, 選択:(6, 6)
第2候補 期待値:190.12939146059352, 選択:(4, 6, 6)
第3候補 期待値:189.67736745290577, 選択:(1, 6, 6)
(2, 2, 5, 6, 6)
第1候補 期待値:186.37335697040936, 選択:(6, 6)
第2候補 期待値:185.5800234369072, 選択:(5, 6, 6)
第3候補 期待値:184.75582563604303, 選択:(2, 2)
(2, 4, 6, 6, 6)
第1候補 期待値:188.5846526307905, 選択:シックス(6)
第2候補 期待値:182.63876414601035, 選択:チョイス
第3候補 期待値:176.29234285786612, 選択:エース(1)
現在の得点:18, ボーナスまで:45, 役状況:000000100000
6の目が多くなるように振り直し、役シックスに登録したことが読み取れます。
○進行状況 → 2/12
(1, 2, 2, 6, 6)
第1候補 期待値:186.23284005224738, 選択:(6, 6)
第2候補 期待値:185.4773953551066, 選択:(2, 2)
第3候補 期待値:184.39936242767487, 選択:()
(1, 5, 6, 6, 6)
第1候補 期待値:187.78811855441796, 選択:(6, 6, 6)
第2候補 期待値:186.83168344037145, 選択:(5, 6, 6, 6)
第3候補 期待値:182.83168344037145, 選択:(1, 6, 6, 6)
(2, 5, 6, 6, 6)
第1候補 期待値:180.35573093266132, 選択:チョイス
第2候補 期待値:172.6677534184262, 選択:ヨット
第3候補 期待値:172.31934794186498, 選択:エース(1)
現在の得点:43, ボーナスまで:45, 役状況:000001100000
チョイスとは出目のパターンに関わらず、目の合計をそのまま得点に加算する役です。
○進行状況 → 3/12
(1, 2, 2, 5, 5)
第1候補 期待値:179.92173012290758, 選択:(5, 5)
第2候補 期待値:177.94458061674766, 選択:(2, 5, 5)
第3候補 期待値:177.62114988680335, 選択:(1, 5, 5)
(1, 2, 2, 5, 5)
第1候補 期待値:174.06101600176413, 選択:(5, 5)
第2候補 期待値:173.63596641881077, 選択:(2, 2)
第3候補 期待値:172.78853351721065, 選択:(2, 2, 5, 5)
(2, 3, 5, 5, 5)
第1候補 期待値:176.99872446094872, 選択:ファイブ(5)
第2候補 期待値:165.05999241579946, 選択:ヨット
第3候補 期待値:164.82556659378702, 選択:エース(1)
現在の得点:58, ボーナスまで:30, 役状況:000001110000
○進行状況 → 4/12
(1, 2, 3, 5, 6)
第1候補 期待値:173.22930353208216, 選択:(3,)
第2候補 期待値:173.06793472623164, 選択:(2, 3)
第3候補 期待値:173.0189006610048, 選択:(2, 3, 5)
(2, 3, 3, 5, 6)
第1候補 期待値:170.28376578621015, 選択:(3, 3)
第2候補 期待値:168.42035411366595, 選択:(2, 3, 3)
第3候補 期待値:168.40328077141183, 選択:(3, 3, 5)
(1, 3, 3, 3, 6)
第1候補 期待値:174.17310942364014, 選択:トレイ(3)
第2候補 期待値:163.6881530341687, 選択:エース(1)
第3候補 期待値:162.10420480582815, 選択:ヨット
現在の得点:67, ボーナスまで:21, 役状況:000001110100
○進行状況 → 5/12
(1, 2, 4, 5, 6)
第1候補 期待値:171.058808487071, 選択:(4,)
第2候補 期待値:170.87055040511763, 選択:(2, 4)
第3候補 期待値:170.62779319943388, 選択:(2, 4, 5)
(3, 4, 4, 4, 6)
第1候補 期待値:179.8259221588793, 選択:(4, 4, 4)
第2候補 期待値:177.23564629796027, 選択:(4, 4, 4, 6)
第3候補 期待値:176.23564629796027, 選択:(3, 4, 4, 4)
(3, 4, 4, 4, 4)
第1候補 期待値:194.3039596914263, 選択:フォー(4)
第2候補 期待値:176.7434866028678, 選択:フォーダイス
第3候補 期待値:159.58794335335955, 選択:ヨット
現在の得点:83, ボーナスまで:5, 役状況:000001111100
○進行状況 → 6/12
(1, 1, 3, 4, 6)
第1候補 期待値:191.40673491869165, 選択:(3, 4)
第2候補 期待値:191.12458331586015, 選択:(4,)
第3候補 期待値:190.9766264087002, 選択:()
(1, 3, 4, 4, 5)
第1候補 期待値:189.26289311149407, 選択:(1, 3, 4, 5)
第2候補 期待値:188.5424340906984, 選択:(3, 4, 5)
第3候補 期待値:188.11211056532463, 選択:(1, 3, 4)
(1, 1, 3, 4, 5)
第1候補 期待値:186.17006312146418, 選択:エース(1)
第2候補 期待値:181.27097596032044, 選択:ヨット
第3候補 期待値:178.2335313172997, 選択:フォーダイス
現在の得点:85, ボーナスまで:3, 役状況:000001111101
エースは(得点)=(1の目の数×$1$点)の役で、最大でも$5$点しか入らないため、出目が良くなかったときにゴミ箱的に使われることが多い役です。
○進行状況 → 7/12
(1, 1, 2, 5, 5)
第1候補 期待値:183.68332388254453, 選択:(5, 5)
第2候補 期待値:183.4616173266695, 選択:(2,)
第3候補 期待値:183.31767903148574, 選択:(2, 5)
(3, 4, 5, 5, 6)
第1候補 期待値:184.48727322580436, 選択:(3, 4, 5, 6)
第2候補 期待値:182.01947634621166, 選択:(3, 4, 5, 5, 6)
第3候補 期待値:179.78560474942418, 選択:(3, 4, 5)
(2, 3, 4, 5, 6)
第1候補 期待値:196.82625762376784, 選択:B.ストレート
第2候補 期待値:182.01947634621166, 選択:S.ストレート
第3候補 期待値:173.29156993405076, 選択:ヨット
現在の得点:115, ボーナスまで:3, 役状況:010001111101
B.ストレートは5つの出目が全て連続している場合に$30$点もらえる役です。意外と揃えやすいです。
○進行状況 → 8/12
(1, 2, 3, 4, 5)
第1候補 期待値:195.90111851999592, 選択:(2, 3, 4, 5)
第2候補 期待値:195.90111851999592, 選択:(1, 2, 3, 4, 5)
第3候補 期待値:195.90111851999592, 選択:(1, 2, 3, 4)
(2, 3, 4, 5, 6)
第1候補 期待値:195.90111851999592, 選択:(3, 4, 5, 6)
第2候補 期待値:195.90111851999592, 選択:(2, 3, 4, 5, 6)
第3候補 期待値:195.90111851999592, 選択:(2, 3, 4, 5)
(3, 4, 4, 5, 6)
第1候補 期待値:195.90111851999592, 選択:S.ストレート
第2候補 期待値:185.13805402725234, 選択:ヨット
第3候補 期待値:182.4584281196837, 選択:フォーダイス
現在の得点:130, ボーナスまで:3, 役状況:011001111101
S.ストレートは4つの出目が全て連続している場合に$15$点もらえる役です。
○進行状況 → 9/12
(2, 4, 4, 5, 6)
第1候補 期待値:193.5438637480063, 選択:(2,)
第2候補 期待値:193.32447035010043, 選択:(4, 4)
第3候補 期待値:193.23288931675987, 選択:(2, 6)
(2, 3, 5, 5, 6)
第1候補 期待値:189.9981402608579, 選択:(2,)
第2候補 期待値:189.10287736990048, 選択:(2, 6)
第3候補 期待値:189.01491440693752, 選択:(2, 5)
(1, 2, 3, 4, 6)
第1候補 期待値:184.8404783653799, 選択:ヨット
第2候補 期待値:182.25941213570945, 選択:フォーダイス
第3候補 期待値:181.25314937139473, 選択:フルハウス
現在の得点:130, ボーナスまで:3, 役状況:111001111101
ヨットは5つの出目全てが同じ数字だったときに$50$点もらえる特大役です。ですが揃えられる確率は低いです、今回はゴミ箱役として使われました。
○進行状況 → 10/12
(1, 2, 2, 4, 4)
第1候補 期待値:187.18697927352054, 選択:(2, 2)
第2候補 期待値:186.835587688177, 選択:(2, 2, 4)
第3候補 期待値:186.79790089789998, 選択:(1, 2, 2)
(2, 2, 2, 3, 6)
第1候補 期待値:187.85223813351246, 選択:(2, 2, 2)
第2候補 期待値:187.84931407618228, 選択:(2, 2, 2, 6)
第3候補 期待値:187.43703349551095, 選択:(2, 2, 2, 3)
(1, 1, 2, 2, 2)
第1候補 期待値:187.10370016217757, 選択:デュース(2)
第2候補 期待値:179.57738364620567, 選択:フルハウス
第3候補 期待値:172.56089737908567, 選択:フォーダイス
現在の得点:171, ボーナスまで:0, 役状況:111001111111
ここでエース、デュース、... 、シックスの役の合計が$63$点を超えたので、ボーナスが加算されました。$130$点 → $171$点と大幅に得点に寄与しています。
○進行状況 → 11/12
(1, 2, 4, 4, 4)
第1候補 期待値:191.23173756680288, 選択:(4, 4, 4)
第2候補 期待値:189.2349397796067, 選択:(2, 4, 4, 4)
第3候補 期待値:188.90160644627338, 選択:(1, 4, 4, 4)
(4, 4, 4, 4, 5)
第1候補 期待値:198.96572650278372, 選択:(4, 4, 4, 4, 5)
第2候補 期待値:197.46572650278372, 選択:(4, 4, 4, 4)
第3候補 期待値:186.33316218679605, 選択:(4, 4, 4)
(4, 4, 4, 4, 5)
第1候補 期待値:198.96572650278372, 選択:フォーダイス
第2候補 期待値:176.61126342767236, 選択:フルハウス
現在の得点:192, ボーナスまで:0, 役状況:111011111111
フォーダイスは4つの出目が同じ数字だったときに出目の合計が得点となる役です。ここで得点の理論期待値を超えました。
○進行状況 → 12/12
(1, 2, 2, 3, 6)
第1候補 期待値:196.86574074074073, 選択:(2, 2, 6)
第2候補 期待値:196.2014317558299, 選択:(6,)
第3候補 期待値:195.98083847736626, 選択:(2, 2)
(2, 2, 2, 4, 6)
第1候補 期待値:195.0, 選択:(2, 2, 2, 6)
第2候補 期待値:194.33333333333334, 選択:(2, 2, 2, 4)
第3候補 期待値:193.88888888888889, 選択:(2, 2, 2)
(2, 2, 2, 5, 6)
第1候補 期待値:192.0, 選択:フルハウス
現在の得点:192, ボーナスまで:0, 役状況:111111111111
フルハウスは3つの同じ目と2つの同じ目を揃えると出目の合計が得点となる役です。今回は成立しませんでした。
以上です。既に役が揃ってる状況でも得点を少しでもあげようと必死に頑張ってるところがかわいいです。最適手順だから当たり前だけどめちゃくちゃ賢い。
まとめ
競技プログラミングの可能性は無限大