【ABC】 AtCorder 395 C - Shortest Duplicate Subarray

目的

AtCoder 395 C - Shortest Duplicate Subarrayの解法の考え方などを備忘録として残す。

問題

問題文

正整数N と、長さN の整数列A=(A1,A2,…,AN) が与えられます。
A の空でない連続部分列であって、同じ値を複数個含むようなものが存在するか判定してください。存在するならばそのようなもののうち最も短いものの長さを求めてください。

制約

• 1≤N≤2×10^5
• 1≤Ai≤10^6(1≤i≤N)
• 入力はすべて整数

目次

• 解法1-尺取法-
  • 尺取法とは
  • ソースコード
• 解法2-同じ数字の距離を計測-
  • 考え方
  • ソースコード

解法1-尺取法-

尺取法を用いた解法について解説する。

尺取法とは

1. 左を固定し条件に合致するまで右に走査を進める
2. 見つかったら左を一つ右にずらし、走査済みの次の要素から走査を進める
3. 1,2を範囲まで繰り返す

尺取法の計算量はO(n)となる。ソースコードだとfor-whileを使用し実装する。for二重ループ O(n^2)と比較すると計算量はかなり節約できる。
詳細は以下のページがわかりやすい。

ソースコード

#include <iostream>
#include <vector>

using namespace std;
#define rep(i, n) for (int i = 0; i < (int)n; ++i)
const int INF = 1 << 30;

/**
 * @brief 尺取り法を用いた解法
 * @return int 
 */
int main()
{
    int n;
    cin >> n;
    vector<int> a(n);
    rep(i,n) cin >> a[i];

    // 各数字の出現回数を記録するバケツを用意
    vector<int> cnt(1000005);
    // 複数個あるかどうか判別
    bool isMult = false;

    // l:左端, r:右端
    int ans = INF;
    int r = 0;
    // 尺取法 for-while
    rep(l,n) {
        // 右端まで行ってない && 2回目出てない
        while (r < n && isMult == false) {
            cnt[a[r]]++;
            if (cnt[a[r]] == 2) isMult = true;
            r++;
        }
        
        if (!isMult) break;        
        ans = min(ans, r-l);
        if (cnt[a[l]] == 2) isMult = false;
        cnt[a[l]]--;
    }

    if (ans == INF) ans = -1;
    cout << ans << endl;
    
    return 0;
}

解法2-同じ数字の距離を計測-

考え方

1. 各数字とその出現場所を覚えておく
2. 同じ数字2回以上出現していたら、その距離を計算する
3. 2を最後まで繰り返す

以下の6つの数字の入力を例に解説する。

1. 各数字とその出現場所を覚えておく

   数字	出現場所
   1	1, 4, 6
   2	2, 5
   3	3

2. 同じ数字2回以上出現していたら、その距離を計算する
   1は3回出てきており、それぞれの距離を計算すると最短が3となる。

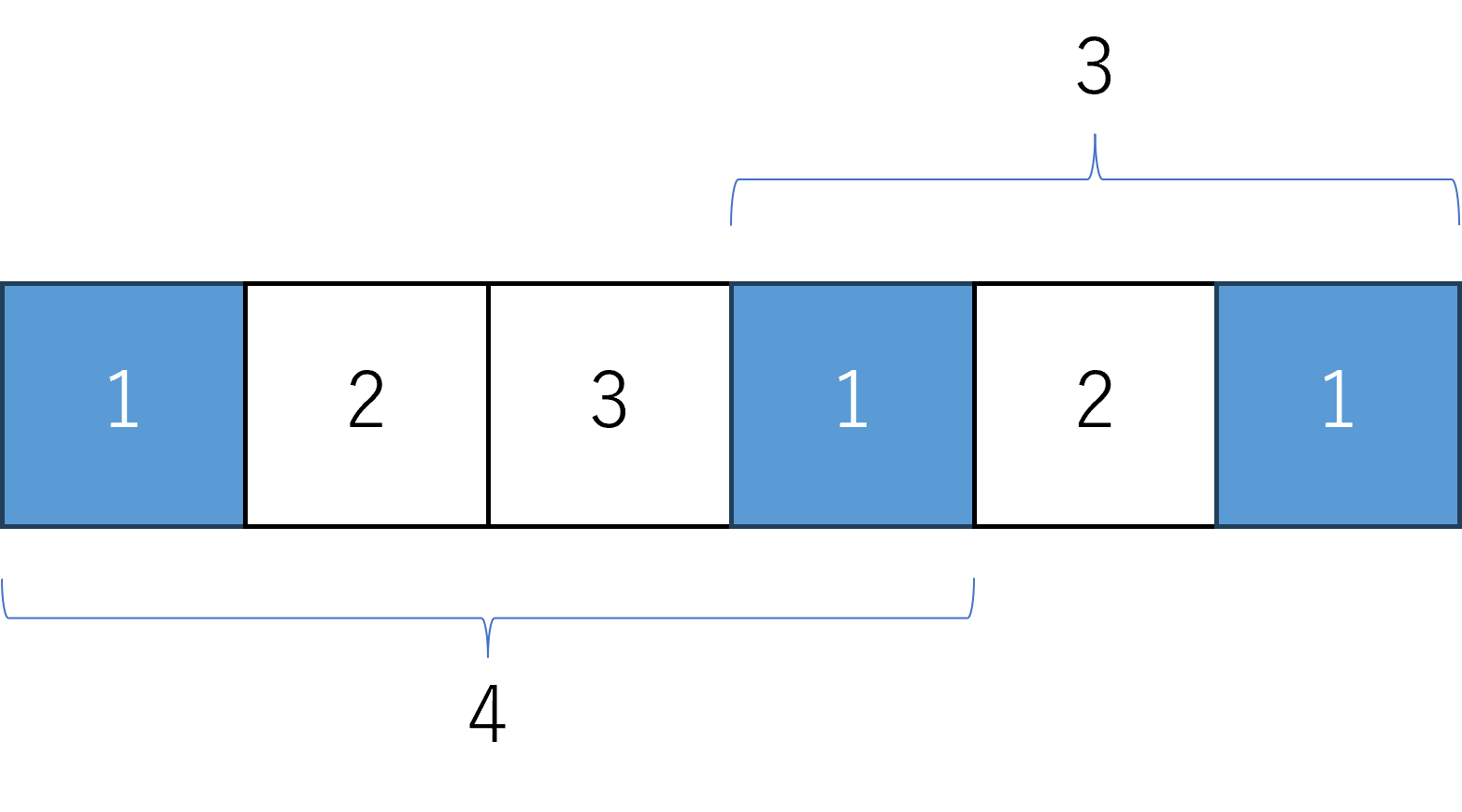
1. 2を最後まで繰り返す
   同様に数字2,3に対しても行う。ただし、3は1回しか出現していないため、距離はない。

最終的な回答は3となる。

ソースコード

#include <iostream>
#include <vector>
#include <map>

using namespace std;
#define rep(i, n) for (int i = 0; i < (int)n; ++i)
constexpr int INF = 1 << 30;

/**
 * @brief 2回以上出現した数字のキョリを測る解法
 * @return int 
 */
int main()
{
    // 入力
    int n;
    cin >> n;
    vector<int> a(n);
    rep(i,n) cin >> a[i];

    // Key:出現数字、Value:出現場所
    map<int, vector<int>> intMap;
    rep(i,n) {
        // 数字がMapになければ追加、Mapにあれば出現場所をValueに追加
        if (intMap.end() == intMap.find(a[i])) intMap.insert(pair(a[i], vector<int>{i}));
        else intMap[a[i]].push_back(i);
    }

    // 同じ数字が出現した距離を計算
    int ans = INF;
    for (auto v: intMap) {
        rep(i,v.second.size()-1) ans = min(ans, v.second[i+1]-v.second[i]+1);
    }

    // 出力
    if (ans == INF) ans = -1;
    cout << ans << endl;
    
    return 0;
    }