初めに
こちらのタイトルは,もう察していらっしゃる方はいるかもしれませんが,こちらの本を参考にしました.(内容は恥ずかしながら読めていませんが,因子分析とはなんぞやという入門的な内容としてよくおすすめされている印象があります)
誰も教えてくれなかった因子分析 数式が絶対に出てこない因子分析入門

因子分析は,人文系の学生ならほとんど教養の授業の中で習うと思うので聞いたことがある人は多いのではないでしょうか.しかし,実際に「因子分析ってなんだっけ?」ってなって調べると,「SPSSで因子分析しましょ」みたいな知見 or How toベースな記事がほとんどだと思います.ここをこうぽちぽちして...この数値はこういう意味を持っていて...なんかバリマックス法よりプロマックス法の方がいいらしい...まずimport sklearnしてもらって...みたいな内容のものがほとんどだと思います(偏見かもしれないです).確かに経験的な理解は大事です.個人的には理論ばかり追っていて頭でっかちの重箱のすみ突きマンになっては元も子もないと思っています.しかし,だからと言って因子分析の理論部分をおざなりにしてはいけないと思います.そこで自分が因子分析を勉強した内容をもとに本記事を作成しようと思いました.より詳細な内容は最後の方にお勧めする書籍で各自勉強していただければと思います.もし僕のこの記事を参考に理論部分に興味を持つ方が現れたり,実装から理論への架け橋に慣れたりしたら幸いです...
対象とする方
- 因子分析の概要は知っているが,何をやって出てきたものなのかわからないし,計算手順が気になる
- 学部生程度の数理統計の知識がある
- 因子分析の本を読むほどモチベーション or 時間はないが,なんとなく把握したい
本記事の注意
そこで本記事では因子分析の理論的な背景を自分の勉強/ゼミ用に使用した資料をもとに制作されています.ただあくまで僕は数理統計の専門的な教育を受けたわけではないので,間違っている可能性があります.もし間違いを見つけた方がいられましたら,コメントの方にご一報くださればと思います.
記事の構成
これから更新予定の記事は下記のようになる予定です.今回の記事は概要編になります.こちらで変数名の定義等々を行っていきたいと思います.
- ある意味誰も教えてくれなかった因子分析(概要&定義編) ← こちら
- ある意味誰も教えてくれなかった因子分析(初期解推定編)
- ある意味誰も教えてくれなかった因子分析(因子回転編)
- ある意味誰も教えてくれなかった因子分析(因子選択編)
- ある意味誰も教えてくれなかった因子分析(因子得点推定編)
言葉の定義
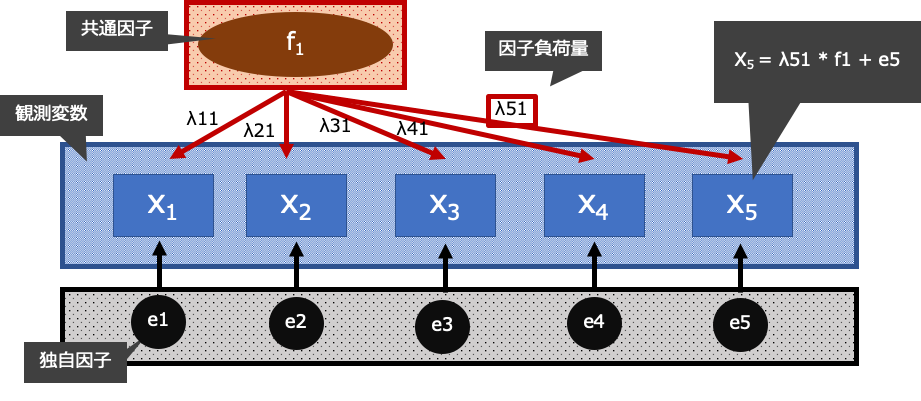
因子分析は,観測変数のみが得られた状態で.その背景にあるはずの潜在因子である共通因子と独自因子に分解する場合の各要素を推定する方法です.
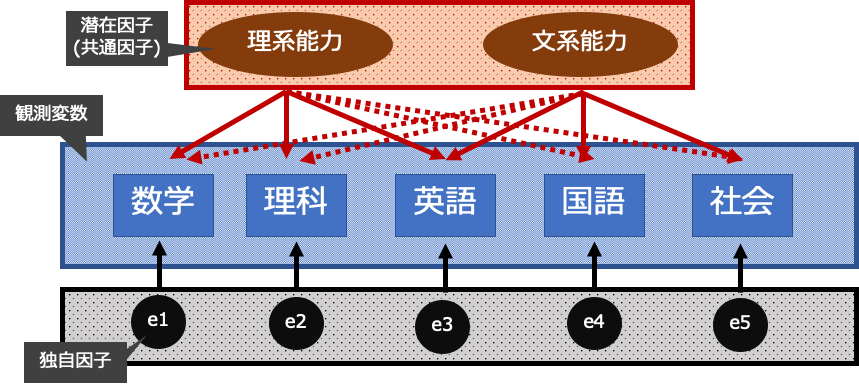
例えば,それぞれの変数を下記のような図に表すと,$ x_5 $ という変数は, $ x_5 = \lambda_{51} * f_1 + e_5 $ という形で表すことができるような因子負荷量 $ \lambda $, 独自因子(の分散) $ e $,必要であれば因子得点 $ f $を推定する手法になります.
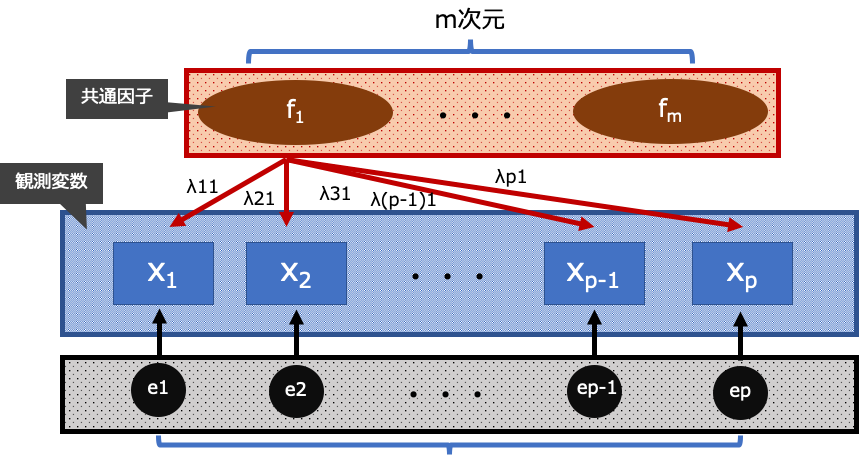
より一般的な表記にすると下記のような図になります.潜在因子がm次元で,p次元の観測変数をうまい具合に説明したい問題を考えます.
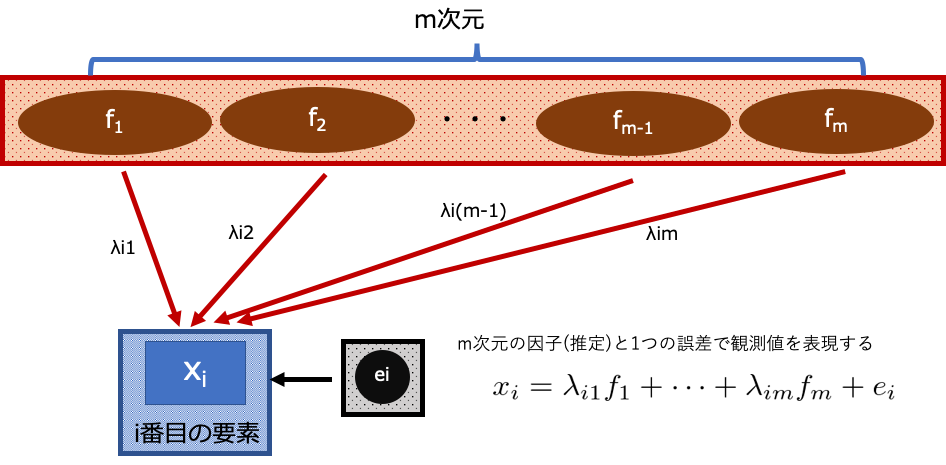
先の例を一般的にかくと下記のようになります.
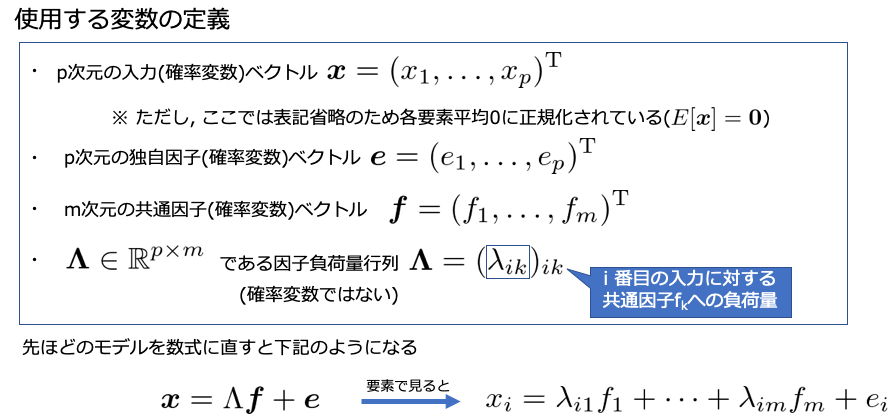
変数の定義
共通因子
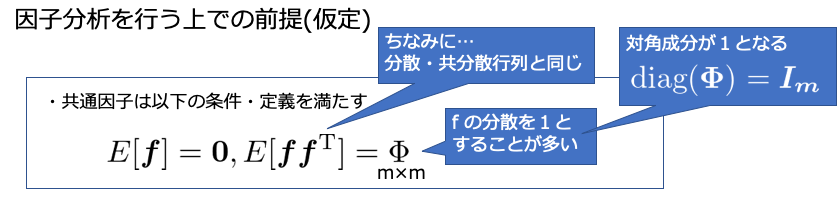
また,共通因子 $ \bf{f} $ の満たすべき性質して以下のようなものがあります.期待値が $ \bf{0} $ で,分散共分散行列が $\bf{\Phi} $ とする.ここで$\bf{\Phi} $は対角成分(分散)を$ \bf{I}_m$ とすることが多いみたいです.
潜在因子
潜在因子に関しては以下のような仮定をおきます.基本的には,分散共分散行列が対角行列になるというもので,対角成分以外は0になります.

共通因子と潜在因子の関係
共通因子と潜在因子は,互いに共分散が0になり,仮に正規分布に従っていると仮定すれば,互いに独立な関係にあるということです.
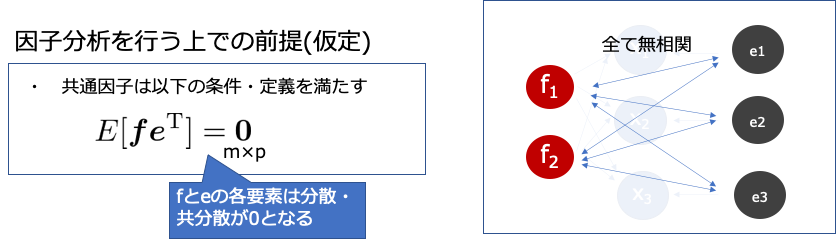
直交モデルと斜交モデル
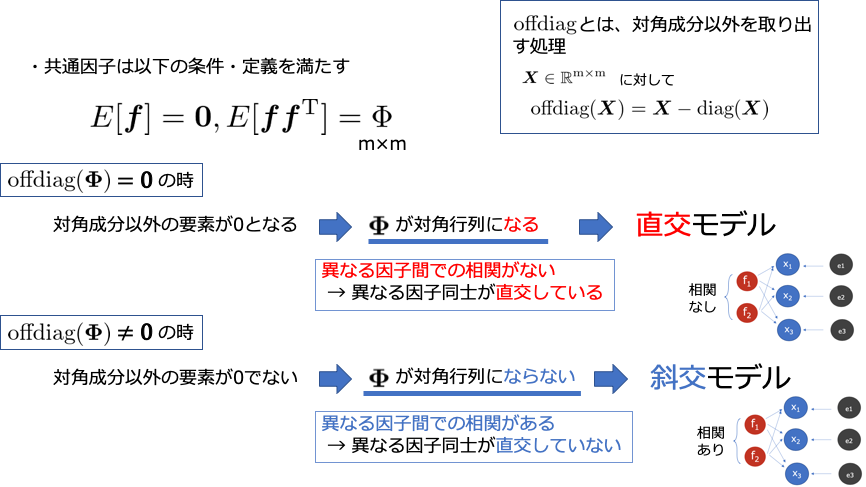
直交モデルや斜交モデルというのは先ほど出てきた共通因子の分散共分散行列$\bf{\Phi} $にどの仮定をおくのかという問題になってきます.つまり対角成分以外の要素が0なのかどうかというのが大切になってきます.これは潜在因子同士の相関関係をどれだけ仮定するのかという話になり,直交モデルの場合は,対角成分以外は0になり,異なる因子同士の相関がない前提で話が進むということです.
独自性と共通性
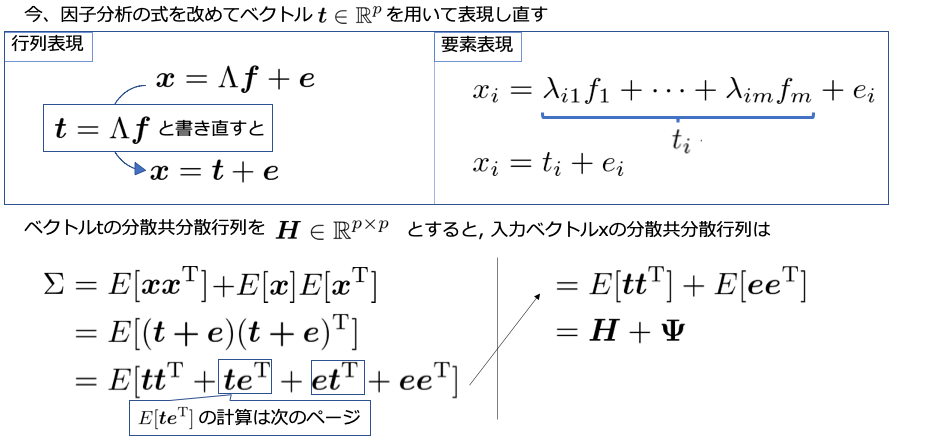
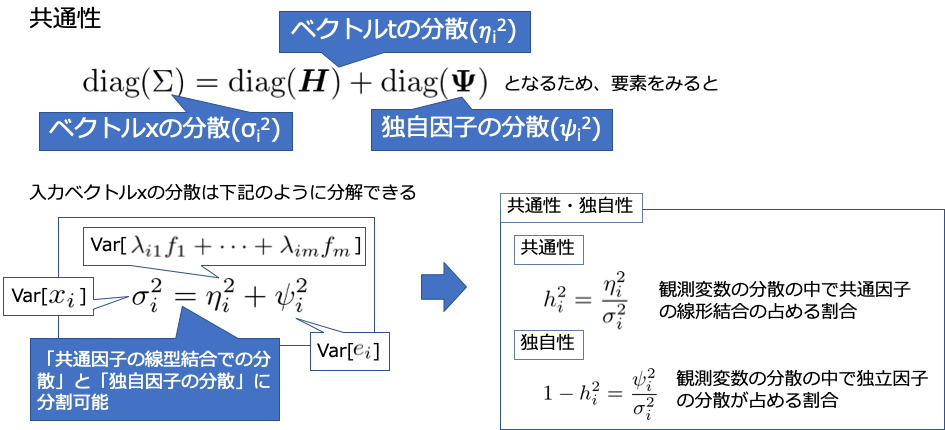
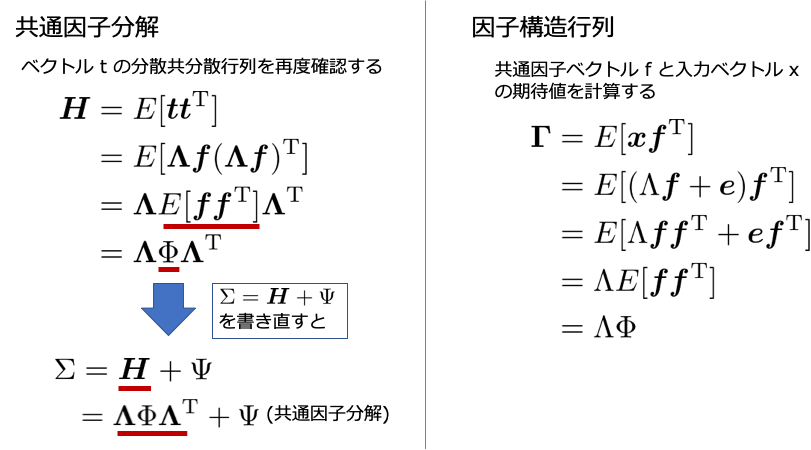
独自性と共通性について説明していきます.少し,その前に必要となる変数tについて説明していきます.こちらは,観測変数を共通因子で説明される箇所と独自因子で説明される箇所に分解した場合に,前者に当たる部分をまとめたものです.このtの分散共分散行列を改めて $ \bf{H}$とおくと,実は観測変数の分散共分散行列$ \Sigma$は,tの分散共分散行列$ \bf{H}$と,独自因子の分散共分散行列 $ \Psi $に分解できることに気がつきます.
この性質から,それぞれの対角成分をそれぞれ共通性,独自性と定義します.
共通因子分解と因子構造行列
先ほど突然変数tというものが出てきて,改めて因子負荷量行列 $ \bf{\Lambda} $と共通因子ベクトル $ \bf{f} $の関係を整理すると下記の左側のような関係が得られるととがわかります.これを共通因子分解と呼びます.
また,右側の因子構造行列は,観測変数$ \bf{x} $と共通因子ベクトル $ \bf{f} $の行列積の期待値を計算したものになります.今度出てくることがあるので頭の片隅においておいていただければと思います.
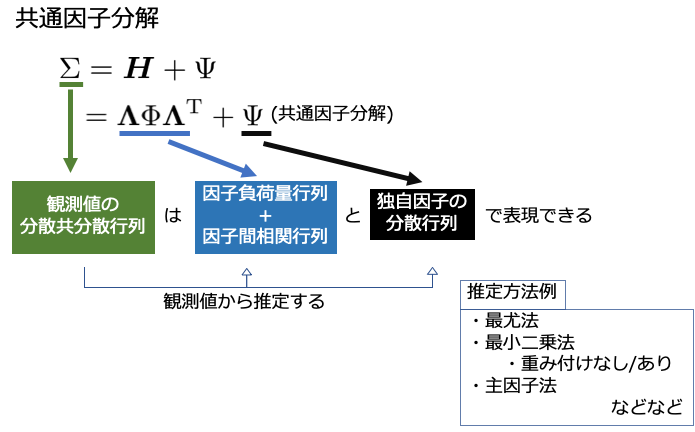
実は,先ほど出てきた共通因子分解を改めて見ると,観測変数の分散共分散行列は,因子負荷量行列と因子間分散共分散行列(相関係数行列)と独自因子の分散行列に分解できることに気がつきます.
SPSSなどで指定できる主因子法や最尤法は,実はこちらのように,どのように共通因子分解の各要素を推定するのかという手法になっていることがわかると思います.
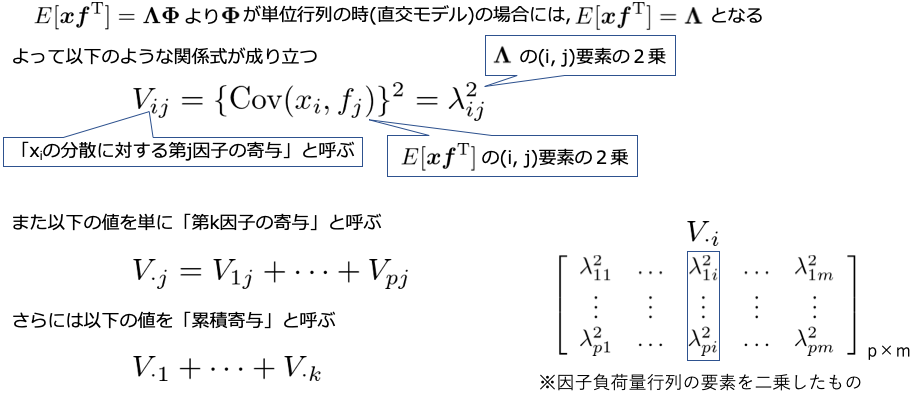
因子寄与率
因子分析とよく並び話されることが多い主成分分析では,寄与率は丁度固有値の累積和の比によって計算できるのは周知の事実だとは思いますが,因子分析はそう簡単にはいきません.その理由を説明していきます.(と言ってもスライドのコピペですが...)
つまり,直交モデルのように$ \text{Var}(\bf{f})^{-1}$ が単位行列になることがわかっている場合には,因子負荷量の2乗和によって簡単に求めることができます.しかし,斜交モデルの場合は,計算自体はできますが,結局それってなんの値なの?みたいな状態になると思います.これをいかんと解釈するかは流派が複数あるらしいのでここでは触れませんが,斜交モデルの場合は注意が必要なことは念頭におくと良いのかもしれません.
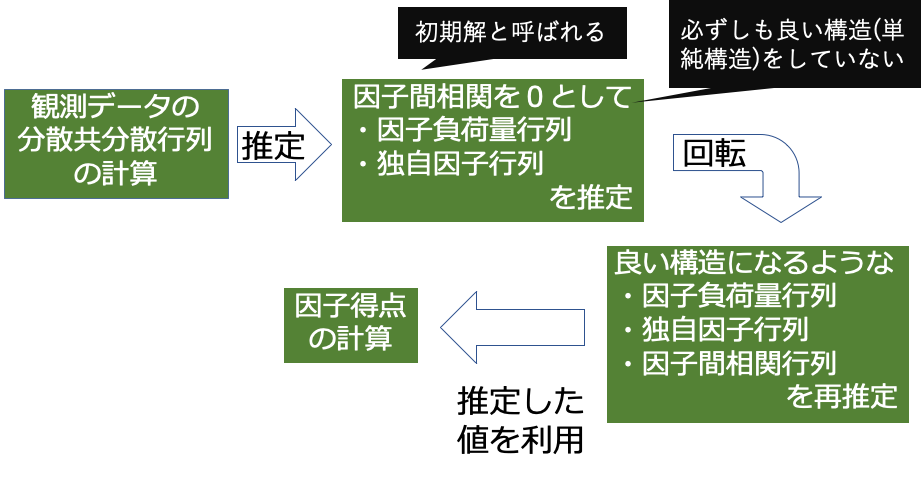
因子分析の俯瞰図
こちらは因子分析の計算の流れを書いたものです.あくまでこれまで述べてきた内容はあくまで概要と定義ですので,細かい推定方法は後々追記していきたいと思います.(因子分析は奥が深い...)
補足
今回お話した内容は下記のページあります.興味のある方はご覧いただければと思います.
重回帰分析と因子分析の概要
参考文献
書籍/論文
(こちら個人的に一番お勧めです)因子分析 (シリーズ行動計量の科学) 市川雅教 著
因子分析―その理論と方法 (統計ライブラリー) 柳井晴夫 ・繁桝算男 ・前川眞一 ・市川雅教 著
因子分析法〔第2版〕 芝 祐順 著
因子分析法通論 浅野 長一郎 著
意味がわかる多変量解析 石井 俊全 著
因子分析における統計的推測:最近の発展 狩野 裕, 行動計量学, 1990 年, 18巻, 1号 p.3-12
ネットのサイト
因子数決定法,斜交回転法,階層因子分析 香川大学経済学部, 堀 啓造
日心2000ワークショップ 心理学の基礎(6) 因子分析の基本問題
探索的因子分析リンク集(日本語中心)