目次
- はじめに
- 決定木とは
- データの準備
- 実験
- 結論
はじめに
yamayafumiteru(https://twitter.com/yamayafumiteru) です。
機械学習でLightGBMを活用するケースをよく見るようになりました。
自分もLighGBMを使う機会があり、決定木は、「特徴量の大小関係を見ているので、値が等倍されても結果が変わらない」ということを目にしました。
本当かな?と疑問に思ったので検証してみることにします。
今回は、標準正規分布に従う乱数のfeature1とfeature2を用意し、片方の特徴量を1000倍した際に結果が変わるかを検証します。
決定木とは
決定木とは、分類木と回帰木を組み合わせたもので、ツリーによってデータを分析する手法です。
やりたいことが分類のときは、分類木を使い、やりたいことが数値の予測なら回帰木を使います。
以下の記事がわかりやすかったので画像と説明を引用します。
参考記事)決定木、分類木、回帰木の意味と具体例
分類木の例です。
温度と湿度のデータ、および、その日A君が暑いと感じたか暑くないと感じたかのデータが与えられた状況を考えてみます。
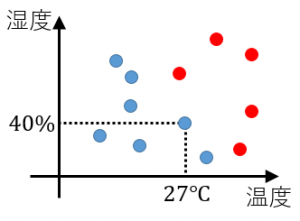
図の1つの点が1日を表します。赤い点はA君が暑いと感じた日、青い点は暑くないと感じた日を表します。
例えば、温度が 27度で湿度が 40%の日は暑くないと感じています。
このデータから、例えば、下図のような温度と湿度がどのようなときに暑いと感じるのか?を表現したツリーを作ることができます。
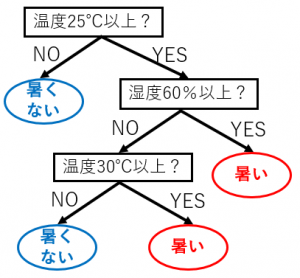
この分類木をもとのデータ図に境界線を追加して表現することもできます。
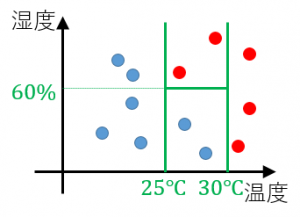
なお、この例は二値分類ですが、3つ以上のグループの分類問題にも有効なモデルです。
データの準備
# ランダムなデータ100件を作成する。
import lightgbm as lgb
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
from lightgbm import plot_tree
# サンプルデータの作成
np.random.seed(42)
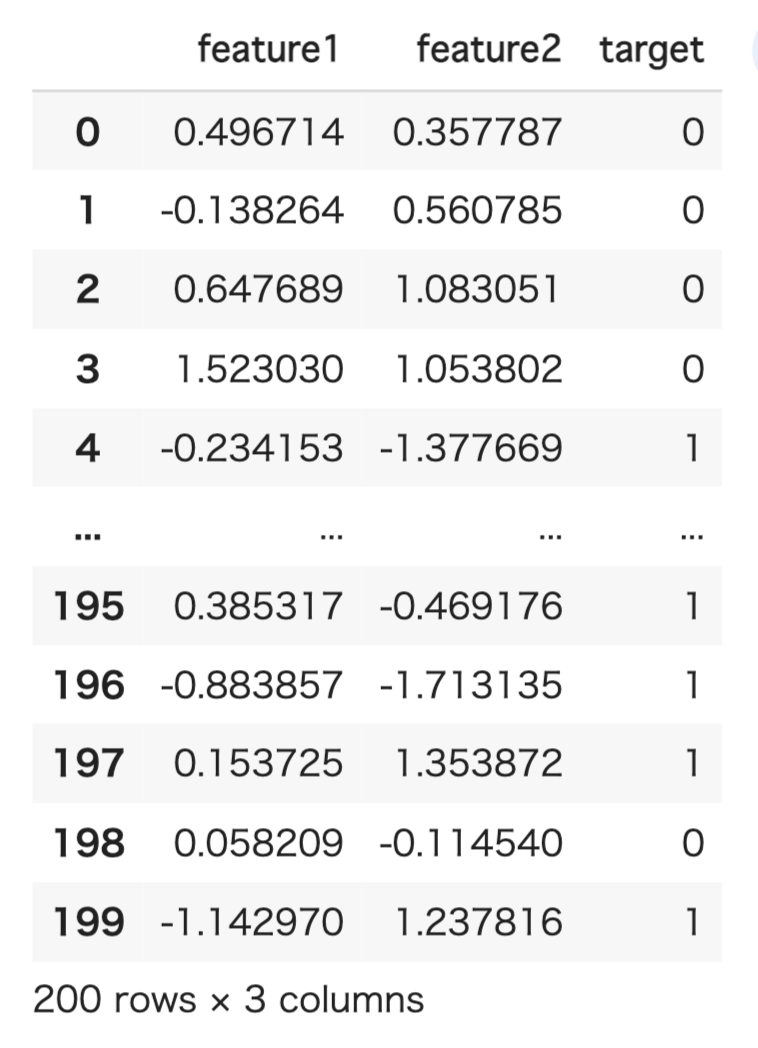
df = pd.DataFrame({'feature1': np.random.randn(200), 'feature2': np.random.randn(200), 'target': np.random.randint(0, 2, 200)})
実験
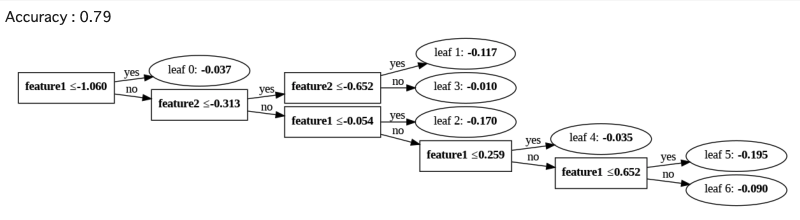
# 特徴量を1000倍しないパターン
df['feature1'] = df['feature1'].values
df['feature2'] = df['feature2'].values
# モデルの構築
model = lgb.LGBMClassifier()
# モデルのトレーニング
model.fit(df[['feature1', 'feature2']], df['target'])
# 決定木の可視化
plot_tree(model, tree_index=0, figsize=(10,10))
# モデルの予測
predictions = model.predict(df[['feature1', 'feature2']])
# 精度の計算
accuracy = accuracy_score(df['target'], predictions)
print('Accuracy:', accuracy)
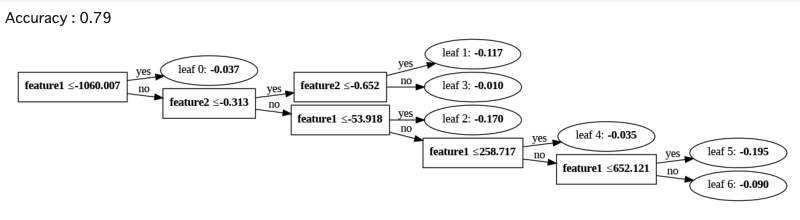
# 特徴量を片方だけ1000倍する
df['feature1'] *= 1000
df['feature2'] = df['feature2'].values
# モデルの構築
model = lgb.LGBMClassifier()
# モデルのトレーニング
model.fit(df[['feature1', 'feature2']], df['target'])
# 決定木の可視化
plot_tree(model, tree_index=0, figsize=(10,10))
# モデルの予測
predictions = model.predict(df[['feature1', 'feature2']])
# 精度の計算
accuracy = accuracy_score(df['target'], predictions)
print('Accuracy:', accuracy)
結論
特徴量を1000倍しても互いにAccuracy0.79という結果になりました。片方だけ特徴量を1000倍した場合でも、木の形は変わらないという結果になりました。
間違いがありましたら、お手数ですがご指摘いただけますと幸いです。
また、今回記事を作成するにあたり参考にした記事も記載します。ご参考くださいmm
参考文献
https://nnkkmto.hatenablog.com/entry/2020/12/15/000000
https://mathwords.net/ketteigi