Turbowarpでnandgameのcpuを再現してみた

注意
この記事はnand gameのネタバレ(答え)を含みます。

1 きっかけ

cpuの勉強をしたくてnand gameで遊んでいたところ 「これTurbowarpでも作れんじゃね」と思い勉強の実践も兼ねて作ってみることにした。

turbowarpには『ビット操作』という便利な拡張機能があるが負の値を-111111...と表現してしまうので16bitの論理ゲートなどは1bitずつ変換してくっつけたもので表すことにする。

2.今回作るcpuの構造

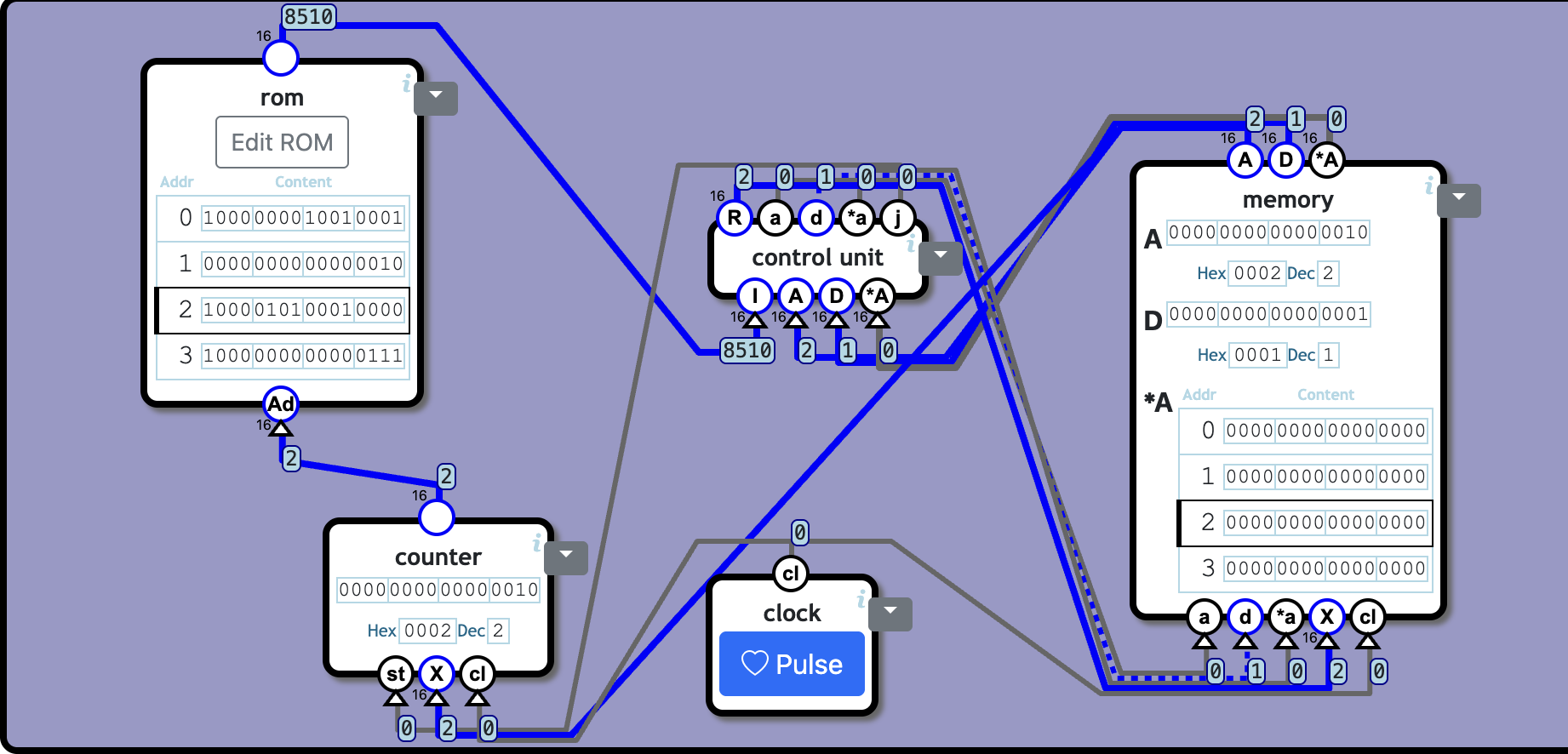
主に、RAM、コントロールユニット、クロック回路、カウンター、rom　でできている
(めっちゃわかりにくい)

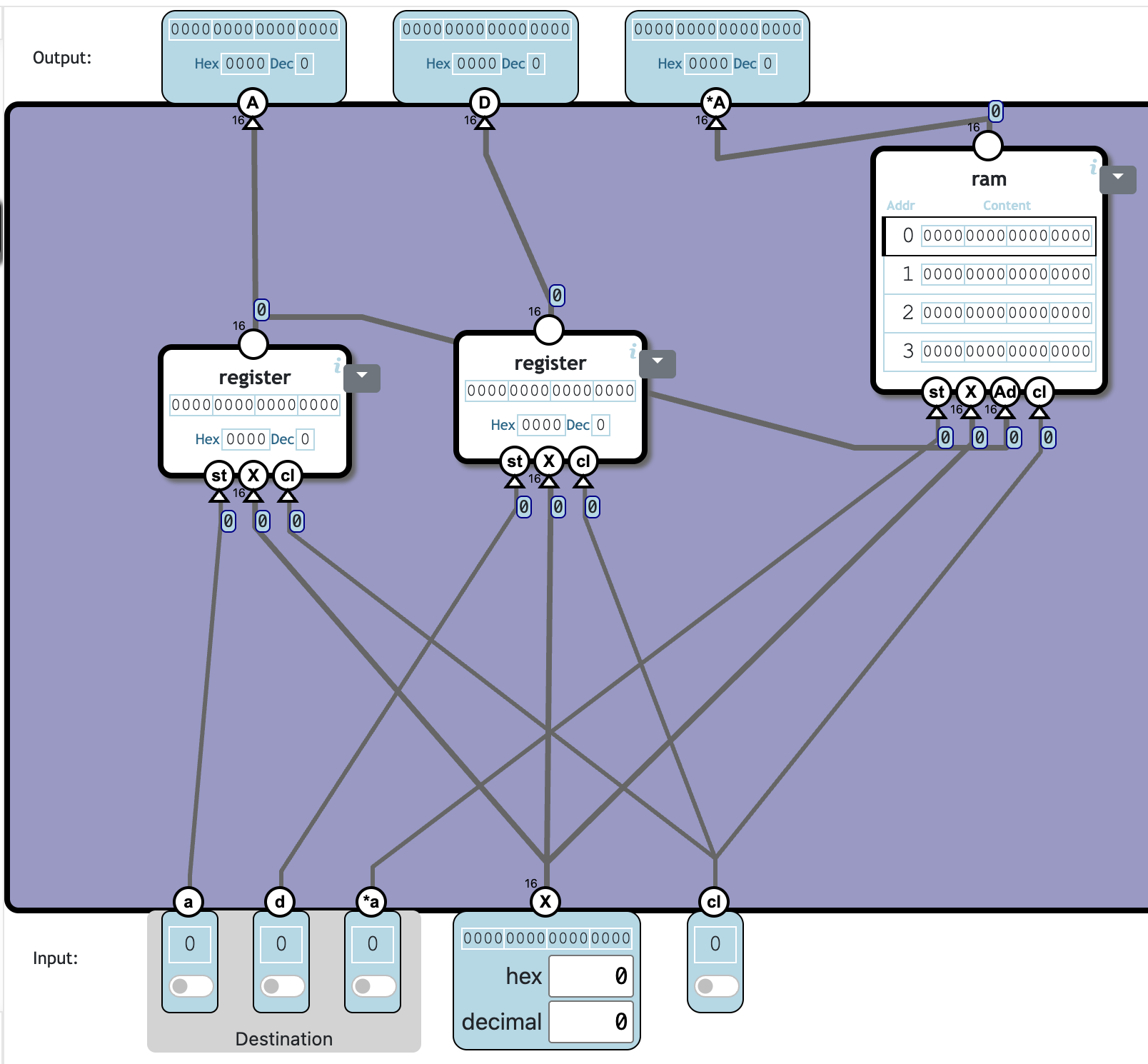
2.1 memory

このmemoryは二つのレジスタと一つのRAMでできているようだ。

これをさらに分解していく

register

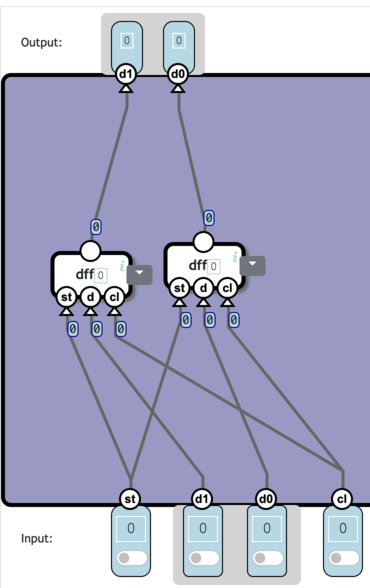
N bitレジスタはDFFがN個でできているようだ。　(この場合はN=2)
しかし画像中のD-FFはDラッチを使用していて、そのDラッチは出力を入力に代入するという方法でできているので今の私の技術力では再現することができない...

なので私は、レジスタをブロックで直接作ることにした。
そして完成したのがこれだ。

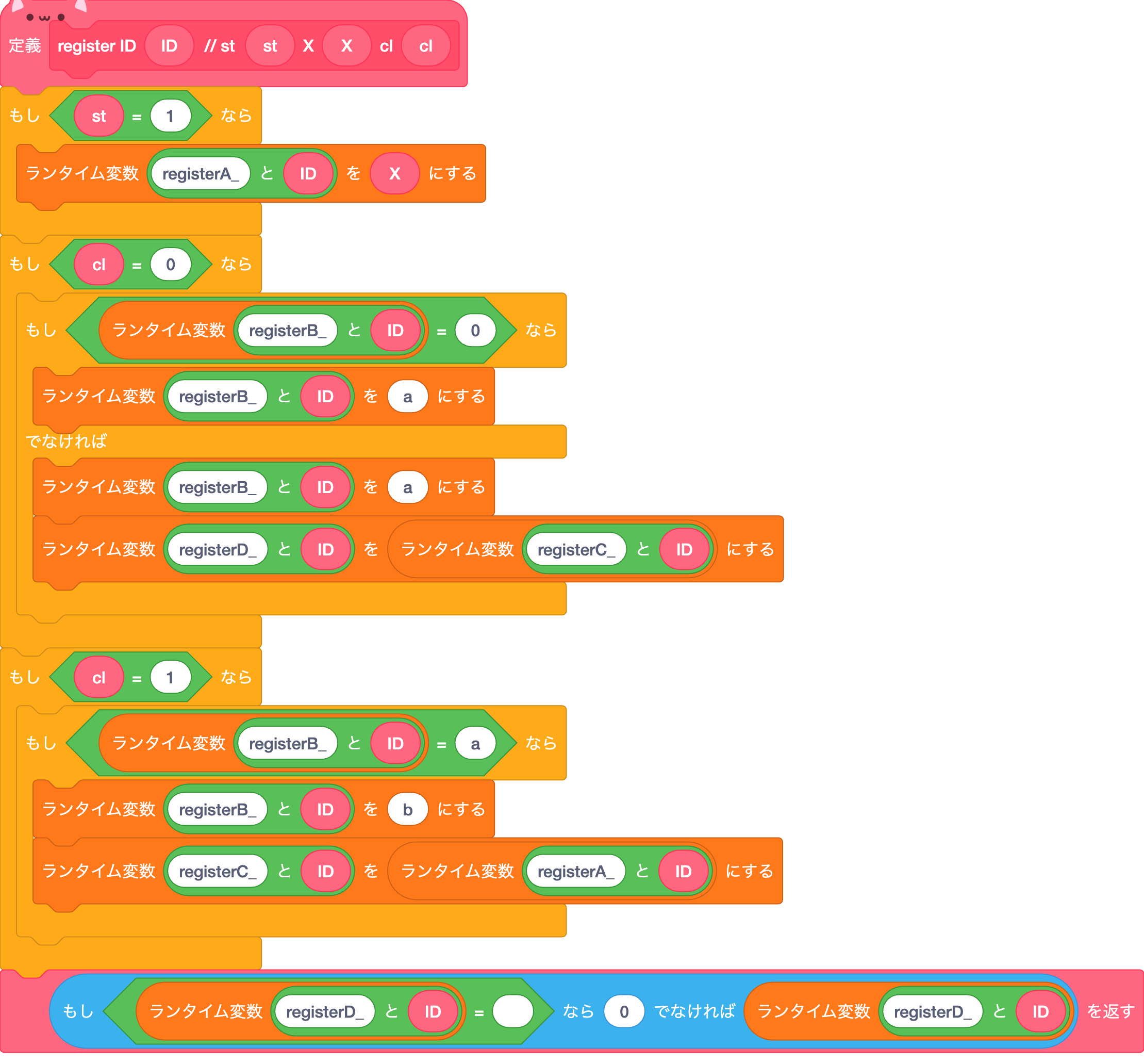
このIDというものは複数のレジスタを区別する役割がある。

一応これでもちゃんとnandgameと同じように動作する。

途中で値が変わっても一番最初に記録した値が出る。
説明;
registerA_---1番最初の入力を記録する変数

registerB_---値をセットしたか（clが1の時,registerC_を変更しないようにするため）

registerC_---値をセットしたときregisterA_を記録する変数

registerD_---出力用の変数(registerC_を出力)

2.2 RAM

RAMはいくつものレジスタを組み合わせてできている。
いちいちレジスタを何個も組み合わせて作るのは効率が悪い(めんどい)ので
これも一から作っていく

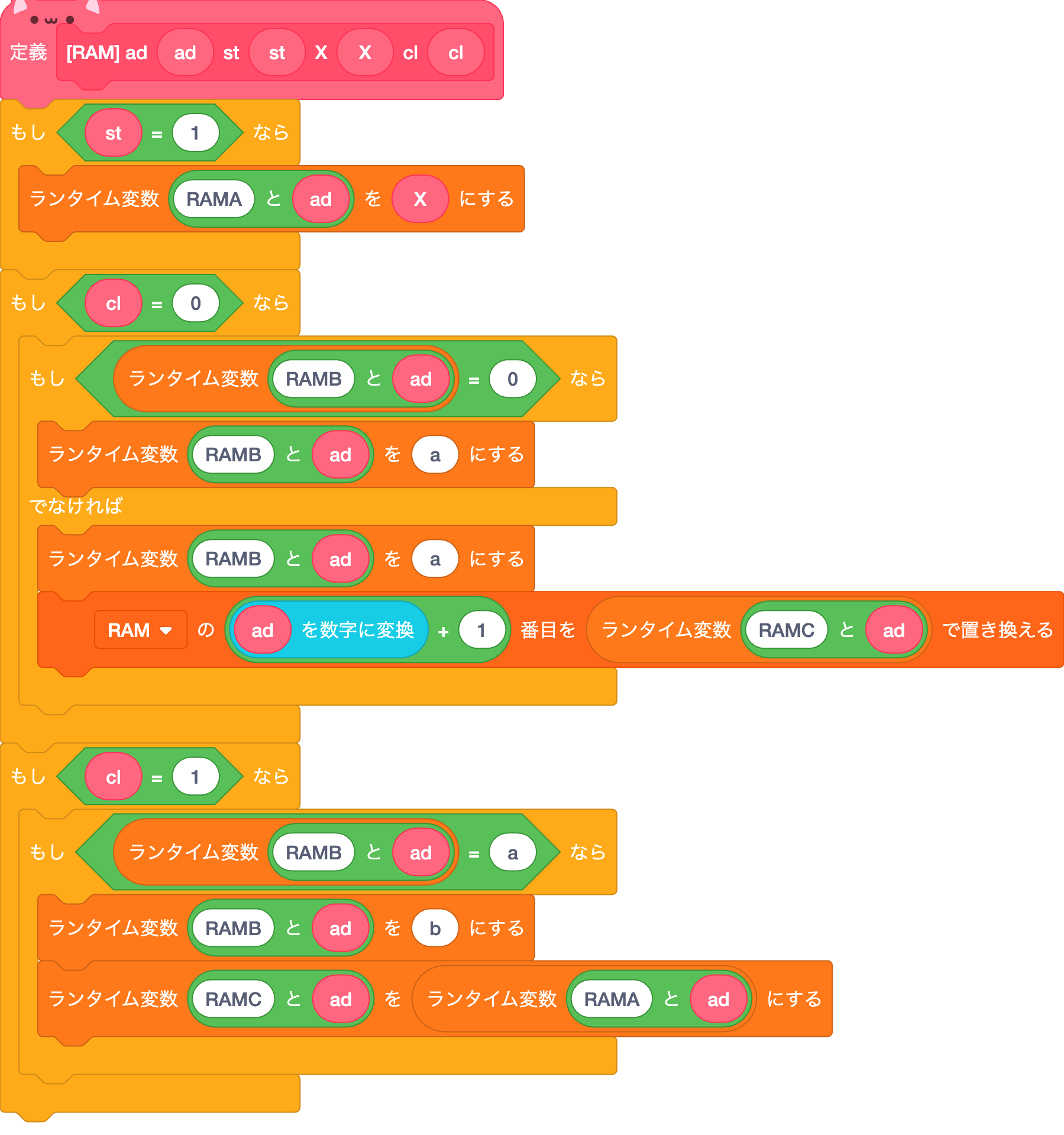
今回は保存、出力先をRAMというリストにしてみた。
registerのブロックの出力先(register_D)を リストRAMにしただけ。
仕組みは同じ。

2.3 counter

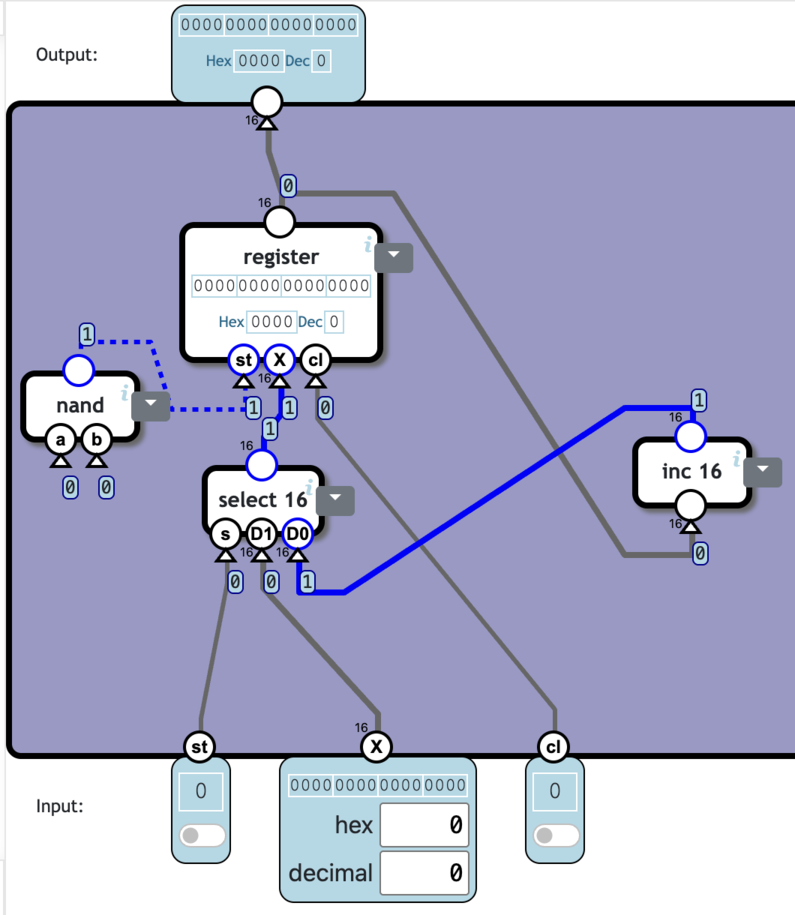
見ての通りカウンターも一部出力を入力に代入しているところがあるので一から作った。
結果↓

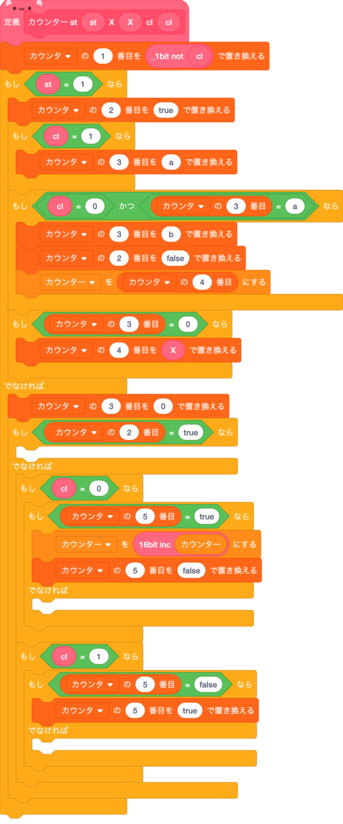
説明;
カウンタ1 特に意味はない　制作過程で出てきたやつ　今は修正済み。

カウンタ2 Xを書き込み中か(clが更新されたか)

カウンタ3モード判別
0の時インクリメントモード
a,bの時setモード

カウンタ4 Xの値の保存

カウンタ5 カウンタに書き込み可能か(clが更新されたか)

2.4 control unit

さぁここからが本番だ。
control unitはCPUにとって心臓部なのでパーツも多いし複雑になってくる。
なので、重要なもののみを解説することにする。

ここはわかりやすいように本来の順番で解説していこう。

論理ゲート

どれも基本的な仕組みは同じだ。 最初にも言った通り一つひとつ変換して出力する。

説明;

〇〇出力
〇〇 counter変換するビット
〇〇 answer変換結果

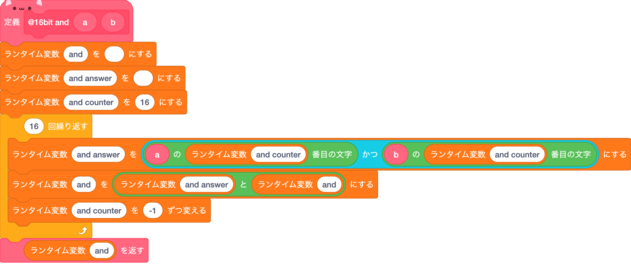
and

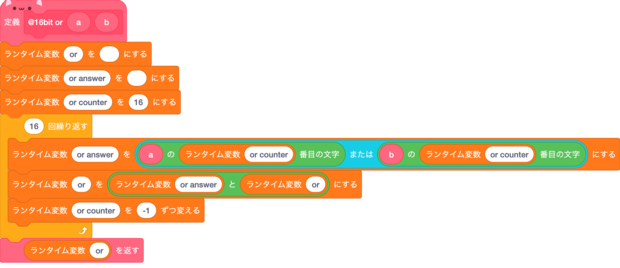
or

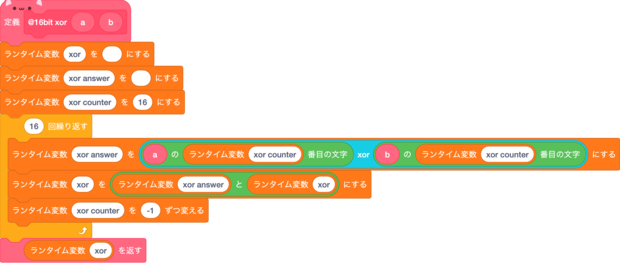
xor

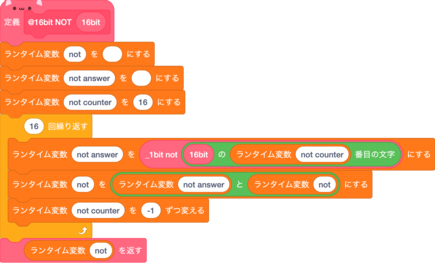
not

---

計算

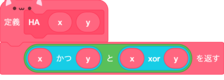
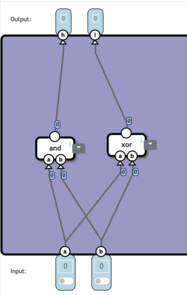
HA

半加算機(Half Adder)は1ビットの2つの入力された値を加算、出力(2ビット)する回路だ。

これを再現している↓

FA

全加算機(Full Adder)は2つの入力された値と繰り上げ(両方1ビット)を加算、出力(2ビット)する回路だ。

半加算機が三つでできる(頑張れば二つで行けるらしい)

非常にわかりにくい。
丁寧によんでいけばこうなっているとわかるだろう。

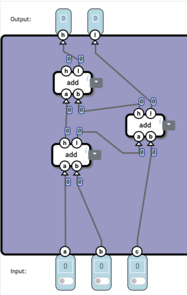
ちなみに、
x=a
y=b
z=c
である。

MA

多ビット加算器(Multi-bit Adder)は多数のビットを加算、出力する回路である。

今回は16ビットcpuなので16個必要だ。
しかし、ram同様いちいちパーツを組み合わせて作るのは効率が悪い(めんどい)のでこれも一から作っていく。↓

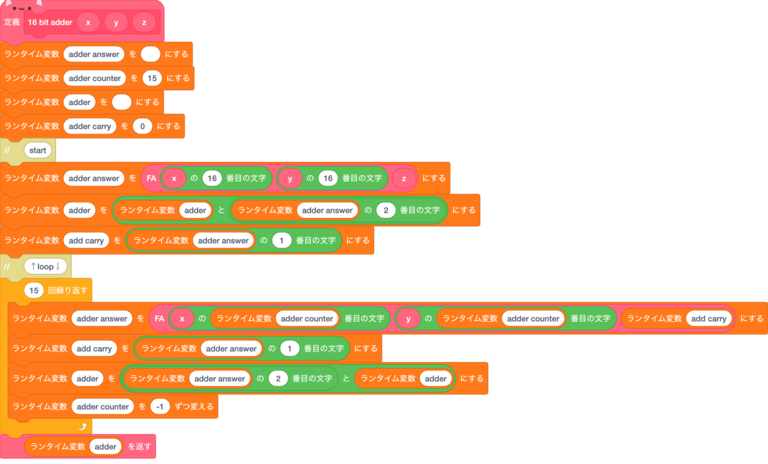
説明;
adder answer :1ビット加算機の結果
adder counter:何ビット目を計算するか
adder :出力
adder carry :「1ビット加算機の結果」の繰り上げの値
手順;
//start
①16ビット目を加算する。adder carryを設定する。
//↑loop↓
②15ビット目、adder carryを加算する。　adder carryを更新する。
③14ビット目、adder carryを加算する。　adder carryを更新する。
④13ビット目、adder carryを加算する。　adder carryを更新する。
...(1ビット目まで繰り返す)

Increment

インクリメントは入力された数+1を出力する回路だ。
加算機を利用している。

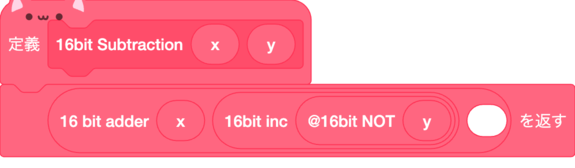
Sub

Subtraction(減算)はX-Yの結果を出力する回路だ。
これの考え方を変えるとX+(-Y)となり加算器と2の補数を使って結果を出すことができる。
2の補数とは、二進数で負の数を表す代表の方法である。
2の補数は負の数にしたい値を反転(not)して1を足せばできる。

参考https://www.seplus.jp/dokushuzemi/ec/fe/fenavi/kind_basic_theory/basic-theory2/

EZ(eq)

Equal to Zeroの略でX=0の時1を出力する回路だ。

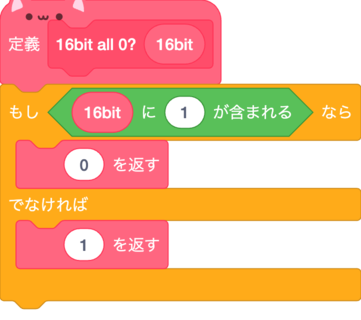
LZ(lt)

Less than Zeroの略でX<0の時1を出力する回路だ。

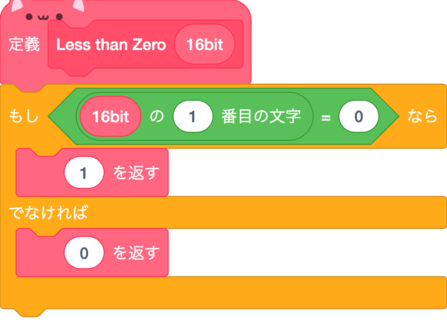
第15ビットを符号ビットとして利用している。
符号ビットが1の時は数値が負の数だということを表している。

---

切り替え&スイッチ

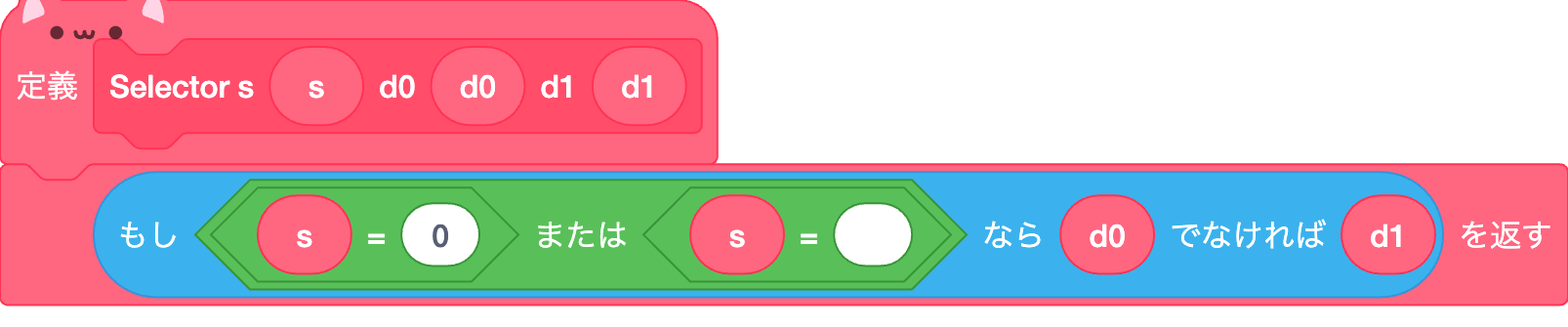
セレクタ

セレクターはsが1の時d1を、0の時d0の値を出力する回路である。

スイッチ

スイッチはsが1の時dの値をc1に、0の時dの値をc0に出力する回路である。
(今回はc1、c0を一つの値としてまとめた)

---

演算装置

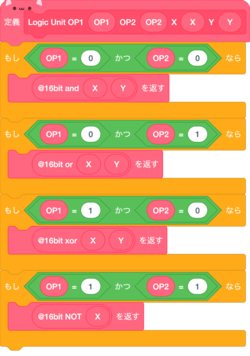
ビット演算装置

このビット演算装置の入力は二つのオペコード(op0,op1)と二つの16ビットの値(X,Y)の4つで構成されていて出力は、一つだけである。

入出力の関係は以下のようになる。

op1	op0	出力(j)
0	0	X AND Y
0	1	X OR Y
1	0	X XOR Y
1	1	Xをビット反転

これをturbowarpで実装するとこうなる

算術演算装置

この算術演算装置の入力も二つのオペコード(op0,op1)と二つの16ビットの値(X,Y)の4つで構成されていて出力は、一つだけである。

op1	op0	出力(R)
0	0	X + Y
0	1	X - Y
1	0	X + 1
1	1	X - 1

これをturbowarpで実装するとこうなる

算術論理演算装置(ALU)

この算術論理演算装置はさっき紹介した二つの演算装置を一つにまとめたもので、入力は二つのオペコード(op1,op0),二つのフラグ(sw,zx),回路選択用の入力(u)の5つから構成されていて、出力は一つだけである。
uが1の時は算術演算装置の結果を、0の時はビット演算装置の結果を出力する。
これをturbowarpで実装すると...?

(自分で作ったのに意味わからん)

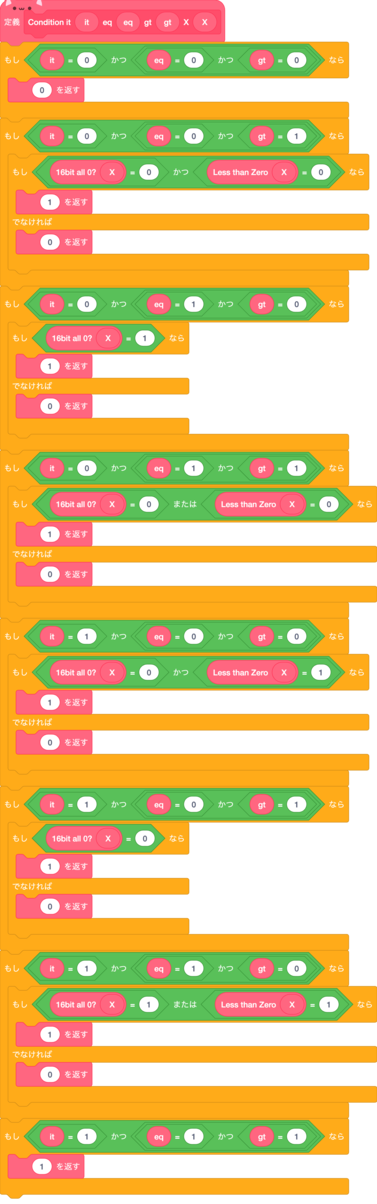
条件(condition)

この『条件』は最大3つのフラグを使用してXがそのフラグの条件を全て満たしているかを判断する回路だ。

フラグ	条件
lt	0未満
eq	0と等しい
gt	0より大きい

わかりやすくするために例を挙げよう
X ≧ 0　の時1を出力させたい場合eqとgtを1にすればいい
(≧を分解すると=と>に分かれ、それを条件とするフラグはeqとgtしかないためだ)

lt	eq	gt	1を出力する条件
0	0	0	絶対に出力は0
0	0	1	X > 0
0	1	0	X = 0
0	1	1	X ≧ 0
1	0	0	X < 0
1	0	1	X ≠ 0
1	1	0	X ≦ 0
1	1	1	絶対に出力は1

これをturbowarpで実装するとこうなる(今気づいたけどltがitになっている↓)

3.おまけ

1.今回使用した拡張機能

・ビット操作
・Lilyの道具箱
・カスタム定義

2.実際にできたcpu(+エディター)のファイル
[製作中]

3.機械語の解説
cpu機械語解説メモ

4.終わりに

今回はnand gameのHardwareレベルをクリアして学んだことを活かしてこの作品(CPU)を作ったが、今度はSoftwareレベルをクリアしてこの作品をもっとアップデートしていきたいと思っている。

最後まで見てくれてありがとうございました。