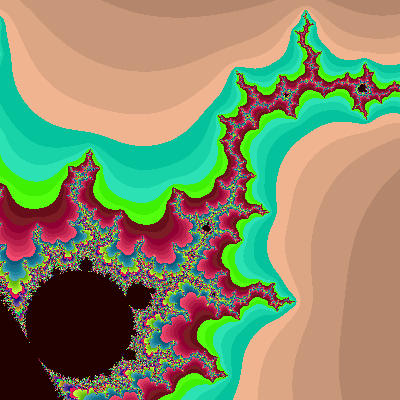
描画範囲: (-1.30 <= x <= -1.10, 0.20 <= y <= 0.40)
... オリジナルコードの例と同じ範囲。
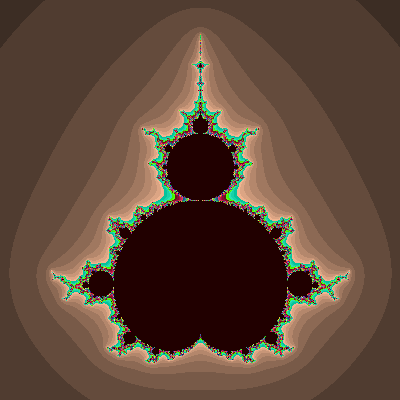
描画範囲: (-2.25 <= x <= 0.75, -1.50 <= y <= 1.50)
... よく見るやつ(が90度回転してる)。

描画範囲: (0.40 <= x <= 0.44, 0.30 <= y <= 0.34)
... 長崎あたりの地形みたい。
マンデルブロ集合って?
こんなの: Wikipedia - マンデルブロ集合
数学的な特性を説明できるほどは知らない。かっこいい絵が得られるのは知ってる。ふしぎ。
お手本にしたコードがあります
筑波大学 生物資源学類の奈佐原先生のサイトより:
コンピュータ・グラフィックス(CG)入門 - フラクタル図形を描く
上記リンク先のコードはC言語 + EGGXというグラフィックライブラリで記述されています。
上記リンク先のコードをそっくりそのままPython + OpenCVで書き直しました。俺の功績はほぼ0 1。
コード
- Wを書き換えると描画サイズが変わります。
- X0,X1,Y0,Y1を書き換えると描画範囲が変わります。
import numpy as np
import cv2
import math
from tqdm import tqdm
W = 400
X0 = -1.30
X1 = -1.10
Y0 = 0.20
Y1 = 0.40
LIMIT = 20.0
INF = 300
def csquare(x, y):
xx = x*x - y*y
yy = 2.0 * x * y
return xx, yy
def cabs(x, y):
cabs = math.sqrt(x*x + y*y)
return cabs
if __name__ == '__main__':
dx = (X1 - X0) / W
dy = (Y1 - Y0) / W
img = np.zeros((W, W, 3), np.uint8)
pbar = tqdm(total = W*W)
cx = X0
cy = Y0
for x_fig in range(0, W):
for y_fig in range(0, W):
x = 0.0
y = 0.0
n = 0
while n < INF and cabs(x, y) < LIMIT:
sqr = csquare(x, y)
x = sqr[0] + cx
y = sqr[1] + cy
n = n + 1
# print(str(cx) + " " + str(cy) + " " + str(n))
r = n % (INF/11)
g = n % (INF/15)
b = n % (INF/19)
img.itemset((x_fig, y_fig, 0), 12*b)
img.itemset((x_fig, y_fig, 1), 15*g)
img.itemset((x_fig, y_fig, 2), 20*r)
pbar.update(1)
cy = cy + dy
cy = Y0
cx = cx + dx
pbar.close()
cv2.imwrite("mandelbrot.png", img)
よくわからんかったこと
縦軸に対して反転している理由
このコードで出力した画像は、元コードで出力した画像を縦軸に対して反転した状態になります。
これはEGGXの座標系とOpenCVの座標系の差異に由来する……と思っていたのですが、なんか変だ:
EGGXマニュアル: http://www.cse.kyoto-su.ac.jp/~oomoto/lecture/program/C/eggx_procall.pdf
グラフィックス画面の座標は,デフォルトでは左下が (0.0, 0.0) で右上が (xsize-1.0, ysize-1.0) になっています.
OpenCVの座標は、左上が(0,0)で、右下が(x,y)だから、横軸に対して反転するのが筋な気がするのだが……。
色味が若干違う理由
よくわからんかった。計算精度か、OpenCVとEGGXの色の取り扱いの違いか。
-
簡単にググった限り、Python3 + OpenCV3でカラーのマンデルブロ集合を描画している例は見つからなかったので微小な意義はあると思っている。モノクロ例:https://qiita.com/jabberwocky0139/items/33add5b3725204ad377f OpenCV2例: http://kenbell.hatenablog.com/entry/20120220/1330865077 ↩