概要
以前に{tensorflow}のPythonライブラリをimportする関数を用いてRからKerasを呼び出し、短歌生成を試みました。
しかしながら、試したものの知見が足らず、満足がいく結果が出せたとは言えません。
そこで今回はKerasのお勉強を兼ねて、Kerasのexampleにある画像生成(VAE; variational autoencoder)のスクリプトをRで書き換え、実行してみました。こうして得た知見を活用して、よりこなれた短歌生成を目指したいと思います。
加えて今回は、Pythonライブラリをimportするライブラリとして{reticulate}を用いました。こちらは{tensorflow}からPythonライブラリを読み込む機能が分けられたもので、{tensorflow}でも{reticulate}を使うようになりました。
さらに{reticulate}にはR上でPythonを参照するための様々な機能が追加されており、以前はできなかったこと(例えば、1要素のRベクトルをスカラーとしてアサインしようとするとPythonのリストに変換されてしまい、エラーになっていた)が可能になっています。
なお、本記事では「Kerasを用いたVAEのPythonスクリプトを、Rで実行するにはどういう風に記述するか」について書いております。VAEの理論については「参考」にあるリンクをご参照ください。
定義部
ライブラリとデータセット読み込み
library(tidyverse)
library(reticulate)
library(DiagrammeR)
# KerasをR上で使えるように{reticulate}のimport関数で読み込み
keras <- reticulate::import(module = "keras")
# モデルをdotに変換するKeras関数を別名で定義(関数名が長くなりすぎて視認性が悪かったため)
model_dot <- keras$utils$visualize_util$model_to_dot
データセット準備
mnist_d <- keras$datasets$mnist$load_data()
# 画像データを[0, 1]に変換
x_train <- array(
data = mnist_d[[1]][[1]] / 255,
dim = c(nrow(x = mnist_d[[1]][[1]]), cumprod(x = dim(x = mnist_d[[1]][[1]])[-1])[2])
)
x_test <- array(
data = mnist_d[[2]][[1]] / 255,
dim = c(nrow(x = mnist_d[[2]][[1]]), cumprod(x = dim(x = mnist_d[[2]][[1]])[-1])[2])
)
定数と関数の定義
RからKeras(Python)に整数値を渡す場合は明示的に整数値として定義する必要あります。ここでは数値の後ろに「L」をつけて整数値としていますが、複数まとめて整数化したいときはas.integerを用いてもいいです。
# モデルパラメータ
BATCH_SIZE <- 100L
ORIGINAL_DIM <- 784L
LATENT_DIM <- 2L
INTERMEDIATE_DIM <- 256L
EPSILON_STD <- 1.0
# Epoch数
NB_EPOCH <- 100L
テンソル同士の計算をR上で定義すると型変換やbackendの競合などが厄介だったので、ここではPython関数として定義しました。
損失関数への複数引数の渡し方は下記を参考にしています。
py_def <- reticulate::py_run_string(
code = "
import keras.backend as K
from keras import objectives
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape = (batch_size, latent_dim), mean = 0., std = epsilon_std)
return z_mean + K.exp(z_log_var / 2) * epsilon
def vae_loss(z_mean, z_log_var):
def loss(x, x_decoded_mean):
xent_loss = original_dim * objectives.binary_crossentropy(x, x_decoded_mean)
kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis = -1)
return xent_loss + kl_loss
return loss
",
convert = FALSE
)
# Python側の環境に定数定義
py_def$batch_size <- BATCH_SIZE
py_def$original_dim <- ORIGINAL_DIM
py_def$latent_dim <- LATENT_DIM
py_def$epsilon_std <- EPSILON_STD
モデル定義と学習
スクリプト例を参考にモデルの定義を粛々と行います。
メソッド呼び出しに「$__call__」を用いており、視認性がとても悪くなっています。ここをうまくできると使いやすくていいですが、対応方法がわからないので要調査です。
Variational AutoEncoder
x <- keras$layers$Input(batch_shape = list(BATCH_SIZE, ORIGINAL_DIM))
h <- keras$layers$Dense(output_dim = INTERMEDIATE_DIM, activation = "relu")$`__call__`(x = x)
z_mean <- keras$layers$Dense(output_dim = LATENT_DIM)$`__call__`(x = h)
z_log_var <- keras$layers$Dense(output_dim = LATENT_DIM)$`__call__`(x = h)
# 前述の定義部で定義したPython関数をLambdaレイヤーで使用する関数に指定する
z <- keras$layers$Lambda(py_def$sampling, output_shape = list(LATENT_DIM))$`__call__`(list(z_mean, z_log_var))
decoder_h <- keras$layers$Dense(output_dim = INTERMEDIATE_DIM, activation = "relu")
h_decoded <- decoder_h$`__call__`(z)
decoder_mean <- keras$layers$Dense(output_dim = ORIGINAL_DIM, activation = "sigmoid")
x_decoded_mean <- decoder_mean$`__call__`(h_decoded)
vae <- keras$models$Model(input = x, output = x_decoded_mean)
vae$compile(optimizer = "rmsprop", loss = py_def$vae_loss(z_mean, z_log_var), metrics = list("mse"))
# VAEモデルの要約出力
> vae$summary()
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_1 (InputLayer) (100, 784) 0
____________________________________________________________________________________________________
dense_1 (Dense) (100, 256) 200960 input_1[0][0]
____________________________________________________________________________________________________
dense_2 (Dense) (100, 2) 514 dense_1[0][0]
____________________________________________________________________________________________________
dense_3 (Dense) (100, 2) 514 dense_1[0][0]
____________________________________________________________________________________________________
lambda_1 (Lambda) (100, 2) 0 dense_2[0][0]
dense_3[0][0]
____________________________________________________________________________________________________
dense_4 (Dense) (100, 256) 768 lambda_1[0][0]
____________________________________________________________________________________________________
dense_5 (Dense) (100, 784) 201488 dense_4[0][0]
====================================================================================================
Total params: 404,244
Trainable params: 404,244
Non-trainable params: 0
____________________________________________________________________________________________________
# Kerasの関数を用いてモデルをdot化した後に{DiagrammeR}で可視化
# VAEモデル構成
> DiagrammeR::grViz(diagram = model_dot(model = vae, show_shapes = TRUE)$create(prog = "dot", format = "dot"))

# callback関数でTensorboardのオブジェクトを作成。引数にはログの出力先を指定
tb <- keras$callbacks$TensorBoard(log_dir = "./tensor_board/")
# callbacks引数に先のTensorboardオブジェクトを加えたRのlistを指定して学習を開始
> vae_hist <- vae$fit(
x = x_train, y = x_train, shuffle = TRUE, nb_epoch = NB_EPOCH, batch_size = BATCH_SIZE,
verbose = 1L, callbacks = list(tb)
)
Epoch 1/100
60000/60000 [==============================] - 12s - loss: 191.4784 - mean_squared_error: 0.0577
Epoch 2/100
60000/60000 [==============================] - 18s - loss: 170.3066 - mean_squared_error: 0.0508
Epoch 3/100
60000/60000 [==============================] - 15s - loss: 166.8076 - mean_squared_error: 0.0493
Epoch 4/100
60000/60000 [==============================] - 15s - loss: 164.6561 - mean_squared_error: 0.0483
Epoch 5/100
60000/60000 [==============================] - 14s - loss: 163.0909 - mean_squared_error: 0.0475
Epoch 6/100
60000/60000 [==============================] - 13s - loss: 161.8344 - mean_squared_error: 0.0469
Epoch 7/100
60000/60000 [==============================] - 12s - loss: 160.6972 - mean_squared_error: 0.0463
Epoch 8/100
60000/60000 [==============================] - 14s - loss: 159.6432 - mean_squared_error: 0.0458
Epoch 9/100
60000/60000 [==============================] - 13s - loss: 158.6979 - mean_squared_error: 0.0453
Epoch 10/100
60000/60000 [==============================] - 14s - loss: 157.8867 - mean_squared_error: 0.0449
Epoch 11/100
60000/60000 [==============================] - 13s - loss: 157.1553 - mean_squared_error: 0.0445
Epoch 12/100
60000/60000 [==============================] - 14s - loss: 156.5216 - mean_squared_error: 0.0442
Epoch 13/100
60000/60000 [==============================] - 14s - loss: 155.9646 - mean_squared_error: 0.0440
Epoch 14/100
60000/60000 [==============================] - 14s - loss: 155.4928 - mean_squared_error: 0.0437
Epoch 15/100
60000/60000 [==============================] - 14s - loss: 155.0626 - mean_squared_error: 0.0435
Epoch 16/100
60000/60000 [==============================] - 15s - loss: 154.6859 - mean_squared_error: 0.0433
Epoch 17/100
60000/60000 [==============================] - 14s - loss: 154.3239 - mean_squared_error: 0.0431
Epoch 18/100
60000/60000 [==============================] - 13s - loss: 154.0035 - mean_squared_error: 0.0430
Epoch 19/100
60000/60000 [==============================] - 13s - loss: 153.6581 - mean_squared_error: 0.0428
Epoch 20/100
60000/60000 [==============================] - 13s - loss: 153.3801 - mean_squared_error: 0.0427
Epoch 21/100
60000/60000 [==============================] - 14s - loss: 153.1392 - mean_squared_error: 0.0426
Epoch 22/100
60000/60000 [==============================] - 15s - loss: 152.8732 - mean_squared_error: 0.0425
Epoch 23/100
60000/60000 [==============================] - 14s - loss: 152.6677 - mean_squared_error: 0.0423
Epoch 24/100
60000/60000 [==============================] - 13s - loss: 152.4509 - mean_squared_error: 0.0422
Epoch 25/100
60000/60000 [==============================] - 13s - loss: 152.2459 - mean_squared_error: 0.0421
Epoch 26/100
60000/60000 [==============================] - 14s - loss: 152.0889 - mean_squared_error: 0.0421
Epoch 27/100
60000/60000 [==============================] - 13s - loss: 151.8911 - mean_squared_error: 0.0420
Epoch 28/100
60000/60000 [==============================] - 12s - loss: 151.7171 - mean_squared_error: 0.0419
Epoch 29/100
60000/60000 [==============================] - 12s - loss: 151.5549 - mean_squared_error: 0.0418
Epoch 30/100
60000/60000 [==============================] - 12s - loss: 151.4016 - mean_squared_error: 0.0417
Epoch 31/100
60000/60000 [==============================] - 12s - loss: 151.2778 - mean_squared_error: 0.0417
Epoch 32/100
60000/60000 [==============================] - 12s - loss: 151.1159 - mean_squared_error: 0.0416
Epoch 33/100
60000/60000 [==============================] - 12s - loss: 151.0022 - mean_squared_error: 0.0415
Epoch 34/100
60000/60000 [==============================] - 12s - loss: 150.8492 - mean_squared_error: 0.0414
Epoch 35/100
60000/60000 [==============================] - 13s - loss: 150.7255 - mean_squared_error: 0.0414
Epoch 36/100
60000/60000 [==============================] - 15s - loss: 150.5891 - mean_squared_error: 0.0413
Epoch 37/100
60000/60000 [==============================] - 14s - loss: 150.5213 - mean_squared_error: 0.0413
Epoch 38/100
60000/60000 [==============================] - 14s - loss: 150.3956 - mean_squared_error: 0.0412
Epoch 39/100
60000/60000 [==============================] - 16s - loss: 150.2792 - mean_squared_error: 0.0412
Epoch 40/100
60000/60000 [==============================] - 15s - loss: 150.1885 - mean_squared_error: 0.0411
Epoch 41/100
60000/60000 [==============================] - 15s - loss: 150.0715 - mean_squared_error: 0.0411
Epoch 42/100
60000/60000 [==============================] - 13s - loss: 149.9864 - mean_squared_error: 0.0410
Epoch 43/100
60000/60000 [==============================] - 13s - loss: 149.8985 - mean_squared_error: 0.0410
Epoch 44/100
60000/60000 [==============================] - 13s - loss: 149.7982 - mean_squared_error: 0.0409
Epoch 45/100
60000/60000 [==============================] - 14s - loss: 149.7250 - mean_squared_error: 0.0409
Epoch 46/100
60000/60000 [==============================] - 12s - loss: 149.6136 - mean_squared_error: 0.0408
Epoch 47/100
60000/60000 [==============================] - 13s - loss: 149.5333 - mean_squared_error: 0.0408
Epoch 48/100
60000/60000 [==============================] - 13s - loss: 149.4482 - mean_squared_error: 0.0407
Epoch 49/100
60000/60000 [==============================] - 15s - loss: 149.3567 - mean_squared_error: 0.0407
Epoch 50/100
60000/60000 [==============================] - 14s - loss: 149.2792 - mean_squared_error: 0.0407
Epoch 51/100
60000/60000 [==============================] - 14s - loss: 149.2187 - mean_squared_error: 0.0406
Epoch 52/100
60000/60000 [==============================] - 15s - loss: 149.1258 - mean_squared_error: 0.0406
Epoch 53/100
60000/60000 [==============================] - 14s - loss: 149.0511 - mean_squared_error: 0.0405
Epoch 54/100
60000/60000 [==============================] - 13s - loss: 148.9863 - mean_squared_error: 0.0405
Epoch 55/100
60000/60000 [==============================] - 14s - loss: 148.9004 - mean_squared_error: 0.0405
Epoch 56/100
60000/60000 [==============================] - 14s - loss: 148.8643 - mean_squared_error: 0.0404
Epoch 57/100
60000/60000 [==============================] - 12s - loss: 148.7888 - mean_squared_error: 0.0404
Epoch 58/100
60000/60000 [==============================] - 12s - loss: 148.6941 - mean_squared_error: 0.0404
Epoch 59/100
60000/60000 [==============================] - 12s - loss: 148.6297 - mean_squared_error: 0.0403
Epoch 60/100
60000/60000 [==============================] - 12s - loss: 148.5614 - mean_squared_error: 0.0403
Epoch 61/100
60000/60000 [==============================] - 12s - loss: 148.5167 - mean_squared_error: 0.0403
Epoch 62/100
60000/60000 [==============================] - 12s - loss: 148.4498 - mean_squared_error: 0.0402
Epoch 63/100
60000/60000 [==============================] - 12s - loss: 148.3782 - mean_squared_error: 0.0402
Epoch 64/100
60000/60000 [==============================] - 12s - loss: 148.3564 - mean_squared_error: 0.0402
Epoch 65/100
60000/60000 [==============================] - 12s - loss: 148.2764 - mean_squared_error: 0.0401
Epoch 66/100
60000/60000 [==============================] - 12s - loss: 148.2129 - mean_squared_error: 0.0401
Epoch 67/100
60000/60000 [==============================] - 12s - loss: 148.1271 - mean_squared_error: 0.0401
Epoch 68/100
60000/60000 [==============================] - 12s - loss: 148.1235 - mean_squared_error: 0.0401
Epoch 69/100
60000/60000 [==============================] - 12s - loss: 148.0465 - mean_squared_error: 0.0400
Epoch 70/100
60000/60000 [==============================] - 12s - loss: 148.0112 - mean_squared_error: 0.0400
Epoch 71/100
60000/60000 [==============================] - 12s - loss: 147.9145 - mean_squared_error: 0.0400
Epoch 72/100
60000/60000 [==============================] - 12s - loss: 147.8853 - mean_squared_error: 0.0399
Epoch 73/100
60000/60000 [==============================] - 12s - loss: 147.8278 - mean_squared_error: 0.0399
Epoch 74/100
60000/60000 [==============================] - 12s - loss: 147.7964 - mean_squared_error: 0.0399
Epoch 75/100
60000/60000 [==============================] - 12s - loss: 147.7580 - mean_squared_error: 0.0399
Epoch 76/100
60000/60000 [==============================] - 12s - loss: 147.6748 - mean_squared_error: 0.0398
Epoch 77/100
60000/60000 [==============================] - 12s - loss: 147.6575 - mean_squared_error: 0.0398
Epoch 78/100
60000/60000 [==============================] - 12s - loss: 147.5867 - mean_squared_error: 0.0398
Epoch 79/100
60000/60000 [==============================] - 12s - loss: 147.5454 - mean_squared_error: 0.0398
Epoch 80/100
60000/60000 [==============================] - 12s - loss: 147.5190 - mean_squared_error: 0.0398
Epoch 81/100
60000/60000 [==============================] - 12s - loss: 147.4637 - mean_squared_error: 0.0397
Epoch 82/100
60000/60000 [==============================] - 12s - loss: 147.4142 - mean_squared_error: 0.0397
Epoch 83/100
60000/60000 [==============================] - 12s - loss: 147.3433 - mean_squared_error: 0.0397
Epoch 84/100
60000/60000 [==============================] - 12s - loss: 147.3191 - mean_squared_error: 0.0397
Epoch 85/100
60000/60000 [==============================] - 12s - loss: 147.3064 - mean_squared_error: 0.0396
Epoch 86/100
60000/60000 [==============================] - 12s - loss: 147.2359 - mean_squared_error: 0.0396
Epoch 87/100
60000/60000 [==============================] - 12s - loss: 147.2098 - mean_squared_error: 0.0396
Epoch 88/100
60000/60000 [==============================] - 12s - loss: 147.1685 - mean_squared_error: 0.0396
Epoch 89/100
60000/60000 [==============================] - 12s - loss: 147.0960 - mean_squared_error: 0.0395
Epoch 90/100
60000/60000 [==============================] - 12s - loss: 147.0898 - mean_squared_error: 0.0395
Epoch 91/100
60000/60000 [==============================] - 12s - loss: 147.0344 - mean_squared_error: 0.0395
Epoch 92/100
60000/60000 [==============================] - 12s - loss: 146.9816 - mean_squared_error: 0.0395
Epoch 93/100
60000/60000 [==============================] - 12s - loss: 146.9709 - mean_squared_error: 0.0395
Epoch 94/100
60000/60000 [==============================] - 12s - loss: 146.9162 - mean_squared_error: 0.0394
Epoch 95/100
60000/60000 [==============================] - 12s - loss: 146.8808 - mean_squared_error: 0.0394
Epoch 96/100
60000/60000 [==============================] - 14s - loss: 146.8675 - mean_squared_error: 0.0394
Epoch 97/100
60000/60000 [==============================] - 14s - loss: 146.7880 - mean_squared_error: 0.0394
Epoch 98/100
60000/60000 [==============================] - 13s - loss: 146.7733 - mean_squared_error: 0.0394
Epoch 99/100
60000/60000 [==============================] - 14s - loss: 146.7276 - mean_squared_error: 0.0394
Epoch 100/100
60000/60000 [==============================] - 13s - loss: 146.7409 - mean_squared_error: 0.0394
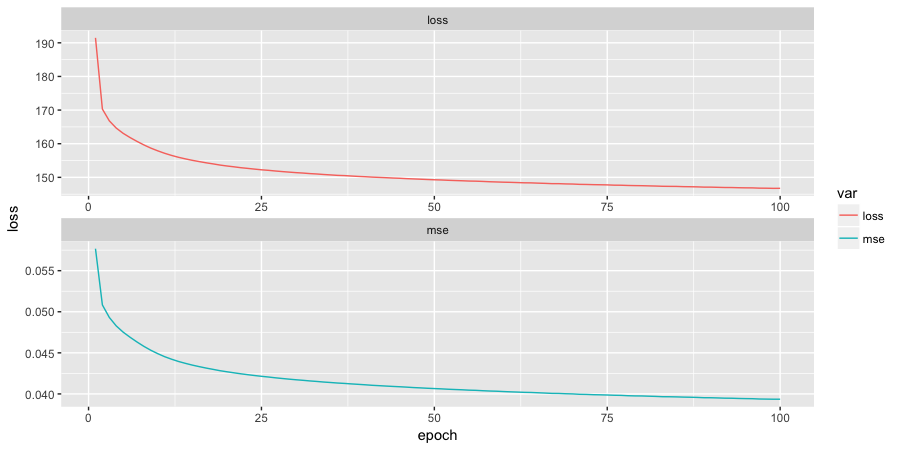
# MSEとLossの経過をプロット
> dplyr::data_frame(
mse = unlist(vae_hist$history$mse),
loss = unlist(vae_hist$history$loss)
) %>%
tibble::rownames_to_column(var = "epoch") %>%
dplyr::mutate(epoch = as.integer(x = epoch)) %>%
tidyr::gather(key = var, value = loss, -epoch) %>%
ggplot2::ggplot(data = ., mapping = ggplot2::aes(x = epoch, y = loss, group = var, colour = var)) +
ggplot2::geom_line() +
ggplot2::facet_wrap(facets = ~ var, nrow = 2, scales = "free")
わりと収束していそうですが、もう少しEpochを回してもよさそうですね。
Tensorboard
学習時のコールバックにTensorboardオブジェクトを加えていたので、ターミナルから起動することでTensorboardによる学習経過の可視化できます。
# tensorboardコマンドがインストールされていれば下記でOK
$ tensorboard --logdir=~/tensor_board/
# 自前のMac環境ではインストールされていなかったので、下記のようにtensorboard.pyのスクリプトを叩いている
$ python /usr/local/lib/python2.7/site-packages/tensorflow/tensorboard/tensorboard.py --logdir=~/tensor_board/
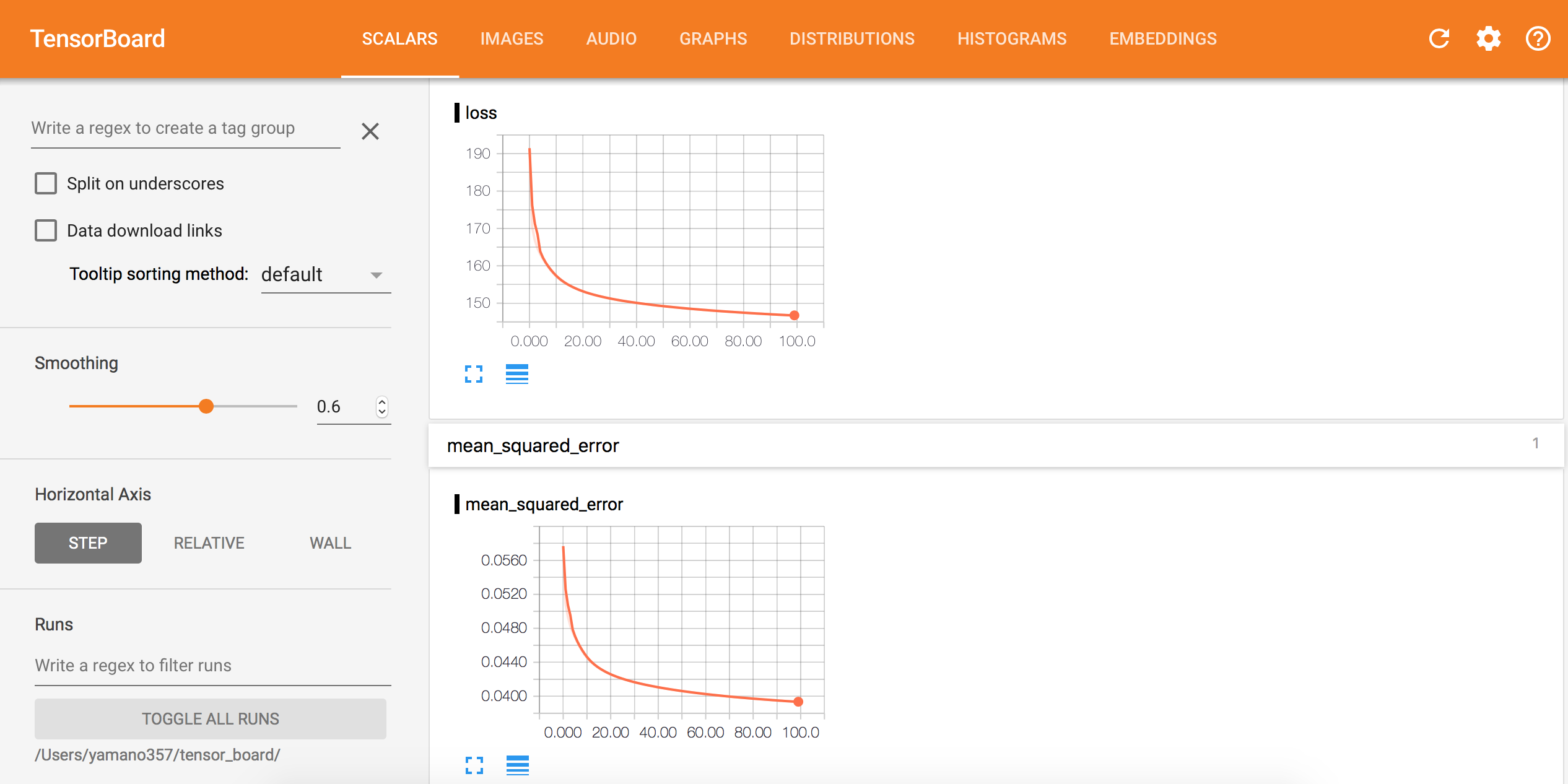
Tensorboardの起動後は「http://localhost:6006」(EC2上で起動している場合はlocalhostではなくインスタンスIPで確認可能。ただし、セキュリティグループのルールで6006が空いていること)にアクセスすることで、下記のような画面で学習状況を確認できます。
Encorder
encoder <- keras$models$Model(input = x, output = z_mean)
x_test_encoded <- encoder$predict(x = x_test, batch_size = BATCH_SIZE)
# encorderのモデルの要約出力
> encoder$summary()
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_1 (InputLayer) (100, 784) 0
____________________________________________________________________________________________________
dense_1 (Dense) (100, 256) 200960 input_1[0][0]
____________________________________________________________________________________________________
dense_2 (Dense) (100, 2) 514 dense_1[0][0]
====================================================================================================
Total params: 201,474
Trainable params: 201,474
Non-trainable params: 0
____________________________________________________________________________________________________
# encorderのモデル構成を可視化
> DiagrammeR::grViz(diagram = model_dot(model = encoder, show_shapes = TRUE)$create(prog = "dot", format = "dot"))

Generator
decoder_input <- keras$layers$Input(shape = list(LATENT_DIM))
h_decoded_ <- decoder_h$`__call__`(decoder_input)
x_decoded_mean_ <- decoder_mean$`__call__`(h_decoded_)
generator <- keras$models$Model(input = decoder_input, output = x_decoded_mean_)
# generatorのモデルの要約出力
> generator$summary()
Layer (type) Output Shape Param # Connected to
====================================================================================================
input_2 (InputLayer) (None, 2) 0
____________________________________________________________________________________________________
dense_4 (Dense) multiple 768 input_2[0][0]
____________________________________________________________________________________________________
dense_5 (Dense) multiple 201488 dense_4[1][0]
====================================================================================================
Total params: 202,256
Trainable params: 202,256
Non-trainable params: 0
____________________________________________________________________________________________________
# generatorのモデル構成を可視化
> DiagrammeR::grViz(diagram = model_dot(model = generator, show_shapes = TRUE)$create(prog = "dot", format = "dot"))

画像生成部
generatorに乱数値を与え、数値画像を表す行列を生成します。
# 生成用環境の設定
n <- 15
digit_size <- 28
grid_x <- qnorm(p = seq(from = 0.05, to = 0.95, length.out = n), mean = 0, sd = 1)
grid_y <- qnorm(p = seq(from = 0.05, to = 0.95, length.out = n), mean = 0, sd = 1)
# Pythonのビルトイン関数を使うためにreticulate::import_builtinsを利用
m <- reticulate::import_builtins(convert = TRUE)
# 下記のようにしてPythonの関数を使うことも可能
ii <- reticulate::iterate(x = m$enumerate(grid_x))
jj <- reticulate::iterate(x = m$enumerate(grid_x))
pl <- apply(
X = expand.grid(sapply(X = ii, FUN = "[[", 2), sapply(X = jj, FUN = "[[", 2)),
MARGIN = 1,
FUN = function(ii) {
# 乱数から画像生成
x_decoded <- generator$predict(x = matrix(data = ii, nrow = 1, ncol = 2))
return(
grid::rasterGrob(
image = matrix(data = x_decoded[1, ], nrow = digit_size, ncol = digit_size, byrow = FALSE),
interpolate = FALSE
)
)
}
)
ml <- gridExtra::marrangeGrob(grobs = pl, nrow = n, ncol = n)
# ggplot2::ggsave(filename = "vae.png", plot = ml, device = "png")
数字画像が生成できるようになっていそうです。
まとめ
Pythonの関数定義を一部利用しましたが、VAEによる数字画像生成のexampleスクリプトを書き換え、R上で画像生成できるまで確認しました。Kerasのお勉強が進んだことにより、以前に行った短歌生成のクオリティを上げられるかもしれません。
また、当初はDCGANを試してみようとしたのですが、パラメータチューニングが厳しい点とKerasのexampleが怪しそうだったので諦めました(何度試してもうまくいかなかった)。
生成モデルのアプローチは応用の幅がありそうなので、もう少し詳しく触ってみようと思います。
参考
- 論文紹介 Semi-supervised Learning with Deep Generative Models
- 猫でも分かるVariational AutoEncoder
- KerasでVariational AutoEncoder
- Variational Autoencoder(VAE)で生成モデル
- VAEからCVAE with keras
- Variational Auto Encoder
- VAEとGANを活用したファッションアイテム検索システム
- Kerasで学ぶAutoencoder
- Keras Generative Adversarial Networks
- KerasでDCGAN書く
- はじめてのGAN
- MNIST Generative Adversarial Model in Keras
- Unrolled Generative Adversarial Networks [arXiv:1611.02163]
- Trainable = False isn't freezing weights
- Python object instantiation fails for classes defined in an R session
- Trying to use scikit-learn from R
実行環境
> devtools::session_info()
Session info ----------------------------------------------------------------------------------------------------
setting value
version R version 3.3.2 (2016-10-31)
system x86_64, darwin15.6.0
ui RStudio (1.0.136)
language (EN)
collate ja_JP.UTF-8
tz Asia/Tokyo
date 2017-02-26
Packages --------------------------------------------------------------------------------------------------------
package * version date source
assertthat 0.1 2013-12-06 CRAN (R 3.3.2)
colorspace 1.3-2 2016-12-14 CRAN (R 3.3.2)
DBI 0.5-1 2016-09-10 CRAN (R 3.3.2)
devtools 1.12.0 2016-12-05 CRAN (R 3.3.2)
DiagrammeR * 0.8.4 2016-07-17 CRAN (R 3.3.2)
digest 0.6.10 2016-08-02 CRAN (R 3.3.2)
dplyr * 0.5.0 2016-06-24 CRAN (R 3.3.2)
ggplot2 * 2.2.0 2016-11-11 CRAN (R 3.3.2)
gridExtra 2.2.1 2016-02-29 CRAN (R 3.3.2)
gtable 0.2.0 2016-02-26 CRAN (R 3.3.2)
htmltools 0.3.5 2016-03-21 CRAN (R 3.3.2)
htmlwidgets 0.8 2016-11-09 CRAN (R 3.3.2)
igraph 1.0.1 2015-06-26 CRAN (R 3.3.2)
influenceR 0.1.0 2015-09-03 cran (@0.1.0)
jsonlite 1.1 2016-09-14 CRAN (R 3.3.2)
labeling 0.3 2014-08-23 CRAN (R 3.3.2)
lazyeval 0.2.0 2016-06-12 CRAN (R 3.3.2)
magrittr 1.5 2014-11-22 CRAN (R 3.3.2)
memoise 1.0.0 2016-01-29 CRAN (R 3.3.2)
munsell 0.4.3 2016-02-13 CRAN (R 3.3.2)
plyr 1.8.4 2016-06-08 CRAN (R 3.3.2)
purrr * 0.2.2 2016-06-18 CRAN (R 3.3.2)
R6 2.2.0 2016-10-05 CRAN (R 3.3.2)
Rcpp 0.12.8 2016-11-17 CRAN (R 3.3.2)
readr * 1.0.0 2016-08-03 CRAN (R 3.3.2)
reticulate * 0.6.0 2017-02-17 Github (rstudio/reticulate@519fa07)
RevoUtils 10.0.2 2016-11-22 local
rstudioapi 0.6 2016-06-27 CRAN (R 3.3.2)
scales 0.4.1 2016-11-09 CRAN (R 3.3.2)
stringi 1.1.2 2016-10-01 CRAN (R 3.3.2)
stringr 1.1.0 2016-08-19 CRAN (R 3.3.2)
tibble * 1.2 2016-08-26 CRAN (R 3.3.2)
tidyr * 0.6.0 2016-08-12 CRAN (R 3.3.2)
tidyverse * 1.0.0 2016-09-09 CRAN (R 3.3.2)
visNetwork 1.0.2 2016-10-05 CRAN (R 3.3.2)
withr 1.0.2 2016-06-20 CRAN (R 3.3.2)
yaml 2.1.14 2016-11-12 CRAN (R 3.3.2)
$ python --version
Python 2.7.12
$ pip list --format=columns | grep -e "tensorflow" -e "Keras"
Keras 1.2.2
tensorflow 1.0.0