マイクラEEで円の描画を高速化してみる

はじめに（前回のおさらいと今回の取り組み）

　前回の記事では、マインクラフト Education Editionのコードビルダー（MakeCode）を使って、オーバーワールドに円を描くプログラムを作り、円周率を計算してみました。プログラム自体はロジックの簡便さを優先し、描きたい円を含む正方形のエリアをくまなく探索し、中心からの距離が半径$r$以下になるエリアを見つけるという方法を採用していましたが、この方法では、$r^2$のオーダーで計算量が増えていってしまいます。マイクラEE上では、もろもろの理由から、$r=128$が今回の描画上の限界でしたが、より大きな$r$に対してシミュレーションを行おうとする時に、この計算量の増え方は問題となります。そこで、この記事ではより効率的（高速）に円を描画するためのプログラムの改良を行います。結論としてはロジックの改良により$r^2$ではなく$r$に比例する程度の計算量で円を描画できるようにしていきます。
　なお、今回掲載するロジックと同様のものは、前回の記事へのコメントとして、fujitanozomuさんがすでに実装例を挙げてくださっており、より大きなrへの適用結果として適用限界の分析まで含めて投稿いただいております。fujitanozomuさんありがとうございます。
　今回の記事では、ロジックの改良で実際にどれくらい早くなるのかという点に着目して、マイクラの動画とPowerShellでの実行時間比較をご紹介したいと思います。

ロジックの改良

　これまでロジックで、計算量が$r^2$のオーダーで増加していってしまうのは、探索範囲となる正方形の領域をくまなく探索しているためです。$xz$平面上の、点$(x_c,z_c)$を中心とする半径$r$の円を表す二次曲線の方程式、$ (x-x_c)^2 + (z-z_c)^2 =r^2$をうまく用いることで、$x$軸方向の探索だけで、円の範囲を求められるようにロジックを改良します。円の中心が原点となるように座標変換を行うことで、方程式は$ x^2 + z^2 =r^2$のように簡便化できるので、以後はこちらの形式で問題を取り扱うことにします

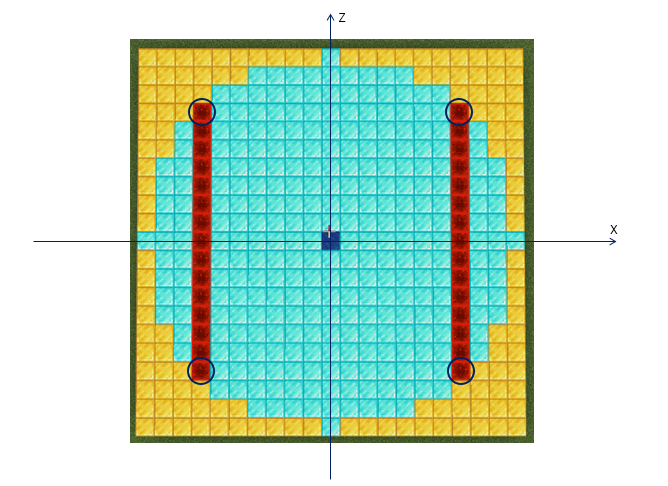
$x$軸方向の座標$x_1$における円周の座標を$(x_1,z_1)$とするとき、円の方程式から$z_1$は、$z_1 = \pm \sqrt{r^2-x_1^2} $ となり、$\sqrt{r^2-x_1^2}$から$-\sqrt{r^2-x_1^2}$までの範囲が円の内側となります。また、円は$z$軸に対する反転($x$を$-x$に置き換える変換)に対しても対象性があるので、$-x_1$においても同様のことがいえます。次の図は半径10の円を描いたものですが、$x=\pm 7$において、この方法で特定される円周の位置を4か所の青丸、円の内側の領域を赤（レッドストーンブロック）で示しています。円の内側に相当する領域を特定することができれば、1ブロックずつ中心からの距離を判定しブロックを置いていくのではなく、範囲指定でブロックを埋めていくことが可能となります。

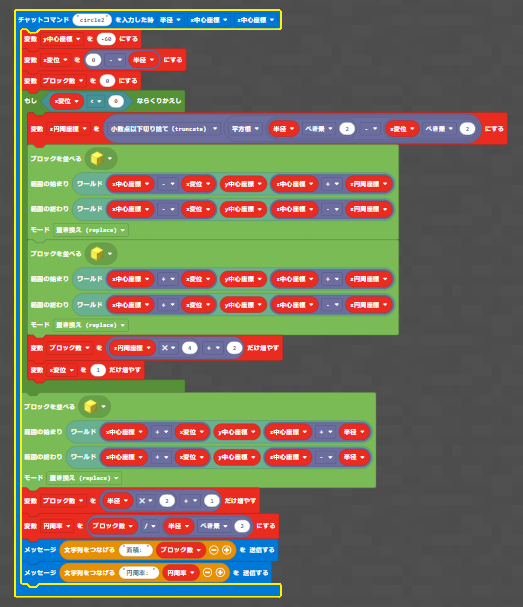
ここまでに述べた方法を持ちいて、円の内側に当たる領域を特定し、円を描くようにしたプログラムが図Xです。前回のプログラムと比べて繰り返しのループが$x$についてのみになっており、計算量が少なくなっています。

let y中心座標 = 0
let x変位 = 0
let ブロック数 = 0
let z円周座標 = 0
let 円周率 = 0
let x開始座標 = 0
let z開始座標 = 0
let z変位 = 0
let 距離の二乗 = 0
player.onChat("circle2", function (半径, x中心座標, z中心座標) {
    y中心座標 = -60
    x変位 = 0 - 半径
    ブロック数 = 0
    while (x変位 < 0) {
        z円周座標 = Math.trunc(Math.sqrt(半径 ** 2 - x変位 ** 2))
        blocks.fill(
        GOLD_BLOCK,
        world(x中心座標 - x変位, y中心座標, z中心座標 + z円周座標),
        world(x中心座標 - x変位, y中心座標, z中心座標 - z円周座標),
        FillOperation.Replace
        )
        blocks.fill(
        GOLD_BLOCK,
        world(x中心座標 + x変位, y中心座標, z中心座標 + z円周座標),
        world(x中心座標 + x変位, y中心座標, z中心座標 - z円周座標),
        FillOperation.Replace
        )
        ブロック数 += z円周座標 * 4 + 2
        x変位 += 1
    }
    blocks.fill(
    GOLD_BLOCK,
    world(x中心座標 + x変位, y中心座標, z中心座標 + 半径),
    world(x中心座標 + x変位, y中心座標, z中心座標 - 半径),
    FillOperation.Replace
    )
    ブロック数 += 半径 * 2 + 1
    円周率 = ブロック数 / 半径 ** 2
    player.say("面積：" + ブロック数)
    player.say("円周率：" + 円周率)
})

実演

　それでは実際に、どれだけ円の描画が早くなったのかを動画で実演します。動画では、最初に前回のプログラムを使って円を描いた後、今回改良したプログラムを使って違う色の円に書き換えています。描画される円が同じであることと、改良版のプログラムでの描画が高速化されていることを確認できると思います。

rの増加に対する実行時間の比較（PowerShell）

　前節では、ロジックの違いによる実行時間の差異をマイクラの動画としてご確認いただきましたが、もう少し定量的に測定した結果をご紹介します。改良前のロジックをPowerShellで実装したものがcircle1.ps1、改良後のロジックを実装したものがcircle2.ps1です。

circle1.ps1

Param(
   [long]$r = $Args[0],
   [long]$blockcount = 0,
   [long]$xcount = -$r,
   [long]$zcount = -$r,
   [long]$distance =0
   )

$now = Get-Date
$start_log = ("{0:yyyy/MM/dd HH:mm:ss.ffff} {1}" -f $now, $_)
Write-Host $start_log
while($xcount -le $r){
   while($zcount -le $r){
       $distance = $xcount*$xcount + $zcount*$zcount
       if($distance -le $r*$r){
           $blockcount++
       }
       $zcount++
   }   
   $xcount++
   $zcount = -$r
}
$pi = $blockcount/$r/$r
$now = Get-Date
$end_log = ("{0:yyyy/MM/dd HH:mm:ss.ffff} {1}" -f $now, $_)
Write-Host $end_log
Write-Host $r,$blockcount,$pi

Param(
   [long]$r = $Args[0],
   [long]$blockcount = 0,
   [long]$xcount = -$r,
   [long]$zcount = 0
   )

$now = Get-Date
$start_log = ("{0:yyyy/MM/dd HH:mm:ss.ffff} {1}" -f $now, $_)
Write-Host $start_log
while($xcount -lt 0){
   $zcount = [Math]::Truncate([Math]::Sqrt($r*$r - $xcount*$xcount)) 
   $blockcount = $blockcount + $zcount*4 + 2 
   $xcount++
}
$blockcount = $blockcount + $r*2 + 1
$pi = $blockcount/$r/$r
$now = Get-Date
$end_log = ("{0:yyyy/MM/dd HH:mm:ss.ffff} {1}" -f $now, $_)
Write-Host $end_log
Write-Host $r,$blockcount,$pi

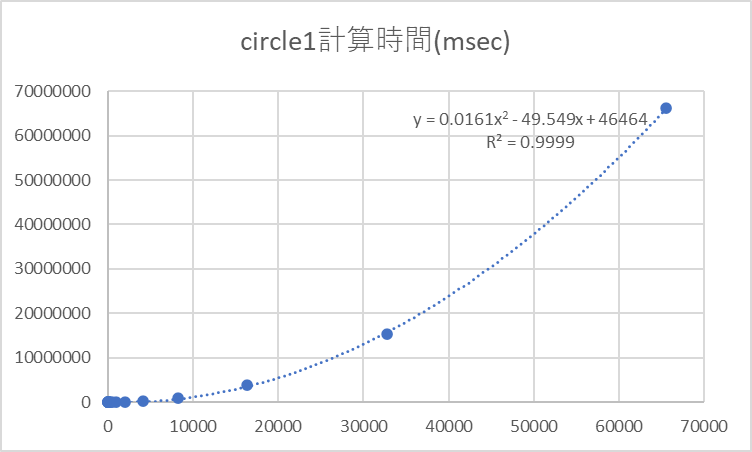
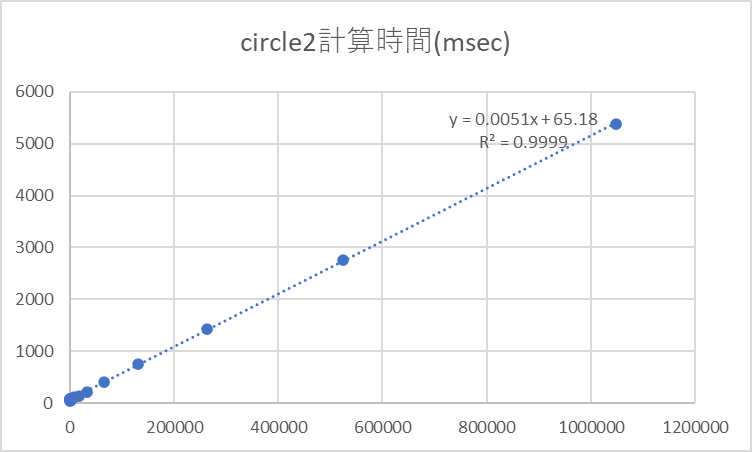
それぞれのプログラムで半径を大きくしていった時の計算時間をまとめたものが以下の表となります。計算時間の単位はミリ秒で、数値は5回の実行結果の平均値です。$r=32$あたりから、circle1の計算時間がcircle2と比べて急激に増大する傾向が見て取れると思います。$r=131072$以降の半径に対しては、circle1は計算時間がかかりすぎて、本稿の投稿までには測定不能でした。

r	circle1.ps1	circle2.ps1
1	33.6	37.8
2	72.2	71.6
4	68.2	60.2
8	73.4	64
16	78.2	73.2
32	86.8	61
64	138.2	58.6
128	317.2	77.6
256	1049.4	79.8
512	3900.8	68.8
1024	15330.6	64
2048	60373.6	62.8
4096	242002.8	82.2
8192	962802	109.4
16384	3840905	143.2
32786	15391490.8	220.4
65536	66127313	408
131072	-	742.2
262144	-	1422.2
524288	-	2748
1048576	-	5388.4

$r$を横軸、計算時間を縦軸にプロットすると、circle1が$r^2$、circle2が$r$に比例して増大することがわかります。

まとめ

今回の記事のまとめです。

• Advent Calendar 12/1の記事のロジックをより少ない計算時間で実行できるように改良しました。
• 改良結果をマイクラ上の円の描画時間で比較できるよう動画にしました。
• 改良前後のプログラムが、それぞれ$O(r^2)$と$O(r)$で増大することを、Powershellでの実行結果から確認しました。