株式会社サイシードのインターンシップとしてUnity上で自走式ロボットアームを作成しました。ここでは、そのロボットアームをどのように作成したかを書きます。
やったこと
下の動画が完成したアームです。積み上がったキューブをハノイの塔のルールに従って移動させているのが分かるかと思います。さらに、キューブを置く位置を初めに変更できる機能もあります。

今後
今回はUnity上の仮想的なロボットアームでしたが、次のようなロボットアームを用いると十分実現可能のように考えられます。今後はこういったハードウェアに当記事のような技術を適用していきたいと考えています。

※Physical Computing Lab の「DOBOT Magician」のページ
https://www.physical-computing.jp/page/14
作成手順
なかなか複雑なので、以下のように手順を分けて説明します。
- ハノイの塔の解き方について
- キューブを取るためのアームの角度計算
- 「掴む」「放す」について
- 「移動」について
- 状態の管理
1. ハノイの塔の解き方について
情報系の方々ではよく扱われる問題のようですね。
アルゴリズムについてはこちらのページに詳しく記述されており、参考にしました。
今回はアームを使ってキューブを移動させるため、予めハノイの塔を解いた時に移動させる順番を記録しておき、あとで5.に示すフローチャートのループごとに、ひとつずつターゲットとなるキューブをゴールとなる塔へ移動させます。
つまり始めに動かすべきキューブの順序を決定しておき、あとはそれに従いアームを動作させます。
2. キューブを取るためのアームの計算角度
アームを動かすために、各アームの角度計算をしなければなりません。
ターゲットとなるキューブの座標やアーム自身の座標から(逆)三角関数を解いて角度を求めていきます。
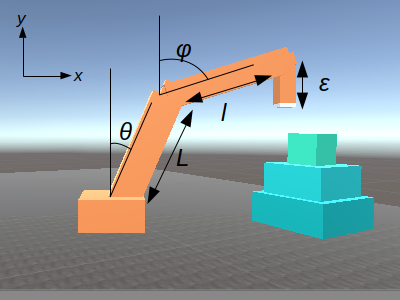
上図に示すように、角度$\theta, \phi$とおきます。また、アームを構成する3つの腕の長さを根元に近い方からそれぞれ$L, l, \epsilon$と設定します。
いま、アームが動く図にある平面内において、ターゲットとなるキューブの座標を$(x, y)$とおきます。この場合次の2式が成立します。
\begin{align}
x &= L\sin\theta + l \sin \phi\\
y &= L\cos\theta + l\cos\phi - \epsilon
\end{align}
ここで、
\begin{align}
\beta &=\cos^{-1}(\frac{x^2+(y+\epsilon)^2-l^2-L^2}{2lL})\\A&=\sqrt{(\frac{x^2+(y+\epsilon)^2-L^2+l^2}{2l})^2+L^2\sin^2\beta}
\end{align}
とおく。$\phi, \theta$について解くと、
\begin{align}
\phi &= \tan^{-1}\left(\frac{x}{A}\right)-\tan^{-1}\left(\frac{2lL\sin\beta}{r^2+(y+\epsilon)^2}\right)\\
\theta &= \phi+\beta
\end{align}
と表すことができます。
3. 「掴む」「放す」について
実際に掴んだり離したりなど主要な動作についてです。これらを表現するために、以下のような処理をするスクリプトをアームにアタッチしています。
アームの角度
いま、「2.キューブを取るためのアームの角度計算」における長さが$L$のアームをアーム1、$l$のアームをアーム2とします。2つのアームにはそれぞれ別のスクリプトをアタッチさせます。
ここで$x$には$\theta$または$\phi$を次のように代入します。
if (x - theta < -0.5) {
x += 0.5f;
}
else {
//this.GetComponent<RotationConstraint>().enabled = true;
//のようにして、Constraintを有効にする
}
if文の条件であるx-theta<-0.5がfalseになったときにPosition Constraint(後述)が有効になるようにあらかじめ設計しておくと、キューブを掴むことができます。掴んだ後、先ほどとは逆にx -= 0.5fのようにしてxに値を代入し直して持ち上げることができます。
Update()内で次のようにして角度を更新します。これにより角度xが反映されます。
transform.rotation = Quaternion.Euler((int)x, 0, 0);
※xをfloat型で代入すると小数の桁のせいで震えが生じる為、わざとint型で代入しています。
掴む
先に述べましたが、__結論から言うとUnityのConstraintというコンポーネントが便利です。__PositionやRotationなどを指定したオブジェクトとリンクさせることができます。ここではターゲットのキューブにPosition Constraintをアタッチし、アームの先が十分近づいたときにPosition Constraintが有効になるようにしました。これにより「掴む」を表現できます。Constraintについてはこちらのページを参考にしました。
放す
「放す」ときも同じで、Position Constraintを無効にすれば放すことができます。
アームの角度について、掴むときは__2.__の$x$, $y$をターゲットとなるキューブの座標として$\theta$, $\phi$を求めました。放す際はこれと同様にして__2.__の$x$, $y$にゴールとなる塔の座標を入れ、$\theta$, $\phi$を求めます。
4. 「移動」について
ターゲットとなるキューブ、またはゴールとなる塔が、アーム自身と離れていた場合はアーム自体が移動する必要があります。
アームの土台回転
ターゲットに向けてアームを回転させます。
まずコードを以下に示します。
void Catch() {
floor_rot = Mathf.Atan2(x_relative, z_relative) * Mathf.Rad2Deg;
if (y - floor_rot < 180 && y - floor_rot > 0) {
y -= 1.5f;
}
else if (y - floor_rot > -360 && y - floor_rot <= -180) {
y -= 1.5f;
}
else if (y - floor_rot >= 360) {
y -= 1.5f;
}
else if (y - floor_rot <= -360) {
y += 1.5f;
}
else if (y - floor_rot < 0 && y - floor_rot >= -180) {
y += 1.5f;
}
else if (y - floor_rot < 360 && y - floor_rot >= 180) {
y += 1.5f;
}
else {
y += 1.5f;
}
}
上のようなCatch()関数をメインループUpdata()内で呼び出すことによりアームを旋回させます。キューブの位置によって、最短での回転方向が右回りか左回りに決まります。このため、回転の方向が変わるように条件を細かに分けます。このとき、条件の境界に空白が生まれないように注意します。ただし、x_relative, z_relativeは相対的なキューブの位置です(後述)。
土台の移動
いま、取りたいキューブの座標とキューブを持っていきたい塔(ゴール)のアームからみたときの相対的な座標を
x_relative = target_pos_x - transform.position.x;
y_relative = target_pos_y - transform.position.y;
z_relative = target_pos_z - transform.position.z;
x_goal_relative = goal_script.pos_x - transform.position.x;
y_goal_relative = goal_script.pos_y - transform.position.y + adjust;
z_goal_relative = goal_script.pos_z - transform.position.z;
とします。transform.position.xなどはアーム自身の座標です。target_pos_xなどはキューブの座標です。ここでadjustはキューブを積むときの置く高さです。既にキューブがおいてあれば、その分高く積む必要があります。そこで下のHeight()で高さを決定しました。
void Height() {
adjust = 0;
if (target[work_times + 1] != 0 && Mathf.Abs(goal_script.pos_z - target_script.pos_z) < 2f) {
adjust += 2.0f;
}
if (target[work_times + 1] != 1 && Mathf.Abs(goal_script.pos_z - target_script.pos_z) < 2f) {
adjust += 2.0f;
}
if (target[work_times + 1] != 2 && Mathf.Abs(goal_script.pos_z - target_script.pos_z) < 2f) {
adjust += 2.0f;
}
}
といったようにキューブの数だけ置くべき高さを調整(adjust)しましょう。
ハノイの塔をあらかじめ解いてあるので、いまキューブがどこにあるかはわかると思います。if文の条件はこれらから見積もります。
求めた相対的な座標から以下のように実際に移動します。
void Move() {
Vector3 pos = transform.position;
velocity_x = 0.2f * Mathf.Abs(x_relative) / Mathf.Sqrt(x_relative * x_relative + z_relative * z_relative);
velocity_z = 0.2f * Mathf.Abs(z_relative) / Mathf.Sqrt(x_relative * x_relative + z_relative * z_relative);
if (x_relative > 0) {
pos.x += velocity_x;
}
else if (x_relative < 0) {
pos.x -= velocity_x;
}
if (z_relative > 0) {
pos.z += velocity_z;
}
else if (z_relative < 0) {
pos.z -= velocity_z;
}
transform.position = pos;
}
ここでvelocity_x, velocity_zは移動速度です。取りたいキューブにまっすぐ進んでいくようにノルムをとって割っています。
下部のif文でvelocity_x, velocity_zをアームの座標であるpos.x, pos.zに足し合わせて移動します。
キューブを取った後の塔(ゴール)への移動も同様です。x_relative, z_relativeをそれぞれx_goal_relative, z_goal_relativeに置換するだけで大丈夫です。
5.状態の管理
動作の流れ
1〜4で各動作について説明しました。これらは、次のようなフローで動作します。
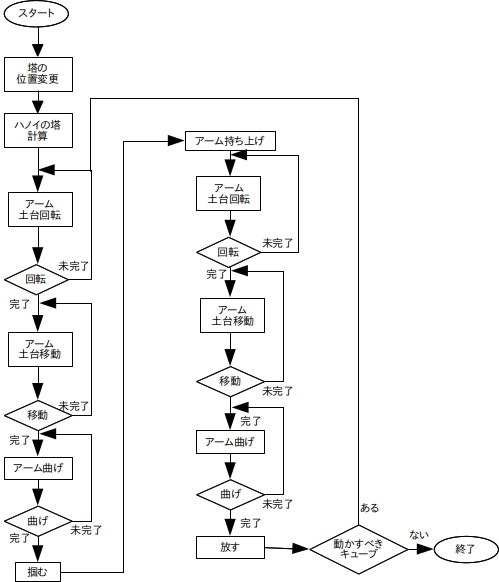
図のダイヤ型の判断部分ではbool型の変数をおいて、動作が完了していればtrueにする、といったような処理を行いました。次にその例を示します。
if (catch_state == false && Floor_script.floor_state == true && Floor_script.move1_state == true) {
Catch();
}
これらのフローはUpdate()内部においた関数を毎ループ呼び出すことにより動作しています。関数を実行するかどうかは上のようなbool型などの変数で状態管理を行っています。つまり、グラフィックのクオリティに動作速度が依存します。ビルドしたファイルを低質の画質で実行した場合、早回しのようになることに注意されたいです。
実行前のアクション
先に述べました通り、ロボットアームの動作実行前に、今回はゴールとなる3つの塔の位置をスライダーでそれぞれ自由に移動させることができます。これは毎ループ、ターゲットとなるキューブとゴールとなる塔の座標を参照しているためです。

UIについて、特にスライダーの使い方はこちらを参考にいたしました。
まとめ
今回のために作成したC#スクリプトはすべてgithubに上げておきました。
今回はUnityを用いました。Unityを使う場合はモデルを作るところが難関だと感じました。また、複数のコンポーネントを複雑に作動(例えば、HingeJointをアタッチしたオブジェクトにさらにHingeJointをアタッチしたオブジェクトをつける)させると、想定した動きをしないことがあります。
以上では自走式ロボットアームの制作を行いました。お読みいただきありがとうございました。