光量子計算ライブラリ Strawberry Fields を用いた量子ニューラルネットワークの簡単な例の解説

はじめに

近年、量子コンピューティングの分野では、量子ニューラルネットワーク（QNN）の研究が盛んに行われています。今回は、光量子計算ライブラリ Strawberry Fields という光量子コンピュータのライブラリから、QNNの基本的な構造と最適化プロセスが紹介されている、

の記事になるべく即して、解説したいと思います。

にこの記事の実行結果があります。

Strawberry Fields とは？

Strawberry Fields は、光量子コンピューティングをシミュレートするためのPythonライブラリです。量子回路を構築し、量子状態のシミュレーションや量子ゲートの操作などを行うことができます。特に、連続変数量子情報（CV-QI）に焦点を当てた設計になっており、様々な量子状態の生成や操作が可能です。

まずは、Strawberry Fieldsをインストールする必要があります。通常、次のコマンドを使用します。

pip install strawberryfields

Blackbird とは？

Blackbird は、XanaduのStrawberry Fields用に設計された量子プログラミング言語で、光量子コンピューター上での量子プログラムの記述に適しています。以下に、Blackbirdの基本文法について説明します。

具体的な量子操作（ゲートなど）は、量子モードに対して適用されます。以下の例では、| の右側が量子状態、左が作用させるゲートになります。

Sgate(alpha, 0) | 0  # モード0にスクイーズゲートを適用
BSgate(pi/4, pi) | (1, 2)  # モード1と2にビームスプリッターを適用
Rgate(delta) | 2  # モード2に回転ゲートを適用

量子力学における、状態ベクトルに左から演算子を作用させる、という直感に合致した記法を採用しています。

プログラムの概要

以下は、単一モードの量子ニューラルネットワークを構築し、特定の量子状態（単一光子状態）に対する最適化を行うプログラムの概要について説明します。

機械学習との関係

連続量子ニューラルネットワークのレイヤーは、下記のように定義されます。

\mathcal{L}:=\Phi \circ \mathcal{D} \circ \mathcal{U}_2 \circ \mathcal{S} \circ \mathcal{U}_1

ここで、

• $\mathcal{U}_k=U_k\left(\boldsymbol{\theta}_k, \phi_k\right)$ は $N$ モードの干渉計( interferometer 関数で実現)
• $\mathcal{D}=\otimes_{i=1}^N D\left(\alpha_i\right)$ はシングルモードの displacement ゲート (Dgate) で、複素変位量 $\alpha_i \in \mathbb{C}$ の関数
• $\mathcal{S}=\otimes_{i=1}^N S\left(r_i\right)$ は、シングルモードのスクイーズドゲード (Sgate) で、それぞれのモードが squeezing parameter $r_i \in \mathbb{R}$ の関数
• $\Phi=\otimes_{i=1}^N \Phi\left(\lambda_i\right)$ が非ガウスゲートで、パラメータ $\lambda_i \in \mathbb{R}$ の関数

で定義されるものです。

インターフェロメーターの定義

インターフェロメーターは、光の経路を操作する装置です。ここでは、ビームスプリッター（光の分割・合流を行う装置）と位相シフター（光の位相を変更する装置）を組み合わせています。関数interferometerは、これらの要素をパラメータ化し、量子回路に適用します。

インターフェロメーター関数の詳細

インターフェロメーターは、光の経路を制御し、光子の状態を変化させるための量子回路です。

def interferometer(params, q):
    """Parameterised interferometer acting on ``N`` modes.
       Nモードに作用するパラメータ化されたインターフェロメーター。

    Args:
        params (list[float]): list of length ``max(1, N-1) + (N-1)*N`` parameters.
        ビームスプリッターの角度、位相、局所回転のパラメーターのリスト

            * The first ``N(N-1)/2`` parameters correspond to the beamsplitter angles
            * The second ``N(N-1)/2`` parameters correspond to the beamsplitter phases
            * The final ``N-1`` parameters correspond to local rotation on the first N-1 modes

        q (list[RegRef]): list of Strawberry Fields quantum registers the interferometer
            is to be applied to
       Strawberry Fieldsの量子レジスターのリスト

    """
    N = len(q)
    theta = params[: N * (N - 1) // 2]
    phi = params[N * (N - 1) // 2 : N * (N - 1)]
    rphi = params[-N + 1 :]

    if N == 1:
        # the interferometer is a single rotation
        ops.Rgate(rphi[0]) | q[0]
        return

    n = 0  # keep track of free parameters

    # Apply the rectangular beamsplitter array 長方形のビームスプリッター配列の適用
    # The array depth is N
    for l in range(N):
        for k, (q1, q2) in enumerate(zip(q[:-1], q[1:])):
            # skip even or odd pairs depending on layer
            if (l + k) % 2 != 1:
                ops.BSgate(theta[n], phi[n]) | (q1, q2)
                n += 1

    # apply the final local phase shifts to all modes except the last one
    # 最後のモードを除く全モードに局所位相シフトを適用
    for i in range(max(1, N - 1)):
        ops.Rgate(rphi[i]) | q[i]
    # Rgate only applied to first N - 1 modes

パラメータの分割

theta = params[: N * (N - 1) // 2]
phi = params[N * (N - 1) // 2 : N * (N - 1)]
rphi = params[-N + 1 :]

パラメータリスト paramsから、ビームスプリッターの角度（theta）、位相（phi）、および局所回転（rphi）のパラメーターを抽出します。

単一モードの場合

if N == 1:
    ops.Rgate(rphi[0]) | q[0]
    return

モードが1つの場合、インターフェロメーターは単一の回転として機能します。この場合、Rgateを適用して処理を終了します。

ビームスプリッター配列の適用

n = 0  # keep track of free parameters
for l in range(N):
    for k, (q1, q2) in enumerate(zip(q[:-1], q[1:])):
        if (l + k) % 2 != 1:
            ops.BSgate(theta[n], phi[n]) | (q1, q2)
            n += 1

nは使用されるパラメーターのインデックスを追跡します。全てのモードのペアに対してビームスプリッターを適用します。lとkはレイヤーとペアのインデックスを示し、奇数か偶数かによってペアをスキップします。

局所位相シフトの適用

for i in range(max(1, N - 1)):
    ops.Rgate(rphi[i]) | q[i]

最後のモードを除く全てのモードに局所位相シフトを適用します。これにより、各モードの位相が個別に調整されます。

量子ニューラルネットワークレイヤーの定義

量子ニューラルネットワーク（QNN）の各レイヤーでは、スクイーズゲート、変位ゲート、Kerrゲートなどを用いて量子状態に操作を加えます。関数layerはこれらのゲートを組み合わせ、量子レジスタ（量子ビット）に適用するためのパラメータを設定します。

量子ニューラルネットワークの詳細

def layer(params, q): 関数は、量子ニューラルネットワークの一層（レイヤー）を表しており、様々な量子ゲートを適用します。

def layer(params, q):
    N = len(q)
    M = int(N * (N - 1)) + max(1, N - 1)

    int1 = params[:M]
    s = params[M : M + N]
    int2 = params[M + N : 2 * M + N]
    dr = params[2 * M + N : 2 * M + 2 * N]
    dp = params[2 * M + 2 * N : 2 * M + 3 * N]
    k = params[2 * M + 3 * N : 2 * M + 4 * N]

    interferometer(int1, q)

    for i in range(N):
        ops.Sgate(s[i]) | q[i]

    interferometer(int2, q)

    for i in range(N):
        ops.Dgate(dr[i], dp[i]) | q[i]
        ops.Kgate(k[i]) | q[i]

(1) 変数の初期化

• N: 量子レジスタの数。
• M: 各インターフェロメーターに必要なパラメータの数。

(2) パラメータの分割

• int1, int2: 二つのインターフェロメーターに適用するパラメータ。
• s: スクイーズゲートに適用するパラメータ。
• dr, dp: 変位ゲートに適用する実数部と虚数部のパラメータ。
• k: Kerrゲートに適用するパラメータ。

(3) インターフェロメーターの適用

• interferometer(int1, q): 最初のインターフェロメーターを適用します。

(4) スクイーズゲートの適用

• ops.Sgate(s[i]) | q[i] 各量子レジスタにスクイーズゲートを適用します。スクイーズゲートは、量子状態の特定の次元を圧縮または拡張します。

(5) 第二のインターフェロメーターの適用:

• interferometer(int2, q): 第二のインターフェロメーターを適用します。

(6) 変位ゲートとKerrゲートの適用:

• ops.Dgate(dr[i], dp[i]) | q[i]: 各量子レジスタに変位ゲートを適用します。変位ゲートは、量子状態を特定の量だけ「移動」させます。
• ops.Kgate(k[i]) | q[i]: 各量子レジスタにKerrゲートを適用します。Kerrゲートは、非線形性を導入し、量子状態をより複雑にします。

この関数は、量子回路の各層を構築し、量子状態を操作するための一連のゲートを適用します。これらの操作は、量子コンピューターが特定のタスク状態の生成、パターン認識を行うための基礎的な部分になります。

要素数 N や M の意味の補足

def layer(params, q): 内で定義されている、

N = len(q)
M = int(N * (N - 1)) + max(1, N - 1)

で定義される、N と M について整理してみます。N は q という量子状態の配列(光量子の場合は、モードと呼ぶ)の数なので、モード数です。Mは少し複雑なので一つづつ考えます。

量子干渉計は、一連のビームスプリッターと位相シフターから構成され、複数の量子モード（この場合はNモード）に対して複雑な変換を施すことが目的です。

• ビームスプリッター: 任意の2つのモード間で光子の状態を分割・結合することができる要素です。Nモードのシステムでは、最大で N(N - 1) / 2 個 (つまり$_nC_2$)のビームスプリッターが必要になります。

• 位相シフター: 個々のモードに位相の変化を加える要素です。Nモードのシステムでは、最大で N - 1 個の位相シフターが必要になります。-1 がつくのは、位相は相対的なものなので、誰か一人は基準となるので、N-1人分だけでよいです。

Mの計算

• Mは、干渉計に必要なビームスプリッターと位相シフターの総数を表します。
• N * (N - 1): これは全てのモードのペアに対してビームスプリッターを配置するために必要な数です。しかし、実際には隣接するモード間のみにビームスプリッターを配置するため、この数は2で割られます。したがって、N * (N - 1) / 2がビームスプリッターの数になります。これが使われる場所は下記で、

def interferometer(params, q):
...
ops.BSgate(theta[n], phi[n]) | (q1, q2)

のように、ビームスプリッター ops.BSgate(theta[n], phi[n]) では、theta と phi の２つのパラメータが必要なので、N * (N - 1) / 2 x 2 = N * (N-1) 個のパラメータが必要です。

• max(1, N - 1): これは各モードに対して必要な位相シフターの数です。少なくとも1つの位相シフターが必要で、モードが1つのみの場合はそれ以上の位相シフターは必要ありません。

したがって、Mはこれらの要素の合計として int(N * (N - 1)) + max(1, N - 1)で計算されます。これにより、干渉計内の各要素に対してパラメータを適切に割り当てることができます。

Kerrゲートの補足

「Kerrゲート」は、光量子計算で重要な量子ゲートの一つです。このゲートは、Kerr効果（光の強度に依存して物質の屈折率が変化する現象）を利用して、光の量子状態に非線形変化を加えます。

Kerrゲートの特徴と原理

• 非線形性: Kerrゲートは、光の量子状態に非線形な変化をもたらします。これは、線形光学素子では達成できない特性です。
• 位相シフト:光の強度（または量子状態の特定の性質）に応じて、光の位相をシフトさせます。具体的には、光の強度に比例して位相が変わります。
• Kerr効果の利用: Kerrゲートは、物質が示すKerr効果（非線形光学効果の一つ）を利用します。これにより、光の強度によってその物質の屈折率が変化し、それが位相シフトに寄与します。

Kerrゲートの応用

• 量子計算: Kerrゲートは、特定の量子計算アルゴリズムにおいて重要な役割を果たします。非線形性により、量子もつれの生成や複雑な量子状態の操作が可能になります。
• 量子通信: 量子暗号や量子通信の分野では、Kerrゲートを使用して特定の量子状態の制御や検証を行うことができます。
• 量子エラー訂正: 量子エラー訂正のスキームにおいても、Kerrゲートの非線形性が役立ちます。

技術的課題

• 実装の難しさ: Kerr効果は通常非常に微弱であり、効果的なKerrゲートの実装は技術的に困難です。
• 高度な光学素子や特殊な物質が必要になることがあります。

Kerrゲートは、その非線形性と量子状態に対するユニークな操作能力により、光量子コンピューティングの分野で注目されています。しかし、その実装と制御は依然として挑戦的な課題です。

重みの初期化と設定

QNNの重みは、TensorFlowの変数として初期化されます。init_weights関数は、アクティブ（非線形）パラメータとパッシブ（線形）パラメータに異なる標準偏差を使用してランダムに重みを生成します。

重みについては、下記の、Replacing numbers with Tensors、の記事を一読する必要があります。

数値をシンボリックパラメータにバインドする必要があります。シンボリックパラメータに数値をバインドするためには、エンジンを実行する際にargsキーワード引数を使用して、パラメータ名から値へのマッピングを渡します。サンプルの例では、

def cost(weights):
    # Create a dictionary mapping from the names of the Strawberry Fields
    # symbolic gate parameters to the TensorFlow weight values.
    mapping = {p.name: w for p, w in zip(sf_params.flatten(), tf.reshape(weights, [-1]))}

    # run the engine
    state = eng.run(qnn, args=mapping).state

の部分に相当します。mappingは何かというと、

 mapping =  
{'0': <tf.Tensor: shape=(), dtype=float32, numpy=-0.07355491>, 
 '1': <tf.Tensor: shape=(), dtype=float32, numpy=4.845072e-05>, 
 '47': <tf.Tensor: shape=(), dtype=float32, numpy=-5.5957036e-05>}:

のように、辞書で、'0'という名前のkeyが、tf.Tensorの一つの値に対応しています。これをどこで使っているかというと、

# Create array of Strawberry Fields symbolic gate arguments, matching
# the size of the weights Variable.
sf_params = np.arange(num_params).reshape(weights.shape).astype(np.str)
sf_params = np.array([qnn.params(*i) for i in sf_params])

# Construct the symbolic Strawberry Fields program by
# looping and applying layers to the program.
with qnn.context as q:
    for k in range(layers):
        layer(sf_params[k], q)

の部分で、パラメータを設定しています。qnn.params(i)のは引数のアンパックの操作で、params の関数は下記のように単に変数を登録しているだけです。

このあたりの仕様はややこしいですが、、tensorflowと連携するために必要なおまじないなのでしょう。

最適化プロセス

最適化の目的は、QNNの出力状態が目標状態（ここでは単一光子状態）と一致するように重みを調整することです。cost関数は、出力状態と目標状態の違い（loss）と忠実度（fidelity）を計算します。TensorFlowのオプティマイザーを使用して、これらの重みを反復的に更新し、目標状態に近づけていきます。

忠実度 (fidelity) は、 $f(w)=\left\langle\psi(w) \mid \psi_t\right\rangle$ として定義されます。これは、我々の QNN の出力状態ベクトル $|\psi(w)\rangle$ と、ターゲット状態 $\mid \left.\psi_t\right\rangle$ の内積で定義されます。この２つの差ベクトルの絶対値 $\left|\psi(w)-\psi_t\right|$ は、diffrence という変数名で計算しています。

def cost(weights):
...
    return difference, fidelity, ket, tf.math.real(state.trace())
# cost 関数の最初の戻り値は difference 
# 最適化の部分で、
        loss, fid, _, trace = cost(weights)
# としているので、loss = difference である。

という使い方をしているので、diffrence を最小化するようにパラメータを更新している。fidelityはあくまで評価にしか用いていません。traceは、このプログラムでは積極的に使っていませんが、 Fock-basis の cutoff の次元が小さいと誤差が大きくなり、trace が 1 よりも大きく外れるので、cutoff 次元の良さを確認するために存在しています。

プログラム

TensorFlowの警告を無視する設定

# TensorFlowの警告を無視する設定
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

これは理由は不明だが、、逆微分の時に型変換で出るwarningを止めるためのおまじない。2023.11.27時点では、対処法はこれしかないようです。

実行例

にgoogle colab上での実行例を置いています。

全コード

#!/usr/bin/env python3
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

# TensorFlowの警告を無視する設定
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)

import strawberryfields as sf
from strawberryfields import ops

# =========================================================================
# Utility functions
# =========================================================================

# define interferometer
def interferometer(params, q):
    """Parameterised interferometer acting on ``N`` modes.
       Nモードに作用するパラメータ化されたインターフェロメーター。

    Args:
        params (list[float]): list of length ``max(1, N-1) + (N-1)*N`` parameters.
        ビームスプリッターの角度、位相、局所回転のパラメーターのリスト

            * The first ``N(N-1)/2`` parameters correspond to the beamsplitter angles
            * The second ``N(N-1)/2`` parameters correspond to the beamsplitter phases
            * The final ``N-1`` parameters correspond to local rotation on the first N-1 modes

        q (list[RegRef]): list of Strawberry Fields quantum registers the interferometer
            is to be applied to
       Strawberry Fieldsの量子レジスターのリスト

    """
    N = len(q)
    theta = params[: N * (N - 1) // 2]
    phi = params[N * (N - 1) // 2 : N * (N - 1)]
    rphi = params[-N + 1 :]

    if N == 1:
        # the interferometer is a single rotation
        ops.Rgate(rphi[0]) | q[0]
        return

    n = 0  # keep track of free parameters

    # Apply the rectangular beamsplitter array 長方形のビームスプリッター配列の適用
    # The array depth is N
    for l in range(N):
        for k, (q1, q2) in enumerate(zip(q[:-1], q[1:])):
            # skip even or odd pairs depending on layer
            if (l + k) % 2 != 1:
                ops.BSgate(theta[n], phi[n]) | (q1, q2)
                n += 1

    # apply the final local phase shifts to all modes except the last one
    # 最後のモードを除く全モードに局所位相シフトを適用
    for i in range(max(1, N - 1)):
        ops.Rgate(rphi[i]) | q[i]
    # Rgate only applied to first N - 1 modes

# define layer
def layer(params, q):
    """CV quantum neural network layer acting on ``N`` modes.
       Nモードに作用するCV量子ニューラルネットワークレイヤー。

    Args:
        params (list[float]): list of length ``2*(max(1, N-1) + N**2 + n)`` containing
            the number of parameters for the layer
        q (list[RegRef]): list of Strawberry Fields quantum registers the layer
            is to be applied to
    """
    N = len(q)
    M = int(N * (N - 1)) + max(1, N - 1)

    int1 = params[:M]
    s = params[M : M + N]
    int2 = params[M + N : 2 * M + N]
    dr = params[2 * M + N : 2 * M + 2 * N]
    dp = params[2 * M + 2 * N : 2 * M + 3 * N]
    k = params[2 * M + 3 * N : 2 * M + 4 * N]

    # begin layer
    interferometer(int1, q)

    for i in range(N):
        ops.Sgate(s[i]) | q[i]

    interferometer(int2, q)

    for i in range(N):
        ops.Dgate(dr[i], dp[i]) | q[i]
        ops.Kgate(k[i]) | q[i]
    # end layer

def init_weights(modes, layers, active_sd=0.0001, passive_sd=0.1):
    """Initialize a 2D TensorFlow Variable containing normally-distributed
    random weights for an ``N`` mode quantum neural network with ``L`` layers.

    Args:
        modes (int): the number of modes in the quantum neural network
        layers (int): the number of layers in the quantum neural network
        active_sd (float): the standard deviation used when initializing
            the normally-distributed weights for the active parameters
            (displacement, squeezing, and Kerr magnitude)
        passive_sd (float): the standard deviation used when initializing
            the normally-distributed weights for the passive parameters
            (beamsplitter angles and all gate phases)

    Returns:
        tf.Variable[tf.float32]: A TensorFlow Variable of shape
        ``[layers, 2*(max(1, modes-1) + modes**2 + modes)]``, where the Lth
        row represents the layer parameters for the Lth layer.
    """
    # Number of interferometer parameters:
    M = int(modes * (modes - 1)) + max(1, modes - 1)

    # Create the TensorFlow variables
    int1_weights = tf.random.normal(shape=[layers, M], stddev=passive_sd)
    s_weights = tf.random.normal(shape=[layers, modes], stddev=active_sd)
    int2_weights = tf.random.normal(shape=[layers, M], stddev=passive_sd)
    dr_weights = tf.random.normal(shape=[layers, modes], stddev=active_sd)
    dp_weights = tf.random.normal(shape=[layers, modes], stddev=passive_sd)
    k_weights = tf.random.normal(shape=[layers, modes], stddev=active_sd)

    weights = tf.concat(
        [int1_weights, s_weights, int2_weights, dr_weights, dp_weights, k_weights], axis=1
    )
    weights = tf.Variable(weights)

    return weights

# =========================================================================
# Define the optimization problem
# =========================================================================

# set the random seed
tf.random.set_seed(137)
np.random.seed(137)

# define width and depth of CV quantum neural network
modes = 1
layers = 8
cutoff_dim = 6

# defining desired state (single photon state) 目標状態（単一光子状態）の定義
target_state = np.zeros(cutoff_dim)
target_state[1] = 1
target_state = tf.constant(target_state, dtype=tf.complex64)

# initialize engine and program
eng = sf.Engine(backend="tf", backend_options={"cutoff_dim": cutoff_dim})
qnn = sf.Program(modes)

# initialize QNN weights
weights = init_weights(modes, layers)
num_params = np.prod(weights.shape)

# Create array of Strawberry Fields symbolic gate arguments, matching
# the size of the weights Variable.
sf_params = np.arange(num_params).reshape(weights.shape).astype(np.str)
sf_params = np.array([qnn.params(*i) for i in sf_params])

# Construct the symbolic Strawberry Fields program by
# looping and applying layers to the program.
with qnn.context as q:
    for k in range(layers):
        layer(sf_params[k], q)

def safe_abs(x): # Strawberry Fieldsのシンボリックゲート引数の配列を作成
    # Helper function to deal with tensor terms near zero

    # Check where we have near zero terms
    EPS = 1e-15
    x = tf.where(tf.abs(x) < EPS, tf.zeros_like(x), x)
    zero = tf.constant(0, dtype=tf.complex64)
    x_ok = tf.not_equal(x, zero)

    # To make sure, swap out the zeros with ones
    safe_x = tf.where(x_ok, x, tf.ones_like(x, dtype=tf.complex64))
    return tf.where(x_ok, tf.abs(safe_x), tf.zeros_like(x, dtype=tf.float32))

def cost(weights):
    # Create a dictionary mapping from the names of the Strawberry Fields
    # symbolic gate parameters to the TensorFlow weight values.
    mapping = {p.name: w for p, w in zip(sf_params.flatten(), tf.reshape(weights, [-1]))}

    # run the engine
    state = eng.run(qnn, args=mapping).state
    ket = state.ket()

    difference = tf.reduce_sum(safe_abs(ket - target_state))
    fidelity = tf.abs(tf.reduce_sum(tf.math.conj(ket) * target_state)) ** 2
    return difference, fidelity, ket, tf.math.real(state.trace())

# set up optimizer
opt = tf.keras.optimizers.Adam()
cost_before, fidelity_before, _, _ = cost(weights)
print("Beginning optimization")

# 学習の進捗を記録するためのリスト
fidelities = []
losses = []

# Perform the optimization
N_epoch = 1000
for i in range(N_epoch):
    # reset the engine if it has already been executed
    if eng.run_progs:
        eng.reset()

    with tf.GradientTape() as tape:
        loss, fid, _, trace = cost(weights)
        fidelities.append(fid.numpy())
        losses.append(loss.numpy())
    # one repetition of the optimization
    gradients = tape.gradient(loss, weights)
    opt.apply_gradients(zip([gradients], [weights]))

    # Prints progress at every rep
    if i % 1 == 0:
        print("Rep: {} Cost: {:.4f} Fidelity: {:.4f} Trace: {:.4f}".format(i, loss, fid, trace))

cost_after, fidelity_after, ket_after, _ = cost(weights)
print("\nFidelity before optimization: ", fidelity_before.numpy())
print("Fidelity after optimization: ", fidelity_after.numpy())
print("\nTarget state: ", target_state.numpy())
print("Output state: ", np.round(ket_after.numpy(), decimals=3))

# 学習の loss を可視化
plt.plot(losses)
plt.xlabel('Iteration')
plt.ylabel('Loss')
plt.title('Learning Progress')
plt.show()
# 学習の fidelity を可視化
plt.plot(fidelities)
plt.xlabel('Iteration')
plt.ylabel('Fidelity')
plt.title('Learning Progress')
plt.show()

学習結果

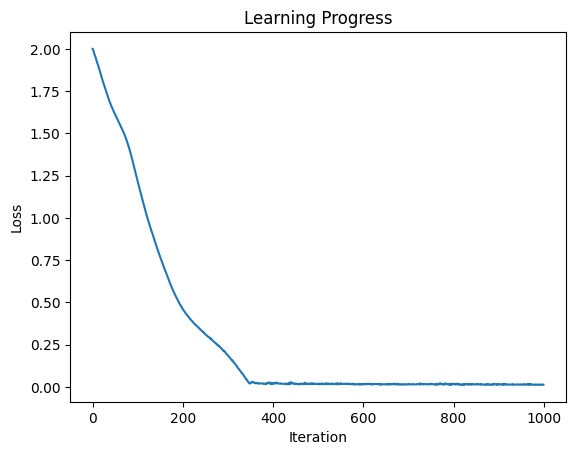
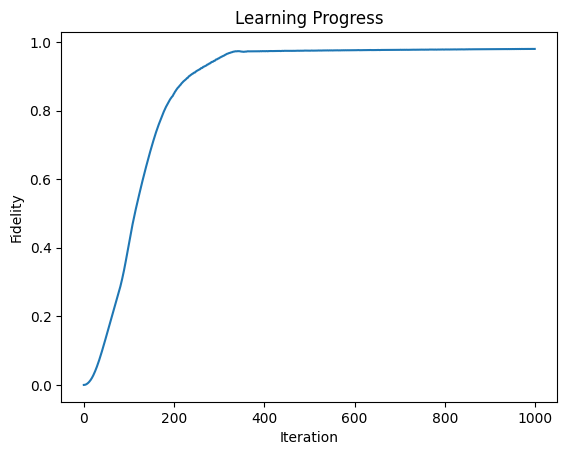
学習曲線は下記のようになります。

これで、lossが0に下がり、fidelityが1に漸近していることが確認できます。初期ベクトルを与えて、ランダムな初期状態から初期ベクトルに近づける、という簡単な問題ですが、確実に動く例として、Strawberryfiledsのご本家のサンプルが提供されてるのだと思います。

参考文献

大元の記事で引用されてる参考文献です。

• Nathan Killoran, Thomas R Bromley, Juan Miguel Arrazola, Maria Schuld, Nicolás Quesada, and Seth Lloyd. Continuous-variable quantum neural networks. arXiv preprint arXiv:1806.06871, 2018.

• Maria Schuld, Ville Bergholm, Christian Gogolin, Josh Izaac, and Nathan Killoran. Evaluating analytic gradients on quantum hardware. Physical Review A, 99(3):032331, 2019.

• William R Clements, Peter C Humphreys, Benjamin J Metcalf, W Steven Kolthammer, and Ian A Walsmley. Optimal design for universal multiport interferometers. Optica, 3(12):1460–1465, 2016. doi:10.1364/OPTICA.3.001460.