量子機械学習 PennyLane で IRISの分類問題を google Colab でやってみた

はじめに

単純な量子ニューラルネットワークを使用してIRISデータの3クラス分類を行う例を紹介します。
ただし、量子回路の構造や損失関数の定義は多岐にわたり、実際の応用や実験に応じてさまざまな変更や拡張が必要です。特に、量子コンピュータは、現時点では高次元データを直接処理するのは難しいです。

Pennylaneの標準的な量子ビットシミュレータ（default.qubit）を使用した例になります(このシミュレータは古典的なコンピュータ上で動作します)。

Google colab 上で動くサンプルになりますので、コードを見ればわかる方はこちらを参照ください。

この記事では、最もシンプルなコードの例を最初に紹介します。その次に、 qml.templates.StronglyEntanglingLayers と qml.templates.AngleEmbedding を用いた例を紹介します。この例を通じて、量子機械学習について考えるキッカケになれば幸いです。

量子機械学習のメリットの説明

IRISデータの3クラス分類、を量子機械学習でやって何になるのか？というツッコミがありそうなので、メリットの説明をしておきます。

量子機械学習は、「量子状態のエンコーディング」、「量子ゲートの使用」、「量子エンタングルメントの利用」など、量子力学の特性の活用が大切です。
ただし、その利点が特に顕在化するには、その環境が成熟することが必要です。

具体的には、「量子ハードウェア (実際の量子コンピュータ、NISQ（ノイズがほどほどの）デバイス)など」「量子的なデータ(量子系特有のデータ。量子化学計算や量子センサーなど)」「高次元/複雑な問題(量子コンピュータが指数的に速く解を見つけられる問題)」など、能力が発揮できるにはその舞台が整うことが必要です。

量子機械学習の真の強みや利点を生み出すためには、量子計算の基本的な原理や特性を活用するアルゴリズムや手法に慣れることも大切です。この記事では、簡単な問題を量子機械学習で解くことを通じて、量子の利点を模索していくスタートラインとなれば幸いです、という感じです。

量子機械学習 PennyLane で IRISの分類問題を解く例 (基礎編)

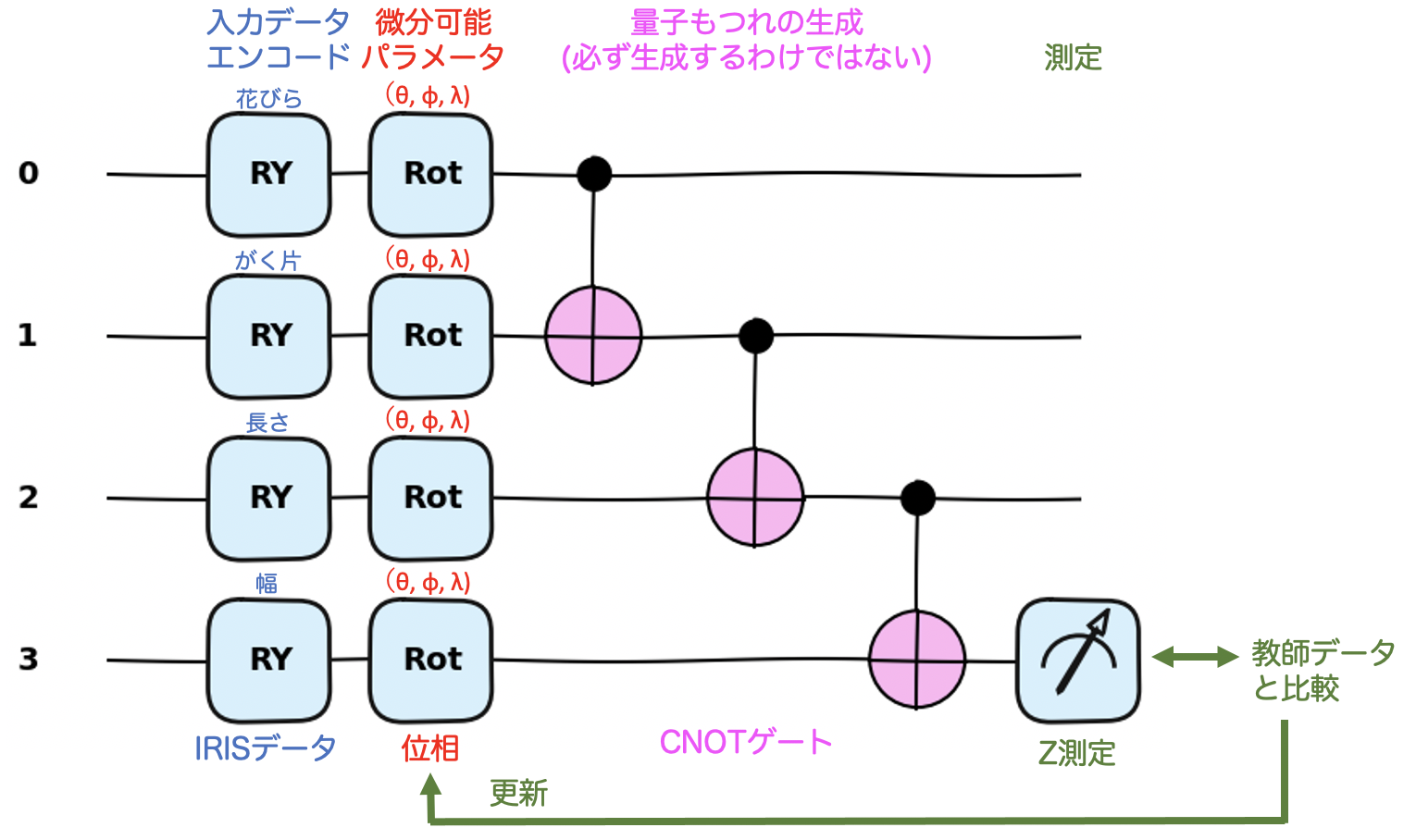
量子機械学習部分の模式図

ここで紹介する量子回路は、4量子ビットの量子回路を使用して、下記の４ステップからなります。

1. 4次元のIRISデータをY方向で表現します。
2. 4量子ビットに回転を施し(具体的には(θ、ϕ、λ）を取り、それぞれx、y、z軸周りの回転)、これらが連続量で滑らかで微分可能であることを利用します。
3. 量子回路特有のエンタングルメントを引き起こすために CNOT を全体に作用させます。
4. 最後に、測定を行い、教師データの答えとの答え合せをし、必要な修正をパラメータに施します。これが収束するまで続けます。

これを図示すると、下記になります。

ソースコード

pennylane_iris_kiso.py

# -*- coding: utf-8 -*-
"""PennyLane_IRIS_kiso.ipynb

Automatically generated by Colaboratory.

Original file is located at
    https://colab.research.google.com/drive/115pxiPV1kZ-ahl0qeqFoVrB_XX_NQhFr
"""

!pip install pennylane

# 必要なライブラリとモジュールをインポート
import pennylane as qml
from pennylane import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

# IRISデータセットをロード
data = datasets.load_iris()
X = data.data  # 特徴量
y = data.target  # ラベル

print("X = ", X[0:3])
print("y = ", y[0:3])

# 特徴量の標準化（平均0、標準偏差1にスケーリング）
scaler = StandardScaler().fit(X)
X_scaled = scaler.transform(X)

print("X_scaled = ", X_scaled[0:3])

# データをトレーニング用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

# Pennylaneの量子デバイスを設定（4量子ビットのシミュレータ）
n_wires = 4
dev = qml.device('default.qubit', wires=n_wires)

# 量子回路の定義
@qml.qnode(dev)
def quantum_circuit(x, w):
    # 入力データを量子ビットに埋め込む
    for i in range(n_wires):
        qml.RY(x[i], wires=i)
    # パラメータで回転させる
    for i, weights_for_wire in enumerate(w):
        qml.Rot(*weights_for_wire, wires=i)
    # 量子ビットをエンタングルさせる
    qml.CNOT(wires=[0, 1])
    qml.CNOT(wires=[1, 2])
    qml.CNOT(wires=[2, 3])
    # 最後の量子ビットの期待値を返す
    return qml.expval(qml.PauliZ(3))

# 量子回路の確認
qml.drawer.use_style("pennylane")
fig, ax = qml.draw_mpl(quantum_circuit)( [0.1, 0.2, 0.3, 0.4],np.random.randn(4,3))
fig.show()
print(qml.draw(quantum_circuit, expansion_strategy="device")([0.1, 0.2, 0.3, 0.4], np.random.randn(4,3)))

# 量子ニューラルネットワークの出力を計算
def quantum_neural_net(var, x):
    return np.array([quantum_circuit(x, w) for w in var])

# コスト関数（予測と実際のラベルとの二乗誤差の平均）
def cost(var, X, y):
    predictions = np.array([quantum_neural_net(var, x) for x in X])
    return np.mean(np.sum((predictions - y)**2, axis=1))

# 勾配降下法を使用するオプティマイザを設定
optimizer = qml.GradientDescentOptimizer(stepsize=0.1)
num_epochs = 30
batch_size = 10

# 量子回路のパラメータをランダムに初期化
var_init = np.random.randn(3, n_wires, 3)  # (クラス数, ワイヤー数, パラメータ数)
var = var_init

# ラベルをone-hotエンコーディング形式に変換
y_train_onehot = np.zeros((y_train.size, y_train.max()+1))
y_train_onehot[np.arange(y_train.size), y_train] = 1

# トレーニングループ
for epoch in range(num_epochs):
    # ミニバッチごとに学習
    for i in range(0, len(X_train), batch_size):
        X_batch = X_train[i:i+batch_size]
        y_batch = y_train_onehot[i:i+batch_size]
        # パラメータの更新
        var = optimizer.step(lambda v: cost(v, X_batch, y_batch), var)

    # テストデータでの予測と評価
    predictions = np.array([quantum_neural_net(var, x) for x in X_test])
    # 予測結果と実際のラベルとの比較で精度を計算
    accuracy = np.mean(np.argmax(predictions, axis=1) == y_test)
    # 精度を表示
    print(f"Epoch {epoch + 1}, Accuracy: {accuracy:.4f}")

# 最終結果の確認
# テストデータでの予測と評価
predictions = np.array([quantum_neural_net(var, x) for x in X_test])
# 予測結果と実際のラベルとの比較で精度を計算
print(" predictions[0:3] = ", predictions[0:3])
print(" np.argmax(predictions[0:3], axis=1) = ", np.argmax(predictions[0:3], axis=1))
print(" y_test[0:3] = ", y_test[0:3])
accuracy = np.mean(np.argmax(predictions, axis=1) == y_test)
# 精度を表示
print(f"Epoch {epoch + 1}, Accuracy: {accuracy:.4f}")

実行結果

このサンプルを走らせると、

0: ──RY(0.10)──Rot(0.00,-0.69,-3.05)─╭●───────┤     
1: ──RY(0.20)──Rot(0.05,0.46,-0.81)──╰X─╭●────┤     
2: ──RY(0.30)──Rot(-1.87,-0.23,0.68)────╰X─╭●─┤     
3: ──RY(0.40)──Rot(0.97,0.34,-0.71)────────╰X─┤  <Z>

Epoch 1, Accuracy: 0.5333
Epoch 2, Accuracy: 0.5778
...
Epoch 27, Accuracy: 0.7556
Epoch 28, Accuracy: 0.7556
Epoch 29, Accuracy: 0.7556
Epoch 30, Accuracy: 0.7556

このような結果になります。数分くらいの計算時間で、現状だと精度もそこそこになります。

コードの解説

量子ビットの回転

    # パラメータで回転させる
    for i, weights_for_wire in enumerate(w):
        qml.Rot(*weights_for_wire, wires=i)

この部分についてです。

量子機械学習においては、パラメータの回転は、変分量子回路の中で重要なパーツになります。その理由としては、下記の３つになります。

• 変分性
  • 量子機械学習のモデルは「変分的」、つまり、モデルのパラメータを変化させることで、量子回路の出力を連続的に変更できることが大切です。この変分性を備えることで、勾配降下法などの最適化アルゴリズムを使用してモデルをトレーニングすることができます。
• エンタングルメントの生成
  • 回転ゲートと制御ゲート（CNOTなど）を組み合わせることで、量子ビット間のエンタングルメントが生成できます。
• 複雑な量子状態の生成
  • 回転ゲートにより、初期状態（通常は |0⟩ 状態、このサンプルでは入力データにより回転された状態）からより複雑な量子状態を生成できます。量子モデルが、複雑な関数やパターンを近似・学習する自由度をたつために必要です。

CNOTゲートの役割

CNOTゲートがエンタングルメントを生成するかどうかは、ゲートを適用する前の量子ビットの初期状態に依存します。

• 制御ビットが |0⟩ の場合: CNOTゲートはターゲットビットに何も影響を与えません。したがって、もともとの状態が separable state （つまりエンタングルしていない状態）である場合、ゲートの適用後も separable state のままです。

• 制御ビットが |1⟩ の場合: CNOTゲートはターゲットビットにXゲート（ビット反転）を適用します。この場合、もともとの状態が separable state であると、エンタングル状態が生成される可能性があります。

より詳細は、web 上にいろんな方が解説されてるので、そちらを参考にしてください。

最適化されるパラメータ

# 量子回路のパラメータをランダムに初期化
var_init = np.random.randn(3, n_wires, 3)  # (クラス数, ワイヤー数, パラメータ数)
var = var_init

の部分の説明です。

特に、var_init = np.random.randn(3, n_wires, 3) という行の中で、配列の形状が (3, n_wires, 3) となっている部分についてです。

この配列は、量子回路のパラメータを保持します。IRISデータセットは3つのクラス（0, 1, 2をラベルとして持つ）での分類問題なので、クラスごとに異なる量子回路のパラメータセットを持ち、各クラスに対する量子回路の出力（または予測）が最適化されることを期待しています。

配列の各次元は以下の意味を持っています：

• 第1次元 (3): クラス数。これはIRISデータセットの3つのクラス（setosa, versicolor, virginica）に対応しています。各クラスにはそれぞれ独自のパラメータセットが存在します。
• 第2次元 (n_wires): ワイヤー数（または量子ビット数）。この例では4としています。この次元は、量子回路内の各量子ビットに対応するパラメータを持っています。
• 第3次元 (3): パラメータ数。qml.Rot ゲートは3つのパラメータ (θ、φ、λ) を必要とするので、この次元はその3つのパラメータに対応しています。

このようにして、var_init はランダムな初期値を持つ3D配列として定義され、各クラスごと、各ワイヤーごと、各ワイヤー内の各ゲートごとに異なるパラメータを持つことになります。

全部でパラメータ数は、

第1次元 (3): クラス数 x 第2次元 (4): 量子ビット数 x 第3次元 (3): 回転のパラメータ数
= 3 x 4 x 3 = 36 個

となります。

量子機械学習 PennyLane で IRISの分類問題を解く例 (応用編)

AngleEmbedding と StronglyEntanglingLayers の利用

の後半に、AngleEmbedding と StronglyEntanglingLayers の利用した例を紹介しています。

具体的な変更箇所は下記の箇所だけです。

# 量子回路の定義
@qml.qnode(dev)
def quantum_circuit(x, w):
    # 入力データを量子ビットに埋め込む
    qml.templates.AngleEmbedding(x, wires=range(n_wires))
    # Strongly entangling layers
    qml.templates.StronglyEntanglingLayers(w, wires=range(n_wires))
    # 最後の量子ビットの期待値を返す
    return qml.expval(qml.PauliZ(3))

# 量子回路の確認
n_layers = 4
fig, ax = qml.draw_mpl(quantum_circuit)( [0.1, 0.2, 0.3, 0.4], np.random.randn(3, n_layers, n_wires, 3))
fig.show()
print(qml.draw(quantum_circuit, expansion_strategy="device")([0.1, 0.2, 0.3, 0.4], np.random.randn(3, n_layers, n_wires, 3)))

の部分です。

    # 入力データを量子ビットに埋め込む
    for i in range(n_wires):
        qml.RY(x[i], wires=i)

の部分が、qml.templates.AngleEmbedding(x, wires=range(n_wires)) に置き換わり、

# パラメータで回転させる
    for i, weights_for_wire in enumerate(w):
        qml.Rot(*weights_for_wire, wires=i)
    # 量子ビットをエンタングルさせる
    qml.CNOT(wires=[0, 1])
    qml.CNOT(wires=[1, 2])
    qml.CNOT(wires=[2, 3])

の部分が、qml.templates.StronglyEntanglingLayers(w, wires=range(n_wires)) に変わっています。

基本的に同じですが、コードがシンプルになり、より強力なエンタングルメントを持つ量子回路を構築することができます。ただし、最適化の振る舞いや収束性は変更になる可能性があるので、注意が必要です。

qml.StronglyEntanglingLayers の詳細

PennyLane の qml.StronglyEntanglingLayers の実装については、

に詳細が書かれています。源泉のアイディアは、

の図４にあるように、近い qubit と遠い qubit をほどよく混ぜることがよい、という話しがあり、それに基づいて実装されているようです。

qml.StronglyEntanglingLayers は、エンタングルメントを強く導入するためのテンプレートの一つで、具体的には、各レイヤーにおいて全ての量子ビットのペア間でエンタングルメントを生成します。ゲートの各レイヤーで全ての隣接する量子ビットペアに対してエンタングルメントゲート（例えば、CNOT）を適用し、さらに次のレイヤーで量子ビットの順序をローテーションして同様のエンタングルメントを適用します。これにより、複数のレイヤーを通じて全ての量子ビット間のエンタングルメントが強化されます。

ソースコード (StronglyEntanglingLayersを利用)

# 必要なライブラリとモジュールをインポート
import pennylane as qml
from pennylane import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# -*- coding: utf-8 -*-

# IRISデータセットをロード
data = datasets.load_iris()
X = data.data  # 特徴量
y = data.target  # ラベル

print("X = ", X[0:3])
print("y = ", y[0:3])

# 特徴量の標準化（平均0、標準偏差1にスケーリング）
scaler = StandardScaler().fit(X)
X_scaled = scaler.transform(X)

print("X_scaled = ", X_scaled[0:3])

# データをトレーニング用とテスト用に分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)

# Pennylaneの量子デバイスを設定（4量子ビットのシミュレータ）
n_wires = 4
dev = qml.device('default.qubit', wires=n_wires)

# 量子回路の定義
@qml.qnode(dev)
def quantum_circuit(x, w):
    # 入力データを量子ビットに埋め込む
    qml.templates.AngleEmbedding(x, wires=range(n_wires))
    # Strongly entangling layers
    qml.templates.StronglyEntanglingLayers(w, wires=range(n_wires))
    # 最後の量子ビットの期待値を返す
    return qml.expval(qml.PauliZ(3))

# 量子回路の確認
n_layers = 4
fig, ax = qml.draw_mpl(quantum_circuit)( [0.1, 0.2, 0.3, 0.4], np.random.randn(3, n_layers, n_wires, 3))
fig.show()
print(qml.draw(quantum_circuit, expansion_strategy="device")([0.1, 0.2, 0.3, 0.4], np.random.randn(3, n_layers, n_wires, 3)))

# 量子ニューラルネットワークの出力を計算
def quantum_neural_net(var, x):
    return np.array([quantum_circuit(x, w) for w in var])

# コスト関数（予測と実際のラベルとの二乗誤差の平均）
def cost(var, X, y):
    predictions = np.array([quantum_neural_net(var, x) for x in X])
    return np.mean(np.sum((predictions - y)**2, axis=1))

# 勾配降下法を使用するオプティマイザを設定
optimizer = qml.GradientDescentOptimizer(stepsize=0.1)
num_epochs = 8
batch_size = 10

# 量子回路のパラメータをランダムに初期化
var_init_strong = np.random.randn(3, n_layers, n_wires, 3)  # (クラス数, レイヤー数, ワイヤー数, パラメータ数)
var_strong = var_init_strong

print("var_init_strong.shape = ", var_init_strong.shape)

# ラベルをone-hotエンコーディング形式に変換
y_train_onehot = np.zeros((y_train.size, y_train.max()+1))
y_train_onehot[np.arange(y_train.size), y_train] = 1

# トレーニングループ
for epoch in range(num_epochs):
    # ミニバッチごとに学習
    for i in range(0, len(X_train), batch_size):
        X_batch = X_train[i:i+batch_size]
        y_batch = y_train_onehot[i:i+batch_size]
        # パラメータの更新
        var_strong = optimizer.step(lambda v: cost(v, X_batch, y_batch), var_strong)

    # テストデータでの予測と評価
    predictions = np.array([quantum_neural_net(var_strong, x) for x in X_test])
    # 予測結果と実際のラベルとの比較で精度を計算
    accuracy = np.mean(np.argmax(predictions, axis=1) == y_test)
    # 精度を表示
    print(f"Epoch {epoch + 1}, Accuracy: {accuracy:.4f}")

# 最終結果の確認
# テストデータでの予測と評価
predictions = np.array([quantum_neural_net(var_strong, x) for x in X_test])
# 予測結果と実際のラベルとの比較で精度を計算
print(" predictions[0:3] = ", predictions[0:3])
print(" np.argmax(predictions[0:3], axis=1) = ", np.argmax(predictions[0:3], axis=1))
print(" y_test[0:3] = ", y_test[0:3])
accuracy = np.mean(np.argmax(predictions, axis=1) == y_test)
# 精度を表示
print(f"Epoch {epoch + 1}, Accuracy: {accuracy:.4f}")

実行結果

実行すると、1 Epoch に数分程度の時間がかかるようになるが、精度は向上する。

0: ──RX(0.10)──Rot─╭●───────╭X──Rot─╭●────╭X──Rot──────╭●─╭X───────┤     
1: ──RX(0.20)──Rot─╰X─╭●────│───Rot─│──╭●─│──╭X────Rot─│──╰●─╭X────┤     
2: ──RX(0.30)──Rot────╰X─╭●─│───Rot─╰X─│──╰●─│─────Rot─│─────╰●─╭X─┤     
3: ──RX(0.40)──Rot───────╰X─╰●──Rot────╰X────╰●────Rot─╰X───────╰●─┤  <Z>
var_init_strong.shape =  (3, 4, 4, 3)
Epoch 1, Accuracy: 0.7556
Epoch 2, Accuracy: 0.8889
Epoch 3, Accuracy: 0.9333
Epoch 4, Accuracy: 0.9778
Epoch 5, Accuracy: 1.0000
Epoch 6, Accuracy: 1.0000
Epoch 7, Accuracy: 1.0000
Epoch 8, Accuracy: 1.0000

これで、精度が 100%!!なので、量子機械学習はすごい！と思うのは早計です。

SronglyEntanglingLayersは、各レイヤーに n_wires 回の回転（Rotゲートで3つのパラメータ）と n_wires-1 のエンタングルメント（パラメータなしのCNOTゲート）が必要です。複数のStronglyEntanglingLayersをスタックする場合、例えばn_layers のレイヤーを使用する場合、必要なパラメータの総数は n_layers倍になります。

ここで用いているパラーメタの数は、

var_init_strong.shape =  (3, 4, 4, 3)
# (クラス数, レイヤー数, ワイヤー数, パラメータ数)

なので、3 x 4 x 4 x 3 = 144 個になります。IRISデータのデータ数は、150個なので、、それで精度が高いだけです。このように、問題に応じて、適切な深さや回路構造を考え、結果も慎重に判断するのが大切です。

上記の(クラス数, レイヤー数, ワイヤー数, パラメータ数)の、パラメータ数、というのは、

qml.Rot(θ1, θ2, θ3, wires=...)

これにより、Z-Y-Z回転をします。具体的には、

• 最初にθ1の周りにZ軸を中心に回転、
• 次にθ2の周りにY軸を中心に回転、
• 最後にθ3の周りにZ軸を中心に回転、

という順序で回転するので、３つのパラメータが必要になります。

ブロッホ球上の一点を指定するのに必要なパラメータは2つ(θとφ)ですが、任意の1量子ビットのユニタリ変換を指定するのには3つのパラメータが必要です。

まとめ

量子機械学習の例を IRIS データを用いて、簡単な例と、 Strongly Enganbling Layer を使って紹介しました。雰囲気を感じてもらえれば幸いです。

最後に、実装方法により、最適化の振る舞いや収束性が変わる、という点についてです。

• 収束の速さ: 量子回路の構造によって、学習が早くなるか、遅くなるか、あるいは就職性が劣化する可能性があります。そのため、学習率やオプティマイザの種類の調整が必要かもしれません。
• 局所的な最小値: エンタングルメントの構造や量子回路の深さが変わることで、コスト関数の形状も変わる可能性があります。これにより、新しい局所的な最小値にトラップされる可能性があるため、異なる初期値やオプティマイザの変更の検討も必要です。
• 過学習: より複雑な量子回路を使用することで、モデルがデータに過度に適合してしまい、新しいデータに対する汎化能力が低下する可能性があります。
• 計算時間: 回路構造により、計算コストが増加する可能性があります。特に、リアルな量子デバイスでの実験を考える場合、深い回路や多数のゲートはノイズの影響を受けやすくなります。
• ハイパーパラメータの調整: 回路により、最適なハイパーパラメータ（学習率、バッチサイズ、エポック数など）が異なる可能性があります。グリッドサーチやランダムサーチなどの手法を使って、新しいハイパーパラメータの組み合わせを探索も必要です。

これらのポイントも考慮し、新しい量子回路の設計や学習プロセスを慎重に検討することで、学習の効果を最大限に繋がると考えています。