はじめに
超伝導遷移端検出器(TES)の電熱フィードバックをLTspiceで行う簡単に行う方法について紹介します。
LTspiceは電気回路のシミュレーターであるが、集中定数として表現できるものは計算に乗せることができて、熱回路を離散的な電熱方程式として扱う場合には、熱もLTspiceで計算することができる。超伝導遷移端検出器は、電熱フィードバックで動作しており、これを例にとって、電熱フィードバックを含む回路をLTspiceで計算する方法について紹介する。
お手本としたのは、
The Spice simulatio of TES calorimeters, Miyazaki Toshiyuki. July 24, 2003
である。これを、LTspice XVII for OS X, BUild Nov 25 2020 Version:17.0.19.0 のGUIで簡単に動かせるように、宮崎etalの一部を改変したものを紹介する。
ちなみに、一部を改変した理由は、subcktを使うとmacのLTspiceだと一度保存して再び開いた時に回路を開けないというbug?があるのと、subcktの中はsubcktで触れないと最初は不便なためである。ここでは、subcktを一切使わず、ノイズの部分は一切割愛して、もっともシンプルにしたものを、電熱フィードバック(Electro Thermal Feedback;ETF) あり、ETFなしの違いを見える形で紹介します。
まずは動かしてみよう。
回路ファイルのダウンロード
だけダウンロードすればOK。LTspiceでこれを開きます。
一応、ネットリスト ltspice_tes_etf_single_pixel_qiita.cir もおいてあります。
LTspiceで開く
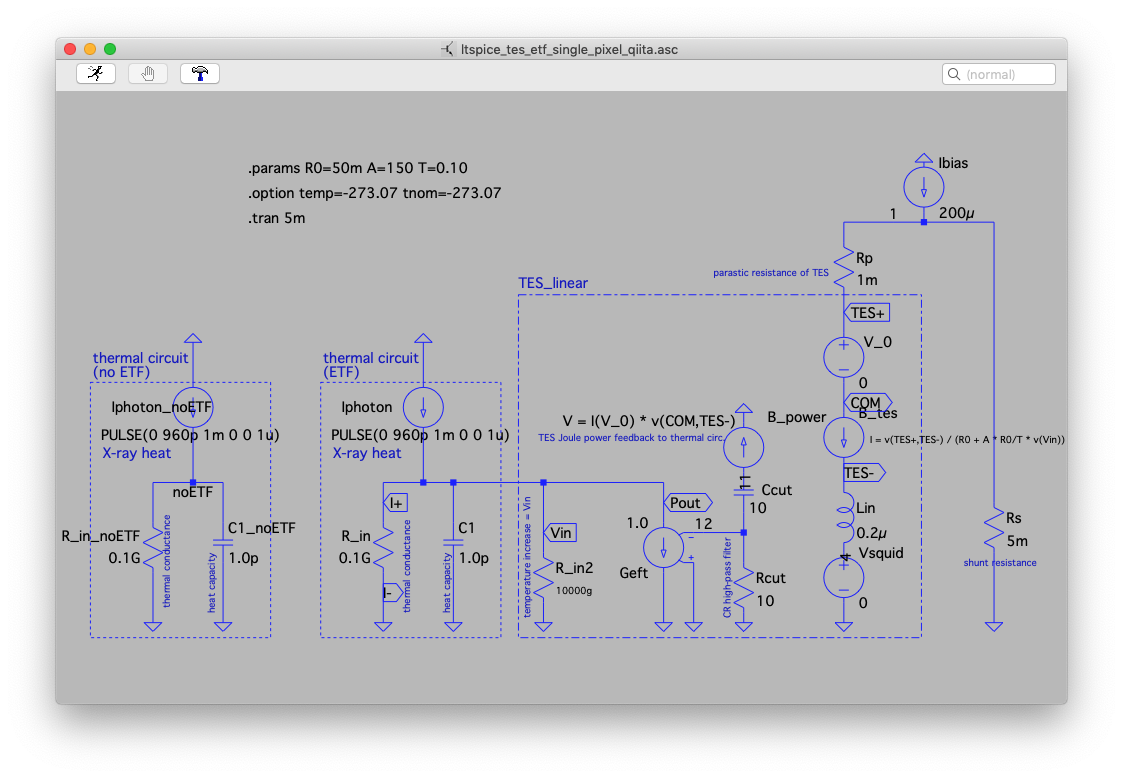
ltspice_tes_etf_single_pixel_qiita.asc をLTspiceで開こう。そうすると、
のような画面が出てくるはずである。
大きくは、ETF無しの熱回路(左)、ETFありの熱回路(中央)と電熱フィードバックでカップルしたTESの電気回路(右)となっている。
シミュレーションの実行
左上の走る人の姿のボタンを押して、シミュレーションを実行しよう。5msのシミュレーションが実行される。
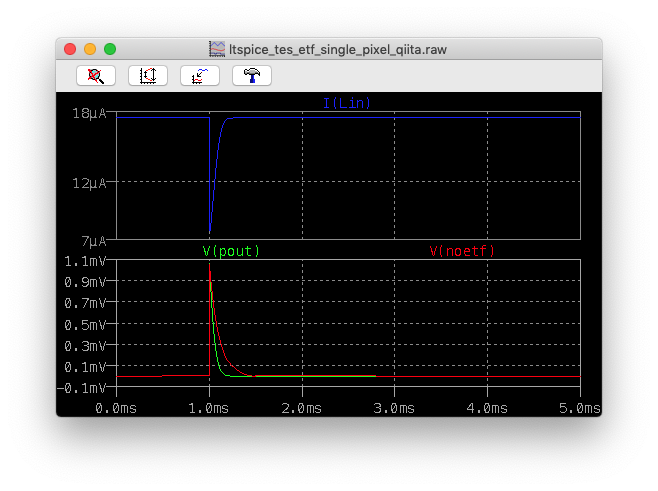
noETFとPoutを電圧プローブで触り、Linを電流プローブで触ってみよう。その上で、Add plot pane と grid を表示したのが、
である。V(pout)が電熱フィードバックがある時のパルスで、V(noeft)が電熱フィードバック無しのパルスである。I(Lin)がTESのインプットコイルに流れる電流である。
詳細説明
Spiceの超基本のおさらい
Spiceについてミニマム知っておくべきは、回路の情報はネットリストで記述される、ということ。そして、ネットリストの最初の文字、で何の素子であるかが決まる。逆に言えば、最初のアルファベットから素子が何かを暗記してないと、何がどう繋がってるのか分からない。
確認する場合は、LTspiceのマニュアル のP69-P70 の一覧をみてください。
今回、抵抗、コイル、コンデンサー以外で、重要なのは、
- B : 任意の動作信号源
- G : 電圧依存型の電流源
になります。
netlist
まずは、ネットリスト ltspice_tes_etf_single_pixel_qiita.cir を用いて紹介する。
名前の付け方は、極力、The Spice simulatio of TES calorimeters, Miyazaki Toshiyuki. July 24, 2003 を踏襲している。subcktを使わない分、名前が減っているとか、ノイズを入れる部分が無いなど少しだけ違う。
(下記、コメントを ; でつけますが、環境によっては動かない場合もあるらしいので注意してください。)
Ibias 0 1 200µ ; TESのDCバイアス電流源
Rs 1 0 5m ; シャント抵抗 5mΩ
Rp 1 TES+ 1m ; TESの寄生抵抗 1mΩ
Lin TES- 4 0.2µ ; TESのコイルのインダクタンス 1μH
Vsquid 4 0 0 ; 電圧源0の電圧源 (=電流計)
C1 Pout 0 1.0p ; 熱容量としてのコンデンサー 1pF
Iphoton 0 Pout PULSE(0 960p 1m 0 0 1u) ; X線の入力源としての電流パルス
R_in 0 Pout 0.1G ; 熱伝導率としての抵抗 0.1GΩ
R_in2 Pout 0 10000g ; 温度上昇に対応する電圧を測定するための抵抗 10000 GΩ
V_0 TES+ COM 0 ; 電圧0の電圧源(=電流計)
B_tes COM TES- I = V(TES+,TES-) / (R0 + A * R0/T * V(Pout)) ; TESの電流
B_power 11 0 V = I(V_0) * v(COM,TES-) ; TESのジュール発熱に相当する電圧を出力
Ccut 11 12 10 ; CR high pass filter の C 10F
Rcut 12 0 10 ; CR high pass filter の C 10Ω
Geft Pout 0 0 12 1.0; 0-12間の電圧を1.0倍してPout-0間に電流を出力する(feedback)
* ETFなしの熱回路。パラメータは上と同じ
C1_noETF noETF 0 1.0p;
Iphoton_noETF 0 noETF PULSE(0 960p 1m 0 0 1u)
R_in_noETF 0 noETF 0.1G
.tran 5m ; 5msecのシミュレーション
.option temp=-273.07 tnom=-273.07; 温度の設定(たぶん今は特に意味ない)
.params R0=50m A=150 T=0.10; R0=動作抵抗、A=温度計感度(所謂アルファ)、T=動作温度
熱回路
熱回路の基本要素は、
C1 Pout 0 1.0p ; 熱容量としてのコンデンサー 1pF
R_in 0 Pout 0.1G ; 熱伝導率としての抵抗 0.1GΩ
がメインである。C1が熱容量で、R_in の逆数が熱伝導度である。これを変えればパルスの時定数を変更することができる。ここでは、時定数は、熱伝導度 G = 1/R であることに注意して、
\tau \equiv \frac{C}{G} = CR = 1p \times 0.1G = 0.1 ~ \rm{ms}
という設定である。つまり、ETFがない場合の時定数は 0.1 msec となるように設定している。EFTが効くと、ループバックゲイン $\mathcal{L}$ を考慮する必要がある。このサンプルでは、ループバックゲイン $\mathcal{L}$ は、
\mathcal{L} = \frac{P_J \alpha}{GT} = \frac{ (15\times10^{-12}) \times150}{(10\times10^{-9})\times0.1} = 2.25
である。Pjは定常状態でのTESでのジュール発熱量、alphaは温度計感度、Gは熱伝導度、T0はTESの温度である。Pj = 15pW, 温度計感度alpha = 150, G = 1/R = 1/0.1G = 10e-9, TESの温度 T = 0.1 を用いている。
ループバックゲインの導出の詳細などは、 Transition-Edge Sensors, Irwin & Hilton を参考ください。
電流の変化がゼロの場合は、Transition-Edge Sensors, Irwin & Hiltonの式(18)より、
\tau_I \equiv \frac{\tau}{1 - \mathcal{L}} = \frac{\tau}{1 - \frac{P_J \alpha}{GT_0}} = \frac{\tau}{1 - 2.25} = -0.8 \tau
となり、この式を使うと時定数が負になってしまうので、電流の変化がゼロと仮定した近似式ではさすがに不十分なことがわかる。電流の変化がゼロだと仮定せずに電熱方程式を解くと、Transition-Edge Sensors, Irwin & Hiltonの式(29)となり、この式を電流依存性の$\beta$項はゼロとして使い、Rs = RL = 5mΩ、R_0 = 912nV/17.5uA (spiceで計測した値) = 52mΩ、を用いると、
\tau_{eff} \equiv \tau \frac{1 + \frac{R_L}{R_0}}{1+\frac{R_L}{R_0} + (1-\frac{R_L}{R_0}) \mathcal{L}} = \tau \frac{1 + \frac{0.005}{0.052}}{1+\frac{0.005}{0.052} + (1-\frac{0.005}{0.025}) 2.25} = 0.35 \tau
となる。Transition-Edge Sensors, Irwin & Hiltonの式(29)は、low inductance limit と呼ばれ、TESにカップルしているコイルのインダクタンスが小さい場合(この記事の例では0.2uH)に成り立つ。
では、実際に電流と電圧がX線パルスの前後でどう変化するか確認してみよう。
| バイアス電流 I_b | TES電流 I_tes | シャント抵抗電流 I_sh | シャント抵抗電圧V_sh | |
|---|---|---|---|---|
| X線が来る前 | 200 uA (固定) | 17.5uA | 182 uA | 912 nV |
| X線のピーク | 200 uA (固定) | 7.8 uA (~45%減) | 192 uA (~5%増) | 960nV (~5%増) |
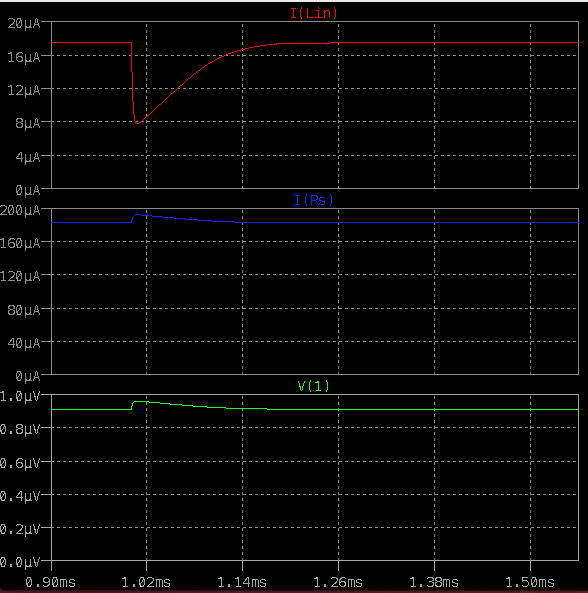
となっていて、実際にプローブした結果がこちらになります。
上から順に I(Lin)がTESを流れる電流、I(Rs)がシャント抵抗を流れる電流、V(1)がTESおよびシャント抵抗にかかる電圧である。時定数は0.02msくらいであり、ETF無しの時の0.1msよりも小さくなっている。
依存性をみるには、.params コマンドで、これらを変数して、変化したときにどうなるかを見てみるとよさそう。
ちなみに、ご本家では、R_in を、
B_THLNK I+ I- I = v(I+,I-) * G
として、電流源で表現していて、ノイズを入れるためである。ここでは最も簡単なものを目指して、抵抗で表現することにした。
X線の熱入力
X線の熱入力はどうやっているかというと、
Iphoton 0 Pout PULSE(0 960p 1m 0 0 1u) ; X線の入力源としての電流パルス
である。ご本家に従い、960pA x 1us = 9.6 x 10^-16 A/s で、9.6x10^-16 W (=6keV)に相当する、という算段より、その通りに踏襲している。
電熱フィードバック
電熱フィードバックのメインは、
B_tes COM TES- I = V(TES+,TES-) / (R0 + A * R0/T * V(Pout)) ; TESの電流
B_power 11 0 V = I(V_0) * v(COM,TES-) ; TESのジュール発熱に相当する電圧を出力
の部分です。B_tes が、
I = \frac{V}{R_0 + \Delta R } = \frac{V}{R_0 + A (R_0/T) \Delta T } = \frac{V}{R_0 + A \frac{R_0}{T} V(Pout)}
としています。抵抗値の変化dRの部分をもう少し具体的に書き下すと、
\Delta R = \frac{d(logR)}{d(logT)} = \frac{dR}{dT}\Delta T = A \frac{R}{T}\Delta T
となり、線形な変化を仮定したことに対応している。Aは温度計感度の所謂アルファ $\alpha$ のことです。V(Pout)がdTに相当します。
温度計感度 $\alpha$ は、
.params R0=50m A=150 T=0.10; R0=動作抵抗、A=温度計感度(所謂アルファ)、T=動作温度
の部分で、150に設定している。TはTESの温度で100mKに設定している。
TESの抵抗が増えた分、電流が減って、ジュール発熱が下がった分は、
B_power 11 0 V = I(V_0) * v(COM,TES-) ; TESのジュール発熱に相当する電圧を出力
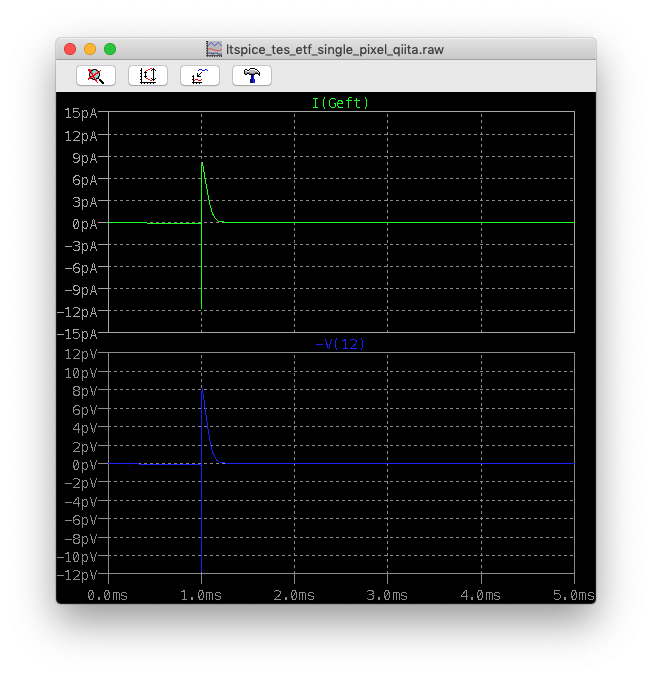
として、電流源(B_power)の分だけ、電流を熱回路から引き出している。これを確認してみよう。プローブするのは、I(Geft)とV(12)である。
横軸縦軸の範囲を完璧に同じにしている。V(12)の電圧を1.0倍した電流(Geft)が流れていることがわかる。これが、フィードバックにより、X線光で熱せられたTESが、ジュール熱が減ることが、EFTがない場合よりも早く冷える(=早く電流がGNDに流れる)ことに対応している。
RC high pass filter
これは、ETFとして入力するためのB_powerの中に定常的な成分が含まれているため、ACだけを取り出すためにいれている。カットオフ周波数は 10F x 10Ω = 100 [sec]で、それよりも遅い変動はGNDに流れて落とされて、AC成分だけが、Geft に入力されている。
Ccut 11 12 10 ; CR high pass filter の C 10F
Rcut 12 0 10 ; CR high pass filter の C 10Ω
Spice関係の補足
温度設定
シミュレーション時に設定した温度 temp と通常温度 tnom がある。この差が dt であり、これらは LTspice の中では事前に定義されている変数である。
params or param
サブサーキットの呼び出し行や、サブサーキットの定義の箇所は"param"ではなく、"params"と"s"が必要になる。他はどちらでも動作する。
結果のplot
saveコマンドは、.save の後に選択した部分だけを保存することで、メモリを削減できる。最近はLTspiceの出力ファイルをpythonで簡単に読めるツール (https://pypi.org/project/ltspice/) があるようだが、、
これはmac版のLTspiceでは、コマンドラインからテキストに書くだす方法がよくわからない(誰かご存知でしたら教えて欲しい)。
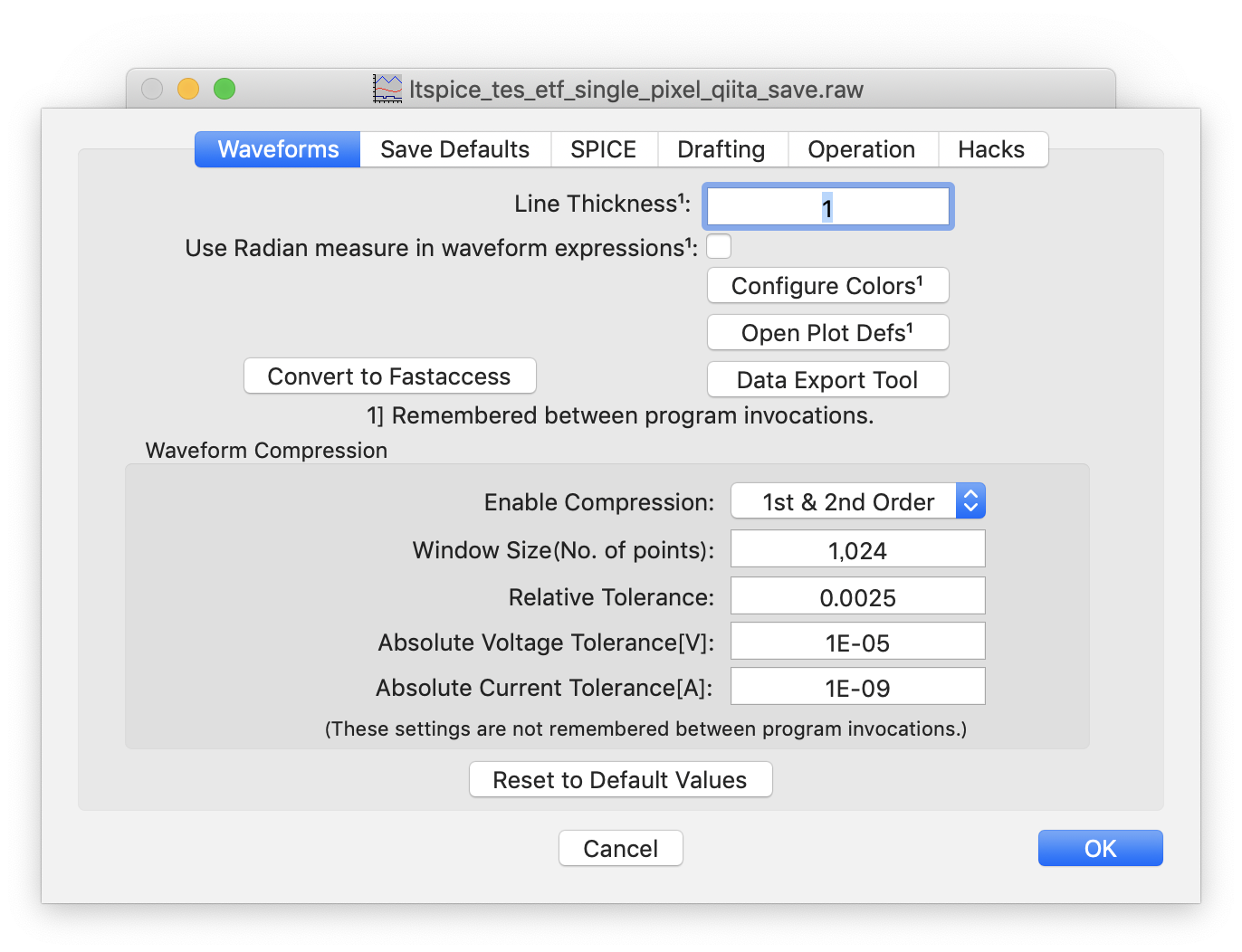
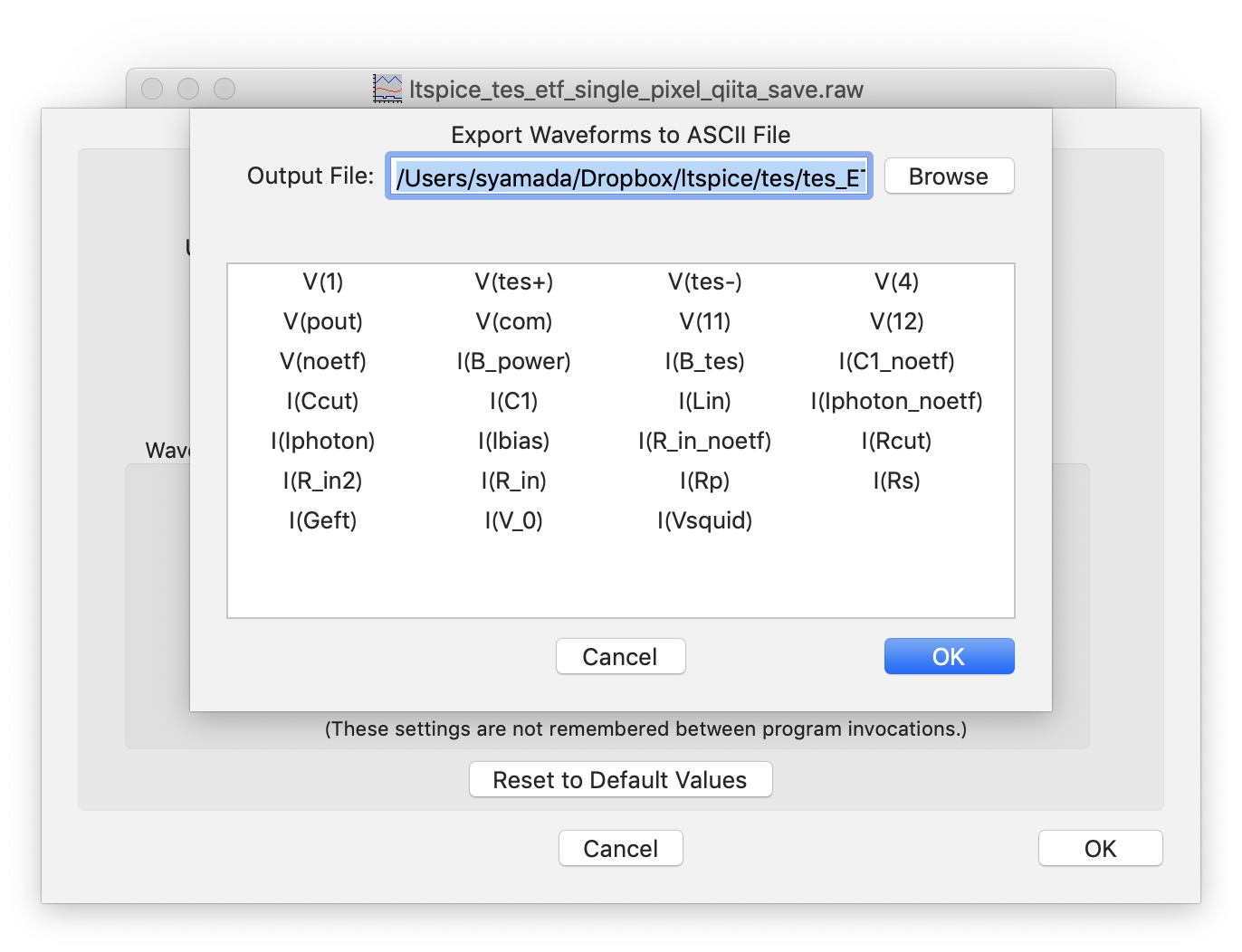
Data Export Tool を押すと、
選択画面が現れるので、必要なデータを選択して、テキストファイルに書き出すことができる。
例えば、V(pout) V(noetf) I(Lin) だけテキストファイルに保存したとして、
簡単にプロットすると、
%head -5 ltspice_tes_etf_single_pixel_qiita_save_960p.txt
time V(pout) V(noetf) I(Lin)
0.000000000000000e+00 1.538920e-13 0.000000e+00 1.754386e-05
1.000034987016229e-03 7.198057e-06 7.195185e-06 1.754304e-05
1.000080261230604e-03 3.902850e-05 3.901193e-05 1.753958e-05
1.000125535444978e-03 7.374024e-05 7.366282e-05 1.752188e-05
....
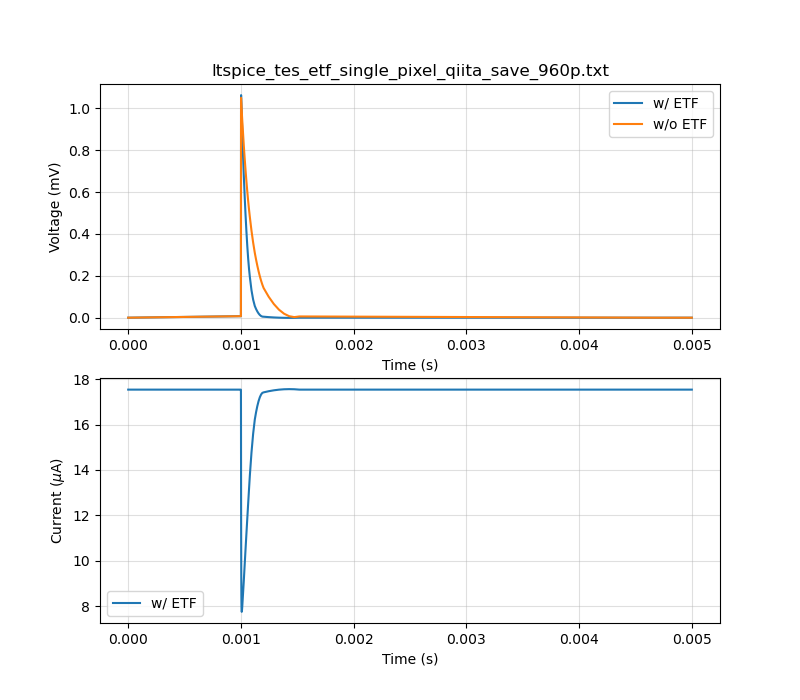
%python plot_ltspice_tes.py ltspice_tes_etf_single_pixel_qiita_save_960p.txt
とすると、
のようにプロットができる。
用いたコードはこちらです。
# !/usr/bin/env python
import os
import sys
import math
argvs = sys.argv
argc = len(argvs)
if (argc != 2):
print ('\n[ERROR] Usage: # python %s file\n' % argvs[0] )
quit()
import numpy as np
import matplotlib.pyplot as plt
fname=argvs[1]
ftag=fname.replace(".txt","")
file = open(fname)
time = []
v_etf = []
v_noetf = []
i_tes = []
for i,one in enumerate(file):
one = one.strip().split()
if i == 0:
print("skip header", one)
continue
time.append(float(one[0]))
v_etf.append(float(one[1]))
v_noetf.append(float(one[2]))
i_tes.append(float(one[3]))
time = np.array(time)
v_etf = np.array(v_etf)
v_noetf = np.array(v_noetf)
i_tes = np.array(i_tes)
F = plt.figure(figsize=(8,7))
ax = plt.subplot(2,1,1)
plt.title(fname)
plt.ylabel("Voltage (mV)")
plt.xlabel('Time (s)')
plt.grid(True,alpha=0.4)
plt.xscale('linear')
plt.yscale('linear')
plt.plot(time,v_etf*1e3,label="w/ ETF")
plt.plot(time,v_noetf*1e3,label="w/o ETF")
plt.legend()
ax = plt.subplot(2,1,2)
plt.ylabel(r"Current ($\mu$A)")
plt.xlabel('Time (s)')
plt.grid(True,alpha=0.4)
plt.xscale('linear')
plt.yscale('linear')
plt.plot(time,i_tes*1e6,label="w/ ETF")
plt.legend()
plt.savefig(ftag+".png")