指数分布とポアソン分布の関係を数式で確認
はじめに
確率論や統計学を学ぶ上で、指数分布とポアソン分布は非常に重要な役割を果たします。特に待ち時間分布や到着イベントのモデル化に使われるこれらの分布は、特定の条件下で密接な関係を持っています。本記事では、この関係を数学的に証明し、具体例を用いて理解を深めたいと思います。
応用例については、
で紹介しています。
基本概念の定義
確率密度関数(PDF)
確率密度関数(Probability Density Function, PDF)は、連続確率変数の値が特定の範囲にある確率を記述する関数です。PDF $ f(x) $ は次の条件を満たします:
- $ f(x) \geq 0 $ for all $ x $
- $ \int_{-\infty}^{\infty} f(x) dx = 1 $
$f(x)$ が 1 以下の無次元量である必要がないことを注意してください。$f(x) dx$で、無次元になればよく、全積分で1になればよいです。
確率質量関数(PMF)
確率質量関数(Probability Mass Function, PMF)は、離散確率変数が特定の値をとる確率を記述する関数です。PMF $ P(X = k) $ は次の条件を満たします:
- $ 0 \leq P(X = k) \leq 1 $ for all $ k $
- $ \sum_{k} P(X = k) = 1 $
ポアソン分布は、整数の数やカウントに対して用いるので、こちらで定義される分布です。
指数分布とは?
定義
指数分布は、ある特定のイベントが次に発生するまでの時間をモデル化します。例えば、電話がかかってくるまでの時間や、不安定同位体など放射性物質の崩壊までの時間などです。
確率密度関数(PDF)は次のように定義されます:
f(x; \lambda) = \lambda e^{-\lambda x}
ここで、$ \lambda $ はイベントの発生率(単位時間あたりの平均発生回数)を表し、$x$は非負の実数で、$ \lambda x$ で無次元になるので、$ \lambda $が1秒あたりであれば $x$ の単位は秒になります。$f(x; \lambda)$ は、$ \lambda $ と同じ次元になるので、無次元ではないわけですが、$dx$ で積分した時に無次元の1という数になるので、$f(x; \lambda)$が無次元でなくても問題ないです。
指数関数はテイラー展開で冪函数に展開すると指数関数の肩の変数の冪乗が出てくるので、無次元以外では次元がおかしくなるので、指数関数の型の数は無次元になります。
累積分布関数(CDF)
累積分布関数 $ F(x) $ は次のように表されます:
F(x) = P(X \leq x) = 1 - e^{-\lambda x}
(例えば、X線が物質中で吸収される確率が $1 - e^{-\tau}$ で、透過する確率が $e^{-\tau}$ であることと同じ話です。)
ポアソン分布とは?
定義
ポアソン分布は、ある時間内に発生する特定のイベントの回数をモデル化します。例えば、1時間あたりの電話の本数や1年あたりの交通事故の数、1秒あたりのX線の数などです。
確率質量関数(PMF)は次のように定義されます:
P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}
ここで、$ \lambda $ は平均発生回数を表します。
指数分布とポアソン分布の関係
ポアソン過程と指数分布
ポアソン過程は、独立したランダムなイベントが発生する過程を指し、この過程での到着時間(待ち時間)間隔は指数分布に従います。具体的には、以下のような関係があります:
(1) イベントの発生回数 $ N(t) $ はポアソン分布に従う:
P(N(t) = k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!}
(2) イベント間の待ち時間 $ T $ は指数分布に従う:
f_T(t) = \lambda e^{-\lambda t}
数学的証明
イベント間の待ち時間が指数分布に従うことの証明
ポアソン過程において、時間 $ t $ 内にイベントが1つも発生しない確率 $ P(N(t) = 0) $ は次のように表されます:
P(N(t) = 0) = e^{-\lambda t}
これは、待ち時間 $ T $ が $ t $ より大きい確率に等しいです:
P(T > t) = e^{-\lambda t}
よって、累積分布関数(CDF)は:
F_T(t) = 1 - e^{-\lambda t}
確率密度関数(PDF)は:
f_T(t) = \frac{d}{dt}F_T(t) = \lambda e^{-\lambda t}
従って、待ち時間 $ T $ は指数分布に従います。
ここで、$\lambda t$ が無次元であれば、どのような物理現象でも同じなので、$l$ が単位長さあたりにエネルギー損失が発生する長さで、$x$を長さとして、$lx$ という量を用いることもできます。
あるイベントが k 回起こるまでの待ち時間の分布
各 $ T_i $ が独立かつ同一の指数分布に従う場合、これらの合計 $ T_1 + T_2 + \cdots + T_k $ はパラメータ $ \lambda $ と形状パラメータ $ k $ を持つガンマ分布に従います。
なぜガンマ分布に従うのか?
ガンマ分布の基本的な概念
ガンマ分布は、待ち時間や時間間隔の合計をモデル化するために使用されます。特に、複数の独立した指数分布に従う待ち時間の合計はガンマ分布に従います。
ガンマ分布の確率密度関数(PDF)は以下のように定義されます:
f(t; k, \lambda) = \frac{\lambda^k t^{k-1} e^{-\lambda t}}{\Gamma(k)}
ここで、
- $ \lambda $ はレートパラメータ
- $ k $ は形状パラメータ(しばしば正の整数)
- $ \Gamma(k) $ はガンマ関数 ($k$が自然数の場合は階乗)
ガンマ分布の確率密度関数を $ k-1 $ を $ n $ として書き直すと、次のようになります:
f(t; n+1, \lambda) = \frac{\lambda (\lambda t)^n e^{-\lambda t}}{n!}
この式は、ポアソン分布の確率質量関数の形状と相似形であり、ポアソン分布の形状が連続分布であるガンマ分布に自然に拡張されることを示しています。ただし、ポアソン分布は自然数$k$に対して定義され、離散的な数による足し算の総和が1になるように規格化されるのに対して、ガンマ分布は連続変数の積分値が1になるように規格化される点が異なります。(どちらも、$f_n(x) = x^n e^{-x} / n! \propto x^n e^{-x}$ という形状で扱いやすいのかな、というくらいの意味です。)
指数分布の合計とガンマ分布
指数分布の特性
指数分布は次の確率密度関数を持ちます:
f_T(t) = \lambda e^{-\lambda t}
この分布の特性として、メモリレス性があります。つまり、ある時点での待ち時間が過ぎても、その後の待ち時間は元の分布に従います。この特性が重要であり、合計がガンマ分布に従う理由の一部となります。
合計の分布
各 $ T_i $ が独立かつ同一の指数分布 $ \lambda $ に従うと仮定します。つまり、
T_i \sim \text{Exponential}(\lambda)
このとき、 $ k $ 個の独立な指数分布に従う変数の合計、
S_k = T_1 + T_2 + \cdots + T_k
の分布がどうなるかを考えます。
ラプラス変換の利用
指数分布の確率密度関数のラプラス変換は、次のようになります:
\mathcal{L}\{f_T(t)\} = \int_0^\infty e^{-st} \lambda e^{-\lambda t} \, dt = \frac{\lambda}{s + \lambda}
次に、複数の独立した指数分布に従う変数の和を考えます。
独立なランダム変数のラプラス変換の性質によると、独立なランダム変数の和のラプラス変換は、それぞれのランダム変数のラプラス変換の積に等しくなります。つまり、もし $ T_1, T_2, \ldots, T_k $ が独立であり、各 $ T_i $ が同じ指数分布 $ f_T(t) = \lambda e^{-\lambda t} $ に従うならば、和 $ S_k = T_1 + T_2 + \cdots + T_k $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{S_k}(t)\} = \mathcal{L}\{f_{T_1}(t)\} \cdot \mathcal{L}\{f_{T_2}(t)\} \cdot \ldots \cdot \mathcal{L}\{f_{T_k}(t)\}
ここで、各 $ T_i $ のラプラス変換は同じ $ \frac{\lambda}{s + \lambda} $ なので、
\mathcal{L}\{f_{S_k}(t)\} = \left( \frac{\lambda}{s + \lambda} \right)^k
となります。
なぜ、ラプラス変換を使うのか?と思った人は、ラプラス変換の畳み込み計算についての詳細な説明 を一読ください。
逆ラプラス変換とガンマ分布
逆ラプラス変換を行うと、次のような結果が得られます:
\mathcal{L}^{-1} \left\{ \frac{\lambda^k}{(s + \lambda)^k} \right\} = \frac{\lambda^k t^{k-1} e^{-\lambda t}}{\Gamma(k)}
これは、ガンマ分布の確率密度関数そのものです。
ポアソン分布とガンマ分布の累積分布関数の関係
ガンマ分布の累積分布関数 $ F_{T_{(k)}}(t) $ は、不完全ガンマ関数 $ \gamma(k, \lambda t) $ を用いて
次のように表されます:
F_{T_{(k)}}(t) = \frac{\gamma(k, \lambda t)}{\Gamma(k)} = \frac{\int_0^{\lambda t} y^{k-1} e^{-y} \, dy}{(k-1)!}
次に、ポアソン分布とガンマ分布の累積分布関数(CDF)の関係を示します。
ポアソン分布における確率
ポアソン分布において、時間 $ t $ 内に $ k $ 回のイベントが発生する確率は次のように定義されます:
P(N(t) = k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!}
ガンマ分布との比較
ガンマ分布の累積分布関数(CDF)は、ある時間 $ t $ 内に $ k $ 回のイベントが発生するまでの総待ち時間の分布を表します。ガンマ分布の形状パラメータ $ k $ とレートパラメータ $ \lambda $ を用いると、次のような関係が成立します:
P(T_1 + T_2 + \cdots + T_k \leq t) = F_{T_{(k)}}(t)
ここで、
F_{T_{(k)}}(t) = \frac{\gamma(k, \lambda t)}{\Gamma(k)}
この式は、ガンマ分布の累積分布関数 $ F_{T_{(k)}}(t) $ を示しており、不完全ガンマ関数 $ \gamma(k, \lambda t) $ を用いています。
ポアソン分布とガンマ分布の繋がりの説明
ポアソン過程の性質に基づいています。ポアソン過程におけるイベントの発生は独立であり、各イベント間の待ち時間は指数分布に従います。複数の独立な指数分布に従う待ち時間の合計はガンマ分布に従うため、時間 $ t $ 内に $ k $ 回のイベントが発生する確率(ポアソン分布)と、$ k $ 回のイベントが発生するまでの総待ち時間が時間 $ t $ 以下である確率(ガンマ分布)は同じ現象を異なる視点で表現しています。
共役事前分布の関係
ベイズ推論において、ポアソン分布の尤度関数とガンマ分布の事前分布の組み合わせは共役性を持ち、事後分布もガンマ分布の形を維持します。具体的には、観測データ $ x_1, x_2, \ldots, x_n $ がポアソン分布に従う場合、尤度関数は次のようになります:
L(\lambda \mid x_1, x_2, \ldots, x_n) = \prod_{i=1}^n \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} = \lambda^{\sum_{i=1}^n x_i} e^{-n\lambda}
事前分布としてガンマ分布を使用すると、事後分布は次のように求められます:
p(\lambda \mid x_1, x_2, \ldots, x_n) \propto L(\lambda \mid x_1, x_2, \ldots, x_n) \cdot p(\lambda)
\propto \lambda^{\sum_{i=1}^n x_i} e^{-n\lambda} \cdot \lambda^{\alpha-1} e^{-\beta \lambda}
\propto \lambda^{\alpha + \sum_{i=1}^n x_i - 1} e^{-(\beta + n)\lambda}
したがって、事後分布もガンマ分布になります:
\lambda \mid x_1, x_2, \ldots, x_n \sim \text{Gamma}(\alpha + \sum_{i=1}^n x_i, \beta + n)
このように、ポアソン分布の共役事前分布がガンマ分布であるため、観測データに基づいてレートパラメータ $\lambda$ を更新する際に、事後分布もガンマ分布の形を維持します。
ポアソン分布は離散的な確率質量関数であり、ガンマ分布は連続的な確率密度関数です。そのため、厳密に直接的な一致という表現は適切ではないでしょうが、イベントの発生回数とイベントの到達時間の関係を通じて、ポアソン分布とガンマ分布が繋がっていることが理解できます。
具体例
電話の受信時間
例えば、あるコールセンターで1分あたり平均2回の電話がかかってくるとしましょう。これは、1分あたりの電話の発生率が $\lambda = 2$ [/min]であることを意味します。平均待ち時間は $ \frac{1}{\lambda} = \frac{1}{2} = 0.5 $ 分です。
イベント間の待ち時間
次の電話がかかってくるまでの待ち時間 $T$ は指数分布に従います:
f_T(t) = 2 e^{-2t}
イベントの発生回数
1分間にかかってくる電話の回数 $N(1)$ はポアソン分布に従います:
P(N(1) = k) = \frac{2^k e^{-2}}{k!}
たとえば、1分間に3回電話がかかってくる確率は:
P(N(1) = 3) = \frac{2^3 e^{-2}}{3!} = \frac{8 e^{-2}}{6} \approx 0.180
システムの故障時間
また、あるシステムが1時間あたり平均1回故障するとしましょう。ここでも、1時間あたりの故障率が $\lambda = 1$ です。
イベント間の待ち時間
次の故障までの待ち時間 $T$ は指数分布に従います:
f_T(t) = e^{-t}
つまり、平均待ち時間は1時間です。
複数の故障までの時間
次に、3回故障するまでの時間を考えます。これらの待ち時間の合計はガンマ分布に従います。形状パラメータが3、レートパラメータが1のガンマ分布です:
f(t; 3, 1) = \frac{t^{2} e^{-t}}{2!} = t^{2} e^{-t} / 2
この分布の平均は3時間、分散は3時間です。
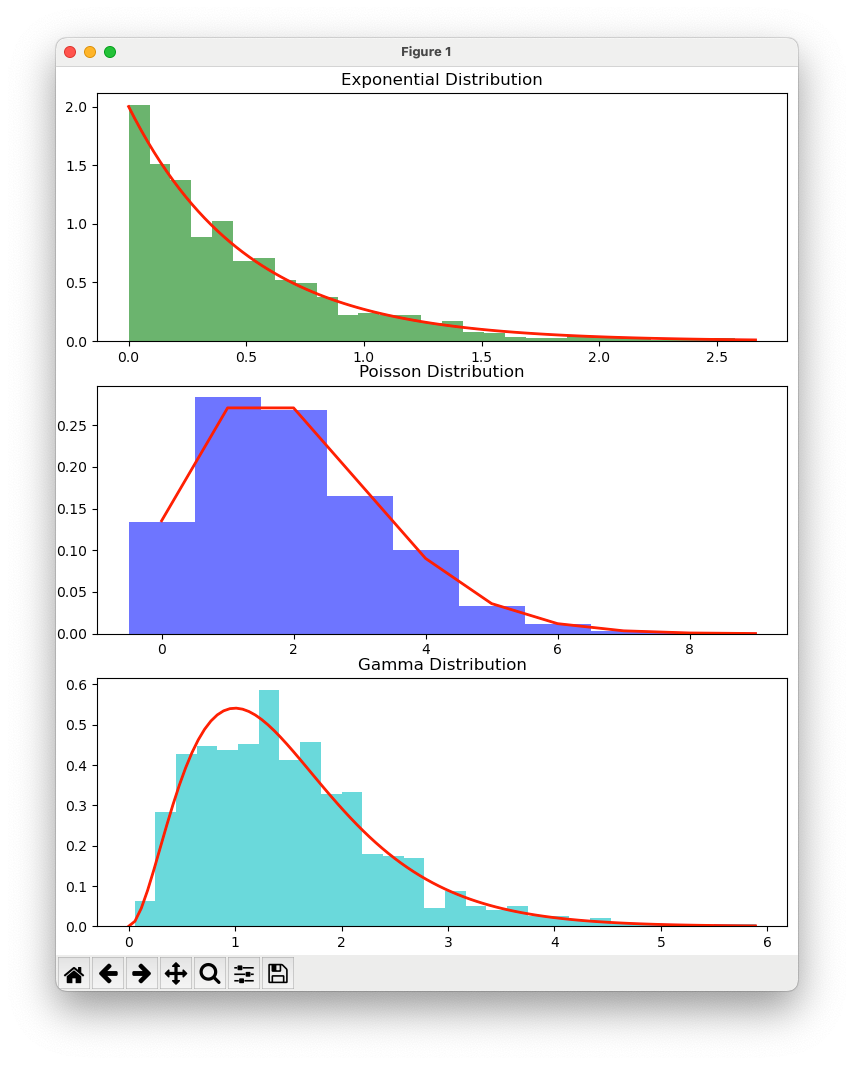
PythonとMatplotlibを用いた簡単な学習例
実際にPythonを使って、指数分布とポアソン分布をシミュレートし、グラフを描いてみましょう。
コード例
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, poisson, gamma
# パラメータ
lambda_val = 2
k_val = 3
# 指数分布のサンプル
expon_samples = expon.rvs(scale=1/lambda_val, size=1000)
# ポアソン分布のサンプル
poisson_samples = poisson.rvs(mu=lambda_val, size=1000)
# ガンマ分布のサンプル
gamma_samples = gamma.rvs(a=k_val, scale=1/lambda_val, size=1000)
# グラフの描画
fig, axs = plt.subplots(3, 1, figsize=(10, 12))
# 指数分布
axs[0].hist(expon_samples, bins=30, density=True, alpha=0.6, color='g')
x = np.linspace(0, np.max(expon_samples), 100)
axs[0].plot(x, expon.pdf(x, scale=1/lambda_val), 'r-', lw=2)
axs[0].set_title('Exponential Distribution')
# ポアソン分布
axs[1].hist(poisson_samples, bins=np.arange(0, np.max(poisson_samples) + 1) - 0.5, density=True, alpha=0.6, color='b')
x = np.arange(0, np.max(poisson_samples) + 1)
axs[1].plot(x, poisson.pmf(x, mu=lambda_val), 'r-', lw=2)
axs[1].set_title('Poisson Distribution')
# ガンマ分布
axs[2].hist(gamma_samples, bins=30, density=True, alpha=0.6, color='c')
x = np.linspace(0, np.max(gamma_samples), 100)
axs[2].plot(x, gamma.pdf(x, a=k_val, scale=1/lambda_val), 'r-', lw=2)
axs[2].set_title('Gamma Distribution')
plt.tight_layout()
plt.show()
コードの説明
-
パラメータ設定:
lambda_valとk_valを設定します。これらは、各分布のパラメータです。 -
サンプル生成:
scipy.statsを使って、指数分布、ポアソン分布、ガンマ分布からサンプルを生成します。 -
ヒストグラム描画:
Matplotlib を使って、各分布のヒストグラムと理論的な確率密度関数(PDF)または確率質量関数(PMF)を描画します。
これにより、指数分布、ポアソン分布、ガンマ分布の特徴とその関係を視覚的に確認することができます。
ラプラス変換の畳み込み計算についての詳細な説明
以下に、時間空間での積分とラプラス変換を用いた畳み込みについて、二つ、三つ、多数の場合それぞれについて具体的に説明します。
独立な指数分布の和の畳み込み
二つの独立な指数分布
時間空間での積分
独立な指数分布 $ T_1 $ と $ T_2 $ があり、それぞれの確率密度関数(PDF)は次のようになります:
f_{T_i}(t) = \lambda e^{-\lambda t}
二つの独立なランダム変数の和 $ S_2 = T_1 + T_2 $ の確率密度関数は、これらの畳み込みで表されます:
f_{S_2}(t) = (f_{T_1} * f_{T_2})(t) = \int_0^t f_{T_1}(\tau) f_{T_2}(t - \tau) \, d\tau
具体的には、
f_{S_2}(t) = \int_0^t \lambda e^{-\lambda \tau} \lambda e^{-\lambda (t - \tau)} \, d\tau
= \lambda^2 e^{-\lambda t} \int_0^t e^{-\lambda \tau} e^{\lambda \tau} \, d\tau
= \lambda^2 e^{-\lambda t} \int_0^t e^{0} \, d\tau
= \lambda^2 e^{-\lambda t} \int_0^t 1 \, d\tau
= \lambda^2 e^{-\lambda t} t
したがって、二つの独立な指数分布の和の PDF は次のようになります:
f_{S_2}(t) = \lambda^2 t e^{-\lambda t}
ラプラス変換を用いた畳み込み
各 $ T_i $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{T_i}(t)\} = \frac{\lambda}{s + \lambda}
二つの独立な指数分布の和 $ S_2 = T_1 + T_2 $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{S_2}(t)\} = \mathcal{L}\{f_{T_1}(t)\} \cdot \mathcal{L}\{f_{T_2}(t)\}
= \left( \frac{\lambda}{s + \lambda} \right) \cdot \left( \frac{\lambda}{s + \lambda} \right)
= \left( \frac{\lambda}{s + \lambda} \right)^2
三つの独立な指数分布
時間空間での積分
次に、三つの独立な指数分布 $ T_1, T_2, T_3 $ の和 $ S_3 = T_1 + T_2 + T_3 $ を考えます。
まず、二つの独立な指数分布の和 $ S_2 = T_1 + T_2 $ の確率密度関数は次のようになります:
次に、三つ目の独立な指数分布 $ T_3 $ との和 $ S_3 = S_2 + T_3 $ を考えます。この場合の畳み込み積分は次のようになります:
f_{S_3}(t) = (f_{S_2} * f_{T_3})(t) = \int_0^t f_{S_2}(\tau) f_{T_3}(t - \tau) \, d\tau
具体的には、
f_{S_3}(t) = \int_0^t \lambda^2 \tau e^{-\lambda \tau} \lambda e^{-\lambda (t - \tau)} \, d\tau
= \lambda^3 e^{-\lambda t} \int_0^t \tau \, d\tau
積分を計算すると、
\int_0^t \tau \, d\tau = \left[ \frac{\tau^2}{2} \right]_0^t = \frac{t^2}{2}
したがって、三つの独立な指数分布の和の PDF は次のようになります:
f_{S_3}(t) = \lambda^3 e^{-\lambda t} \cdot \frac{t^2}{2} = \frac{\lambda^3 t^2 e^{-\lambda t}}{2}
ラプラス変換を用いた畳み込み
まず、二つの独立な指数分布の和 $ S_2 = T_1 + T_2 $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{S_2}(t)\} = \left( \frac{\lambda}{s + \lambda} \right)^2
次に、三つ目の独立な指数分布 $ T_3 $ との和 $ S_3 = S_2 + T_3 $ のラプラス変換を求めます:
\mathcal{L}\{f_{S_3}(t)\} = \mathcal{L}\{f_{S_2}(t)\} \cdot \mathcal{L}\{f_{T_3}(t)\}
= \left( \frac{\lambda}{s + \lambda} \right)^2 \cdot \frac{\lambda}{s + \lambda}
= \left( \frac{\lambda}{s + \lambda} \right)^3
多数の独立な指数分布
時間空間での積分
一般的に、$ k $ 個の独立な指数分布 $ T_1, T_2, \ldots, T_k $ の和 $ S_k = T_1 + T_2 + \cdots + T_k $ の確率密度関数は次のように畳み込みで表されます:
f_{S_k}(t) = (f_{T_1} * f_{T_2} * \cdots * f_{T_k})(t)
この畳み込み積分は次のようになります:
f_{S_k}(t) = \int_0^t f_{S_{k-1}}(\tau) f_{T_k}(t - \tau) \, d\tau
一般に、$ k $ 個の独立な指数分布の和の確率密度関数はガンマ分布の形状に対応し、次のように表されます:
f_{S_k}(t) = \frac{\lambda^k t^{k-1} e^{-\lambda t}}{(k-1)!}
ラプラス変換を用いた畳み込み
ラプラス変換を用いると、各 $ T_i $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{T_i}(t)\} = \frac{\lambda}{s + \lambda}
$ k $ 個の独立な指数分布の和 $ S_k $ のラプラス変換は次のようになります:
\mathcal{L}\{f_{S_k}(t)\} = \mathcal{L}\{f_{T_1}(t)\} \cdot \mathcal{L}\{f_{T_2}(t)\} \cdot \ldots \cdot \mathcal{L}\{f_{T_k}(t)\}
= \left( \frac{\lambda}{s + \lambda} \right) \cdot \left( \frac{\lambda}{s + \lambda} \right) \cdot \ldots \cdot \left( \frac{\lambda}{s + \lambda} \right)
= \left( \frac{\lambda}{s + \lambda} \right)^k
このように、二つ、三つ、多数の独立な指数分布の和について、時間空間での積分とラプラス変換を用いた畳み込みをそれぞれ具体的に計算してみると、どちらで計算しても同じ結果になることがわかると思います。
まとめ
ポアソン分布と指数分布の関係を理解することで、待ち時間や到着イベントのモデル化が容易になります。データ分析や、シミュレーションの設計に役立てば幸いです。