Go to Qiita Advent Calendar 2024 Top
LoginSignup
2
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@yamadasuzaku(Shinya Yamada)in立教大学

太陽組成(宇宙組成)について簡単にまとめてみた

Last updated at Posted at 2022-08-28

太陽組成(宇宙組成)について

我々の宇宙や太陽がどういう組成で出来ているのか、元素ごとの存在比で示した量として太陽組成(宇宙組成) があり、英語では solar abundance や アバンダンス ( Abundance of chemical elements の略) と言われることが多いです。これをある程度は理解して使いたいのですが、意外と奥が深い(私もまだ勉強中というレベル)のと、簡単にプロットしたいときに、源泉情報を探すのが大変なので、ここでまとめておきたいと思います。

太陽組成について簡単な説明

太陽組成(宇宙組成)という言い方をした場合は、太陽光球の分光観測で得られた元素組成を指すだけの時もあれば、隕石(コンドライト)の分析値を合わせて、隕石が太陽系全体の元素存在度（宇宙組成比）をよく近似していると仮定して、太陽組成ということもあります(天文学辞典さんより)。通常は、Siの量を10^6としたときの個数比の相対量で表すことが多いが、質量比の場合もあります。分析手法や評価方法の違いや、作成された時期によって、太陽組成は一意的には決まらないし、まさに最近のリュウグウの結果や、NASAの探査機「オシリス・レックス」も無事に成功すれば、年々更新されていく(?)のではないかと思います。

より詳細には 基礎事項 を最後につけておきました。今後も変化していることを踏まえ、太陽組成はこれです！と出すことだけを目的の一部とはせずに、データの読み方や不定性についても紹介したいと思います。

アバンダンスの定義の注意点

"アバンダンス" という言葉は、微妙に異なる定義で使われることがあるので、注意が必要です。

  • とある太陽組成を仮定して、それとの比。normalized abundance や、ralative abundance などと呼ばれる場合や、abundance とだけ言われる場合がある。
  • 水素を基準にした、元素量として定義される。
  • 水素を基準にした、元素量ではあるが、みやすさのために、log をとって定義されている。Lodders 2003 の 式1で定義されてるように、$log(Fe)/log(He) + 12$ で表示される。

文脈と数字で判断することが必要です。

太陽組成(宇宙組成)のデータとプロット

概略

python が分かる方は、google Colab 上での実演例 を見ていただけばよいかと思います。下記で紹介するコードとデータについては次の通りです。

亜鉛(Zinc Z=30)以下の太陽組成の比較

まずは、"アバンダンス" or 太陽組成といったときに、どの程度の種類があって、どの程度異なるかを見るために、

の比較から紹介します。

NASAの(宇宙)X線スペクトル解析ソフト xspec では、下記の9種類のアバンダンスが用意されています。

冒頭の太字は弁別のための モデルの略称 です。

データの取得

gdown を用いて、google drive 上に置いてある csv ファイルをダウンロードします。


import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import matplotlib.cm as cm
plt.rcParams['font.family'] = 'serif'
parameters = {'axes.labelsize': 15, 'axes.titlesize': 15, 'xtick.labelsize' : 14, 'ytick.labelsize' : 14}
plt.rcParams.update(parameters)

from matplotlib.colors import LogNorm
import matplotlib.colors as colors
import gdown # https://github.com/wkentaro/gdown

# download data
fileURL="https://drive.google.com/file/d/1Xw2rfTC_crSodKGNgGbhvHOX2tEZw7yy/view?usp=sharing" # download solar_xspec_qiita.csv 
localfile="local_solar_xspec_qiita.csv"
gdown.download(fileURL, localfile, quiet=False, fuzzy=True)
data1 = pd.read_csv(localfile)

csv ファイルを、ローカルに保存して、pandas で開いています。必ず、中身が正しく詰まってることは確認しましょう。

アバンダンスのプロット

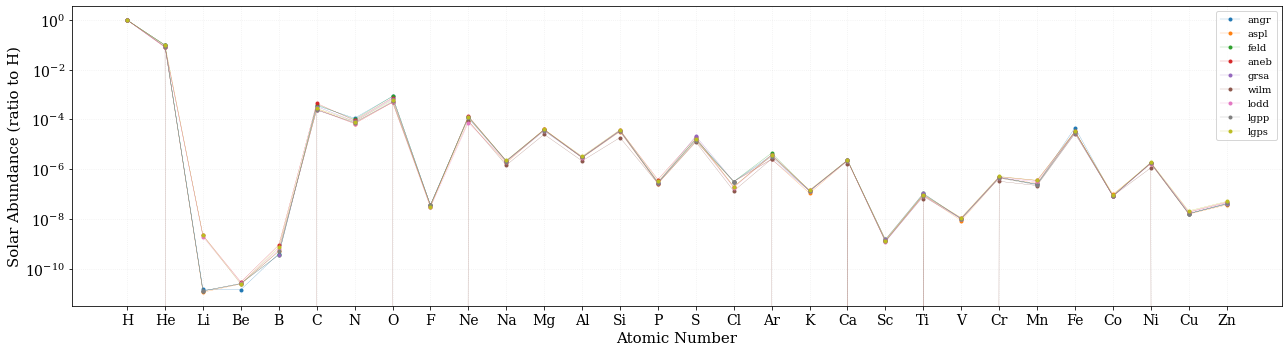
まずは、個数比のプロットを作成します。ここでは xspec の慣例に従って、水素が 1.0 になるように規格化してあります。

# number weighted Solar abundance (used in xspec)
ablist = data1.columns[3:]
fig = plt.figure(figsize =(18, 5))
for ab in ablist:
    plt.plot(data1['Z'], data1[ab],".-",label=ab, lw=0.2)
    plt.xticks(data1['Z'], data1['El'])
    plt.grid(alpha=0.2, ls="dotted")
    plt.yscale("log")
    plt.ylabel("Solar Abundance (ratio to H)")
    plt.xlabel("Atomic Number")
    plt.legend(loc="best")
plt.show()

solar_xspec_raw.png

水素、ヘリウムが多いですね。また、ジグザグした形をしていますね。これは、Oddo Harkins rule と呼ばれるもので、傾向自体は1920年の少し前に発見されたものですが、なぜそうなのか？は量子力学や原子核物理が必要になりますし、全てを基礎物理学だけで説明できるとは限らないです(元素組成量は宇宙創生から138億年後のある場所ある時点での元素量なので、地球物理や宇宙化学の効果も考える必要あります。)。

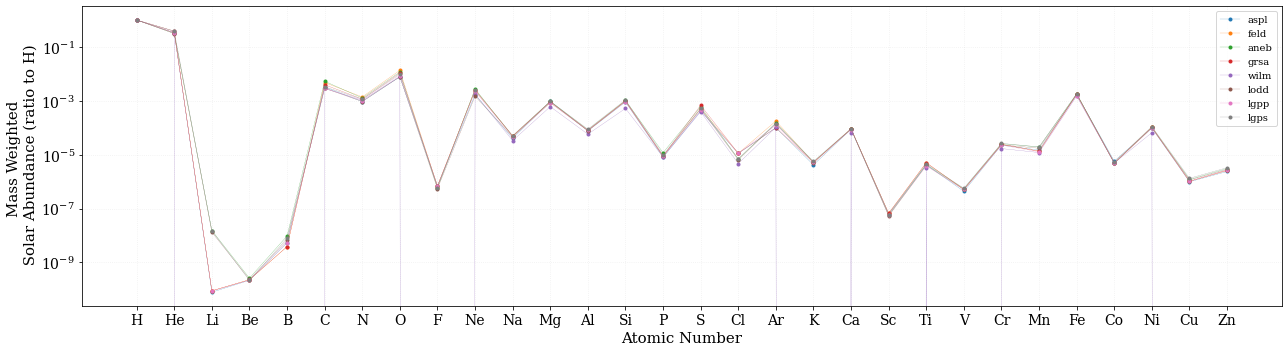
個数比ではなくて、質量比でもみてみましょう。

# mass weighted Solar Abundance (used in xspec)
angrdata = data1[data1.columns[3]] 
ablist = data1.columns[4:]
fig = plt.figure(figsize =(18, 5))
for ab in ablist:
    plt.plot(data1['Z'], data1[ab]*data1['atomicMass'],".-",label=ab, lw=0.2)
    plt.xticks(data1['Z'], data1['El'])
    plt.grid(alpha=0.2, ls="dotted")
    plt.yscale("log")    
    plt.ylabel("Mass Weighted \n Solar Abundance (ratio to H)")
    plt.xlabel("Atomic Number")
    plt.legend(loc="best")
plt.show()

solar_xspec_mass.png

質量で見ると、水素、ヘリウム以外も、そこそこ寄与がありますね。
宇宙では、ヘリウムより重い元素のことを、「金属(メタル)」とか、重元素と呼びます (天文学時点のメタル参照)。ヘリウム以外の元素がたくさん存在していることを、「宇宙は重元素に汚染されてきた」 という言い方もします。

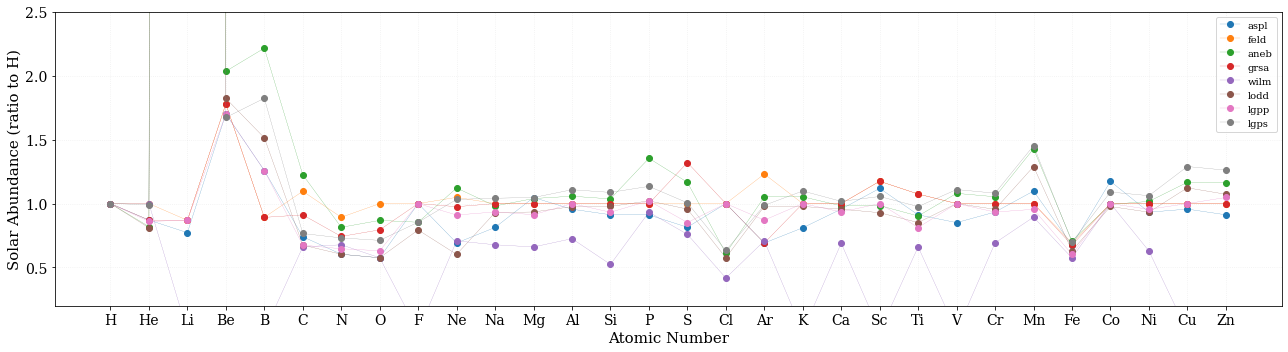
最後に、Anders E. & Grevesse N., 1989 (angr) (xspecのデフォルトの値) で、全体を規格化して、微妙な違いを確認しましょう。

# ratio to Anders E. & Grevesse N., 1989 (angr) (default in xspec)
angrdata = data1[data1.columns[3]] 
ablist = data1.columns[4:]
fig = plt.figure(figsize =(18, 5))
for ab in ablist:
    plt.plot(data1['Z'], data1[ab]/angrdata,"o-",label=ab, lw=0.2)
    plt.xticks(data1['Z'], data1['El'])
    plt.grid(alpha=0.2, ls="dotted")
    plt.ylim(0.2,2.5)
    plt.ylabel("Solar Abundance (ratio to H)")
    plt.xlabel("Atomic Number")
    plt.legend(loc="best")
plt.show()

solar_xspec.png

全体的に20%程度は不定性がある感じですね。Wilmsのデータだけ低めなのは、X線の星間吸収から決めたデータだからだと思います。

Fe/Ni 比についての注意

xspec ではデフォルトで angr を使いますが、これを用いると、Fe/Ni 比が 1.5倍ほど間違えるので注意が必要です。(angrが他のモデルよりもFeが多いためです。)

に実行例をおいてますが、

スクリーンショット 2024-09-06 19.42.26.png

これが Ni/Feの個数比をアバンダンスモデルごとにプロットしたものです。
このように、xspec のデフォルトの angr を使うと、Ni/Feの比が 0.38 であるが、他のモデルでは、0.6 近いので、1.5倍ほど異なることに注意が必要。

Ni/Feを議論する場合は、xspecを使う人は、

XSPEC12>set abund lgps

としてから、定量評価をするとよいでしょう。

太陽組成 (太陽光球とCI隕石の比較)

次に、太陽組成とCI隕石の関係について見てみましょう。元素も、隕石の分析であれば、半減期が約45億年もあるウランも決めることができるので、ウランまでみてみましょう。

データのダウンロード

を手元にダウンロードしましょう。

# download data
# original data : https://iopscience.iop.org/article/10.1086/375492/fulltext/57586.tb1.html?doi=10.1086/375492
# merged data : https://docs.google.com/spreadsheets/d/1uxNPy6nmYbksu01X1LYhYRC1Zfwqew3OWw_2Ajj8_EI/edit?usp=sharing
fileURL="https://drive.google.com/file/d/1Bx3lSXc2Tjk7Vf44eqvF4gvl6XDlpJxB/view?usp=sharing" # download solar_full_qiita.csv 
localfile="local_solar_full_qiita.csv"
gdown.download(fileURL, localfile, quiet=False, fuzzy=True)
data = pd.read_csv(localfile)

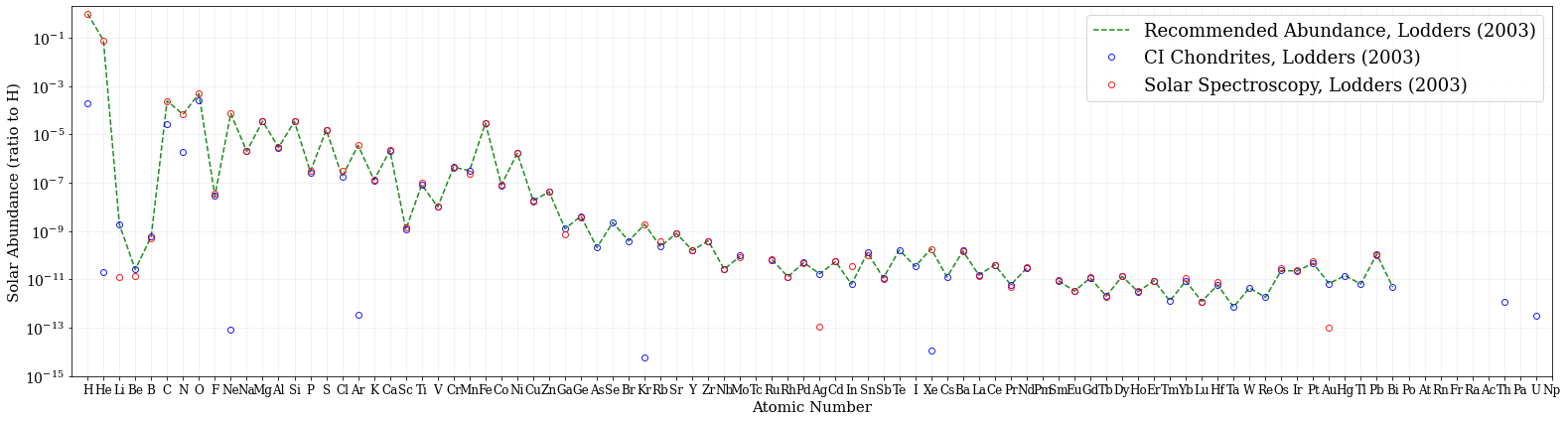
アバンダンス (Lodders 2003)

# mass weighted Solar Abundance
ablist = ['lo2003_H', 'lo2003_CI_H','lo2003_sun_H']
leglist = ['Recommended Abundance, Lodders (2003)','CI Chondrites, Lodders (2003)', 'Solar Spectroscopy, Lodders (2003)']
lablist = ["g--","bo","ro"]
fig = plt.figure(figsize =(22, 6))
for i, (ab,leg,lab) in enumerate(zip(ablist,leglist,lablist)):
    plt.plot(data['Z'], data[ab], lab, label=leg, alpha=0.9, markerfacecolor='none')            
    plt.xticks(data['Z'], data['El'], fontsize=12)    
    plt.grid(alpha=0.2)
    plt.ylim(1e-15,2)
    plt.xlim(0,93) 
    plt.yscale("log")    
    plt.ylabel("Solar Abundance (ratio to H)")
    plt.xlabel("Atomic Number")
    plt.legend(loc="best", fontsize=18)

lo_all.png

隕石は希ガスや揮発性の高いガスは抜けているので、低めに来ています。太陽光球(Solar Spectroscopy)の方は、観測が難しい元素はデータがありません。水素が 1.0 になるように規格化してあります。Recommended Abundance というのは、Lodders (2003) の中で、隕石と太陽観測のデータをよく考えてマージしたようなものです。

凝結温度と元素の関係

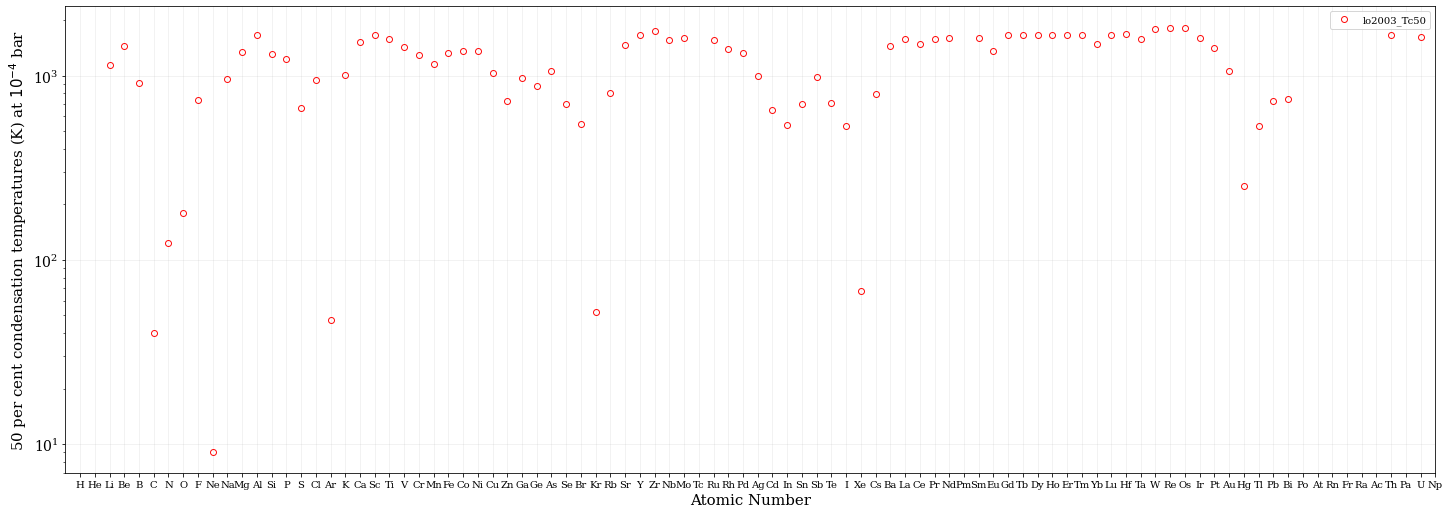
次に、凝結温度(condensation temperature)と、元素の関係を見てみましょう。Tc50 という凝結温度(condensation temperature)は、50%ほど気相と固相or液相に存在している温度のことで、昇華/凝結の切り替わる目安の温度として使われていて、太陽系の始原的なガスが冷却する時にどのような元素から凝結したのかを推定する上で大切な量になります。凝結温度は、Lodders (2003) の値を使っています。

# 50 per cent condensation temperatures (K) at 10^-4 bar
tc='lo2003_Tc50'
fig = plt.figure(figsize =(20, 7))
plt.plot(data['Z'], data[tc],"ro",label=tc,alpha=0.95,markerfacecolor='none')    
plt.xticks(data['Z'], data['El'],fontsize=10)    
plt.grid(alpha=0.2)
plt.xlim(0,93)
plt.yscale("log")    
plt.ylabel(r"50 per cent condensation temperatures (K) at $10^{-4}$ bar")
plt.xlabel("Atomic Number")
plt.legend(loc="best")
plt.tight_layout()

lo_co.png

希ガスといくつかの元素が凝結温度が低いことがわかります。

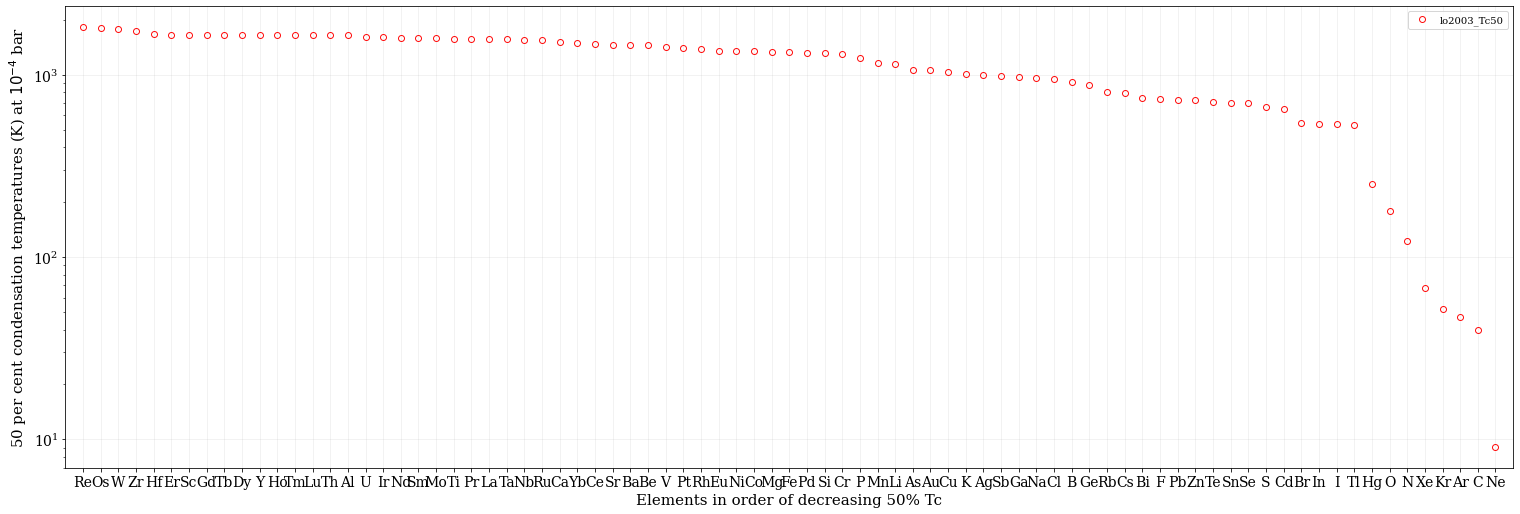
凝結温度の高い順に並び替える

最後に、凝結温度の高い順にデータを並び替えてみましょう。

# (sorted) 50 per cent condensation temperatures (K) at 10^-4 bar
tc='lo2003_Tc50'
cutdata = data.dropna(subset=[tc]).sort_values(tc,ascending=False) # 凝結温度で降順で並び替えて、NaNをカットする。

fig = plt.figure(figsize =(21,7))
plt.plot(cutdata['El'], cutdata[tc],"ro",label=tc,alpha=0.95,markerfacecolor='none')    
plt.grid(alpha=0.2)
plt.xlim(-1,len(cutdata['El']))
plt.yscale("log")    
plt.ylabel(r"50 per cent condensation temperatures (K) at $10^{-4}$ bar")
plt.xlabel("Elements in order of decreasing 50% Tc")
plt.legend(loc="best")
plt.tight_layout()

lo_co2.png

簡単に並び替えられましたね。dropna(subset=[tc]) で NaN のデータをカットして、sort_values(tc,ascending=False) でソートをしています。

炭素質コンドライト隕石の元素組成の比較

データのダウンロード

炭素質コンドライト隕石のデータは、下記を用いています。

# download data
# original data : https://www.sciencedirect.com/science/article/pii/S0016703718304095#t0010
# merged data : https://docs.google.com/spreadsheets/d/1uxNPy6nmYbksu01X1LYhYRC1Zfwqew3OWw_2Ajj8_EI/edit#gid=1868334133
fileURL="https://drive.google.com/file/d/1GGUa_r9SmOXlctOXwyW8ovFqnnFRWR1X/view?usp=sharing" # download solar_full_qiita.csv 
localfile="local_solar_full_qiita.csv"
gdown.download(fileURL, localfile, quiet=False, fuzzy=True)
data3 = pd.read_csv(localfile)

データが多いので、Ivuna 隕石のデータで NaNをカットして、Tc50で降順でソートしておきましょう。

sortname='Ivuna_CI1'
tc='lo2003_Tc50'
cutdata3 = data3.dropna(subset=[sortname]).sort_values(tc,ascending=False)

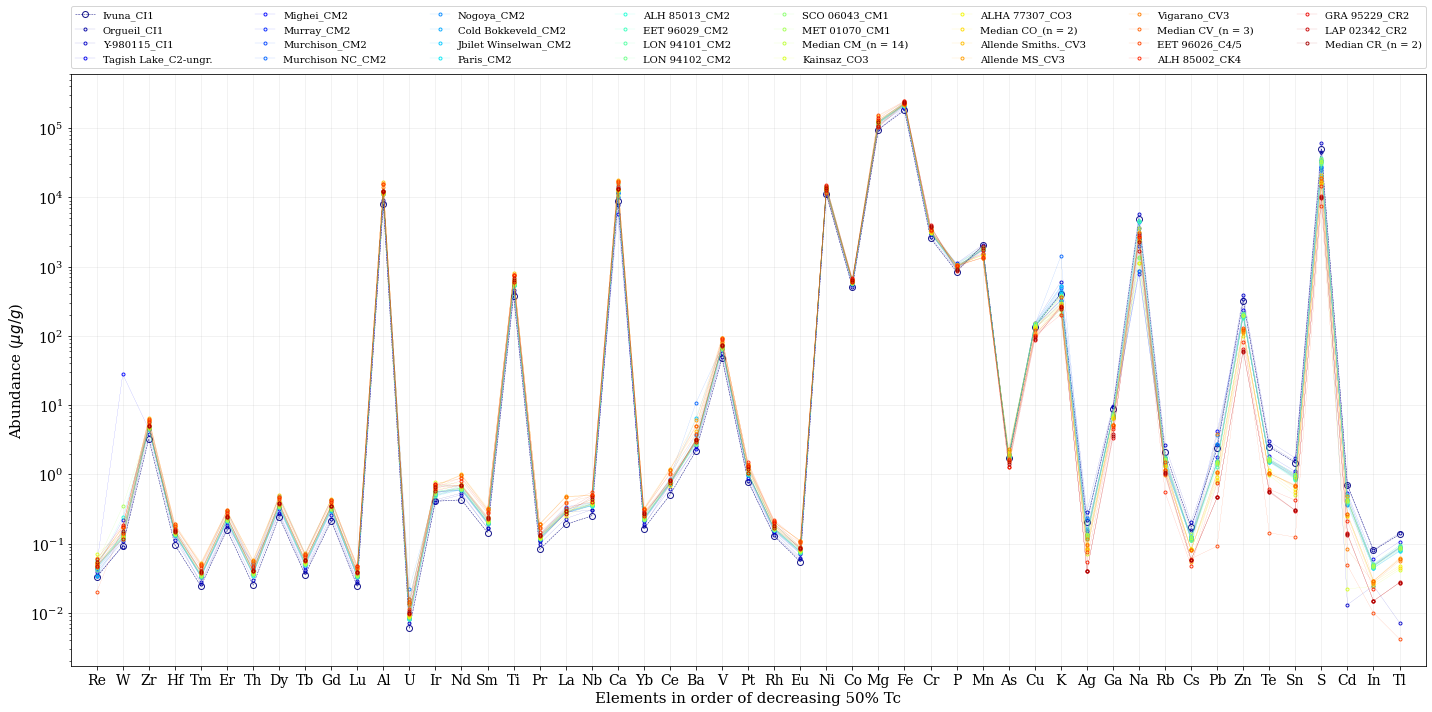
アバンダンスのプロット (CI隕石の比較)

# Abundance ($\mu g/g$) 
ablist = cutdata3.columns[4:]
fig = plt.figure(figsize =(20, 10))

num=len(ablist)
usercmap = plt.get_cmap('jet')
cNorm  = colors.Normalize(vmin=0, vmax=num)
scalarMap = cm.ScalarMappable(norm=cNorm, cmap=usercmap)

parameters = {'axes.labelsize': 15,
              'axes.titlesize': 15,
              'xtick.labelsize' : 14, 
              'ytick.labelsize' : 14}
plt.rcParams.update(parameters)

for i, ab in enumerate(ablist):
    c = scalarMap.to_rgba(i)
    if i == 0:
        plt.plot(cutdata3['El'], cutdata3[ab], "o--",label=ab,alpha=0.9,markerfacecolor='none', color=c, lw=0.5)            
    else:
        plt.plot(cutdata3['El'], cutdata3[ab], ".-",label=ab,alpha=0.9,markerfacecolor='none', color=c, lw=0.1)                    
#    plt.xticks(cutdata3['Z'], cutdata3['El'])    
    plt.tight_layout()
    plt.grid(alpha=0.2)
#    plt.ylim(1e-15,2)
    plt.xlim(-1,len(cutdata3['El']))
    plt.yscale("log")    
    plt.ylabel(r"Abundance ($\mu g/g$)") #  obtained by SF-ICP-MS
    plt.xlabel("Elements in order of decreasing 50% Tc")
    plt.legend(bbox_to_anchor=(0., 1.01, 1., 0.01), loc='lower left',ncol=8, mode="expand", borderaxespad=0.,fontsize=10)
    
plt.show()

man_1.png

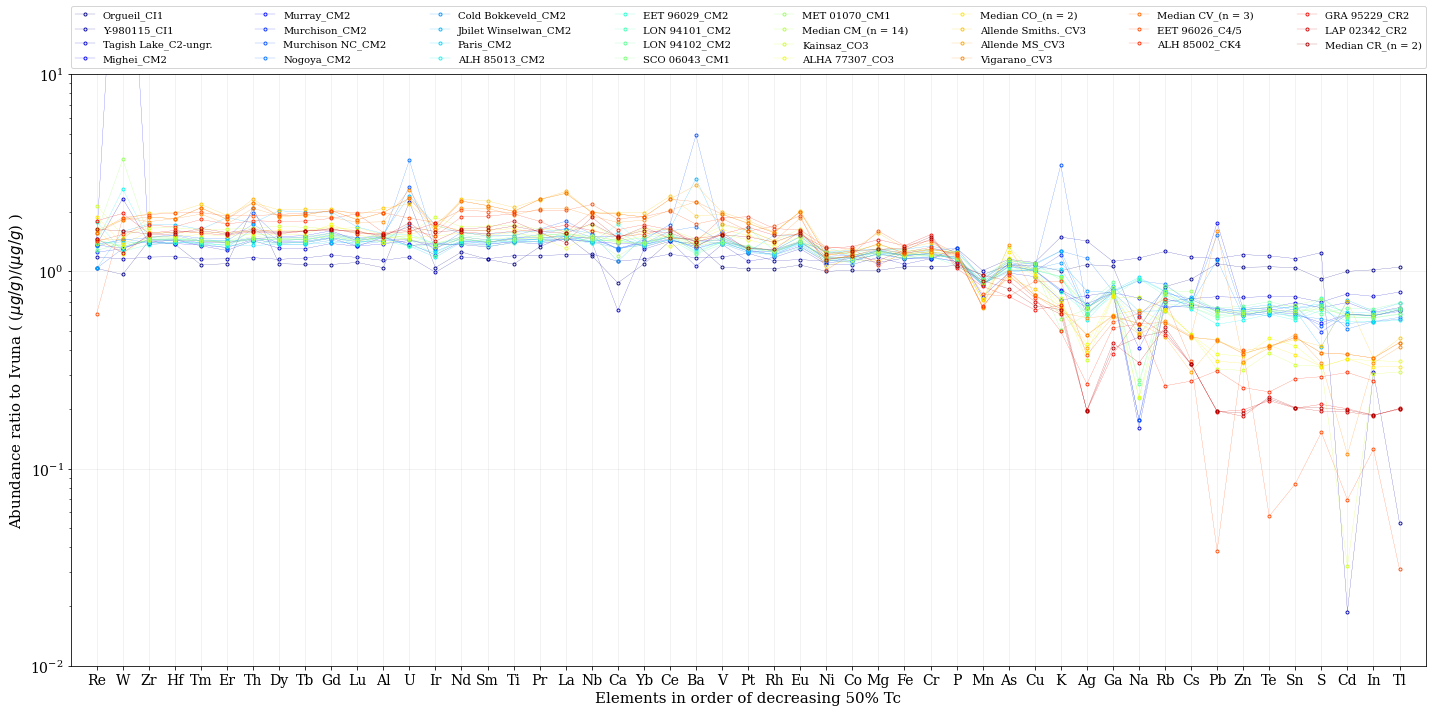
何桁にもわたる縦軸のスケールでは、だいたい同じにみえますね。次に、Ivuna のデータで他を割り算して、違いを見てみましょう。

# Ivuna のデータとの割り算で規格化したアバンダンス
Ivuna = cutdata3['Ivuna_CI1']
ablist = cutdata3.columns[5:]
fig = plt.figure(figsize =(20, 10))

num=len(ablist)
usercmap = plt.get_cmap('jet')
cNorm  = colors.Normalize(vmin=0, vmax=num)
scalarMap = cm.ScalarMappable(norm=cNorm, cmap=usercmap)

for i, ab in enumerate(ablist):
    c = scalarMap.to_rgba(i)
    plt.plot(cutdata3['El'], cutdata3[ab]/Ivuna, ".-",label=ab,alpha=0.9,markerfacecolor='none', color=c, lw=0.2)                    
#    plt.xticks(cutdata3['Z'], cutdata3['El'])    
    plt.grid(alpha=0.2)
    plt.ylim(0.01,10)
    plt.xlim(-1,len(cutdata3['El']))
    plt.yscale("log")    
    plt.ylabel(r"Abundance ratio to Ivuna ( ($\mu g/g$)/($\mu g/g$) )") #  obtained by SF-ICP-MS
    plt.xlabel("Elements in order of decreasing 50% Tc")
    plt.legend(bbox_to_anchor=(0., 1.01, 1., 0.01), loc='lower left',ncol=8, mode="expand", borderaxespad=0.,fontsize=10)

plt.tight_layout()    
plt.show()

man_2.png

Ivuna 隕石のデータとの比をとったもの。凝結温度が低い（右側）ほど、ばらつきが大きく見える。詳細は、原論文 を参考ください。

線の色を連続的に変える方法は、下記に書いています。

このあたりでソフトウェアの練習として必要なものは揃ったのではないでしょうか。

おまけの背景知識

基礎事項

いくつか背景知識や単語を知っておくと良さそうなことを列記しておきます。

  • なぜ太陽と隕石が関係あるの？ 宇宙組成？？

    • (ざっくりとした説明) 太陽は始原的(太陽系生成前の環境)な元素分布を保持していると考えていて、隕石の中でも始原的な隕石は太陽系形成時のタイムカプセルのようにその時の元素分布を保持していると考えると、両者には近い関係が期待できます。太陽系の素は何か？というと、宇宙が137億年前にビックバンで生成して、太陽系ができたのが45億年前なので、多くの星が一生を終えて、様々な元素が散りばめられ混ざった状態から太陽が生まれたと考えられているため、宇宙の平均的な組成は太陽組成に近いと考えられます。
    • 太陽組成とは太陽のどこ？?45億年も変化しないの?という話などは、太陽の化学組成に関する 最近の話題 竹田洋一先生 (国立天文台) をご参照ください。
    • 海老原先生 元素の太陽系存在度と地球存在度 の記事など参考。Anders & Ebihara 1982の海老原先生です。 他にも、[第１回 Oddo-Harkins（オド-ハーキンス）の法則 (太田充恒氏) ] (https://staff.aist.go.jp/a.ohta/japanese/study/REE_ex_es1.htm) など、このページよりも良いものはたくさんあります。。
    • 宇宙組成については、銀河団ガスも太陽と同じ化学組成など、進化した銀河団では太陽組成に近いようです。(ただし、上記は全元素ではなくて、Si, S, Ar, Ca, Cr, Mn, Ni についての測定結果です。また、星による元素合成が起こる前の初期宇宙では元素組成は大きく異なります。)

  • refractory

    • 宇宙化学では「難揮発性」の意味で、 とくに星雲が冷えてゆくときに最初に凝縮する元素のことを指すこともある。対義語は volatile 「揮発性」
    • refractory <=> volatility が宇宙化学では大切。(それぞれ、一般的な用語では、非可燃性、株価変動、という意味で使われるので注意)

  • 地球の内部

    • 力学的区分として、地上から順に、「リソノスフェア(プレート)」「アセノスフェア」「メソスフェア」と呼ばれます。(「理想の飴(リソうのアメ)」などで覚えておきましょう。)
    • 謎解き地震学 さんなど参考。他にも、マントルの大部分を占めるカンラン石（かんらんせき、橄欖石、olivine、オリビン）、カンラン岩（peridotite）など、鉱物や岩石の固有名詞や、宇宙化学、地球惑星の背景があるとベターでしょう。

  • 凝縮

    • 気体が固体になること。英語は、condensation です。 宇宙は高真空なので、星形成時は気体から固体に相転移するので、凝縮がしばしば登場します。
    • 「昇華」の逆は「凝華」 という記事ありました。凝縮は、昇華(sublimation)の逆のプロセスを意味します。

  • 安定同位体や放射性同位体など

    • なぜ45億年前に太陽が誕生したのか？を放射性同位体から知ることができます。宇宙での元素合成は爆発的元素合成と呼ばれ、星の爆発や中性子星同士の合体など、短時間の爆発で生成されます。そのため、生成された元素の中には、不安定な原子核の状態で生まれ、何億年もかけて崩壊するものもあります。
    • 一概に元素比といっても、単核種元素と呼ばれる安定同位体が実質一つしかない元素から、硫黄のように約20個の不安定同位体と４つの安定同位体を持つような元素もありますし、スズは陽子数が魔法数の50であるので10種類もの安定な同位体を持っています。元素比という時には、これら同位体効果が縮退していることも知っておくとよいです。別の言い方をすると、 原子核が安定かどうかは原子核物理学に直結し、元素の存在度は何10億年もかけた自然現象のスナップショットであり、両者を直接結びつけるのは少しギャップがあります。安定同位体や不安定同位体の動きも含めて捉えるのも大切ということです。同位体分析は重要で、隕石は質量分析などで高精度で研究できますが、宇宙観測で同位体を決めるのはかなり難しいです。
    • 鉛よりも重たい元素は、ウラン系列、トリウム系列、ネプツニウム系列、アクチニウム系列などの壊変系列(一回の崩壊で基底状態になるのではなく、何回も崩壊を繰り返して安定核にたどり着く)を形成します。カリウム40のように、系列を構成しないものもあります。例えば、カリウム40が45年前に一気に生成し、地球の残っているとすると、半減期が12.5億年なので、45億年前は一桁以上(~=2^4)もあることになります。このように、同位体まで含めると、元素の量は時間変化するもので、逆にこれを活用して、過去を知ることもできます。地球には何故放射能があるのか?自然界における放射線 飯塚毅氏 をぜひ一読ください。

  • 細かい話

    • 隕石の人は、Si=10^6個で規格化、天文の人は、水素=10^12個で規格化するので、換算を間違えると大きく異なる。。単に、宇宙観測では水素はどこにでもあるが、Siが検出できるとは限らないのに対して、地球上の表層に存在する元素で一番多いのが酸素で約50%で次がケイ素の約25%だからであろう。

雑多な情報

周期表の元素ごとの雑多な情報は、

にまとまってたりしますが、やや広告が多い。

2
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?