AIとか機械学習とかが社会全体に浸透し始めてる昨今、必要な知識を、Pythonで基礎から学習してみる。
線形代数とは
線形空間(ベクトル空間)や線形変換(ベクトル変換)といった概念を扱う。
直線や平面、空間といった図形的な性質と、それらの上での変換(回転、拡大縮小、せん断など)を数式を使って表現し、分析するもの。
活用例:
画像処理、コンピュータグラフィックス、機械学習、データ分析、物理シミュレーションなど
ベクトルとは
ベクトルは、大きさと向きを持つ量。
矢印で表現されることが多く、矢印の長さがベクトルの大きさを、矢印の向きがベクトルの向きを表す。
ベクトルは、複数の数値を並べたものとして表現できる。
例えば、
2次元ベクトル:(x, y)のように、x 成分とy 成分の2つの数値で表現される
3次元ベクトル:(x, y, z)のように3つの数値で表現される
これらの数値は、ベクトルの成分と呼ばれる。
ベクトルの和
2つのベクトルを足し合わせる操作。
一方のベクトルの終点に、もう一方のベクトルの始点をくっつけることで、新たなベクトルが得られる。
この新たなベクトルが、2つのベクトルの和となる。
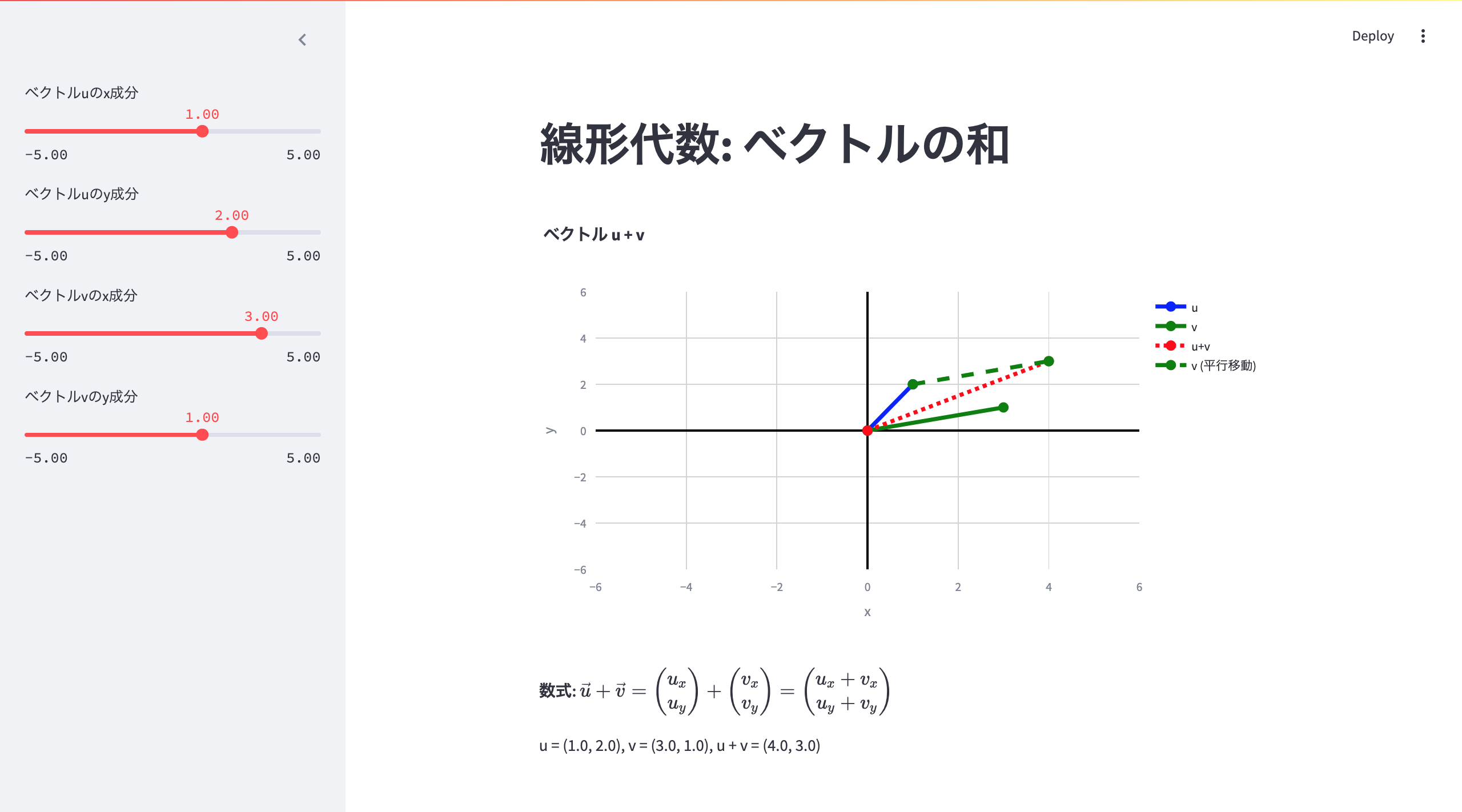
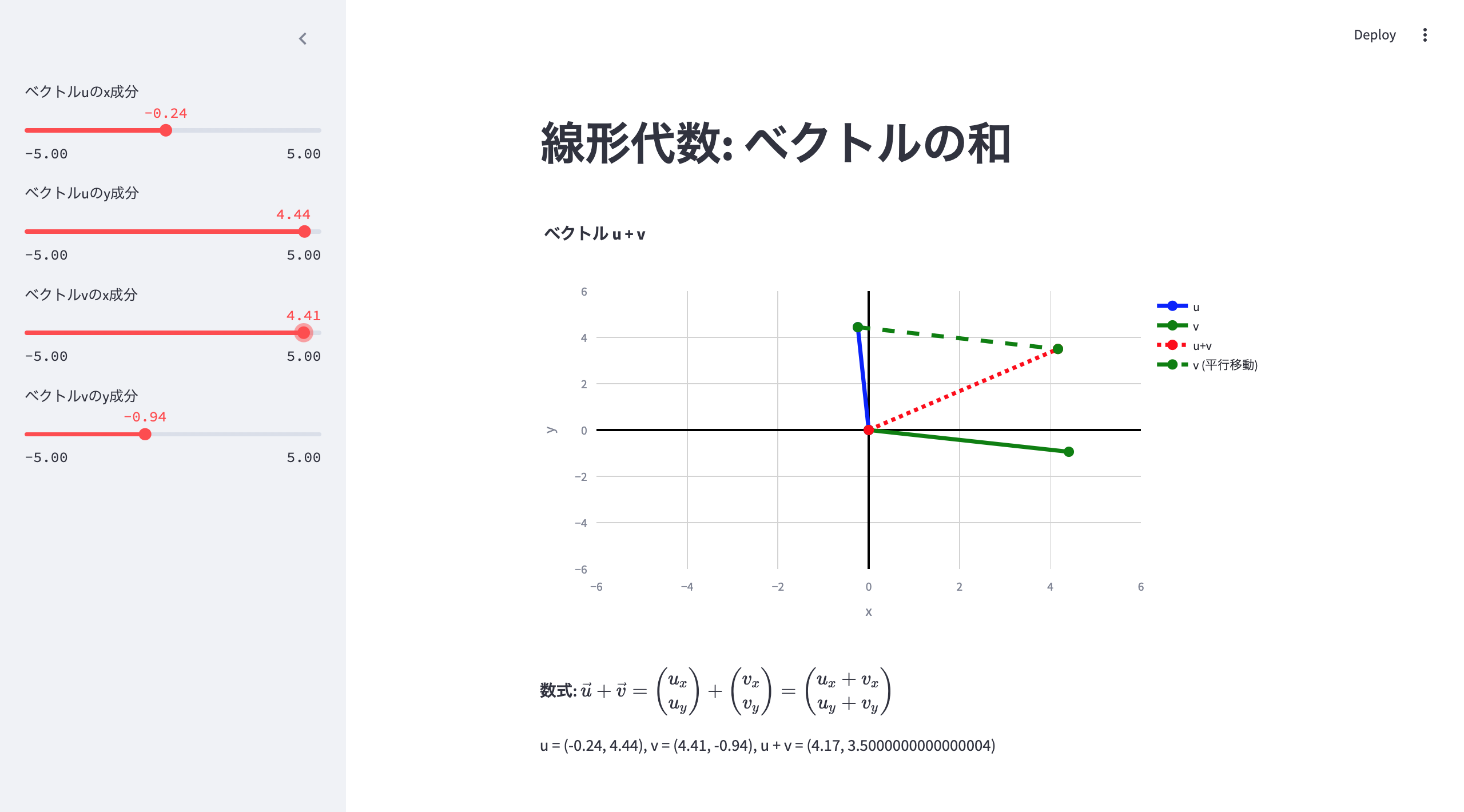
・ベクトル u = (u_x, u_y)
・ベクトル v = (v_x, v_y)
の和を w とすると
w = (u_x + v_x, u_y + v_y) となる。
つまり、対応する成分同士を足し合わせることで、ベクトルの加算が行われます。
コード
視覚的に操作したいので、streamlitを使う。
import streamlit as st # Webアプリ作成用
import plotly.graph_objects as go # グラフ作成用
import numpy as np # 数値計算用
# タイトル
st.title("線形代数: ベクトルの加算")
# サイドバーにスライダーを設置
u_x = st.sidebar.slider("ベクトルuのx成分", -5.0, 5.0, 1.0)
u_y = st.sidebar.slider("ベクトルuのy成分", -5.0, 5.0, 2.0)
v_x = st.sidebar.slider("ベクトルvのx成分", -5.0, 5.0, 3.0)
v_y = st.sidebar.slider("ベクトルvのy成分", -5.0, 5.0, 1.0)
# ベクトルu, v, u+vを定義
u = np.array([u_x, u_y])
v = np.array([v_x, v_y])
w = u + v # ベクトルuとvの加算
# Plotlyでグラフを作成
fig = go.Figure()
# ベクトルuを描画 (原点から(u_x, u_y)まで)
fig.add_trace(go.Scatter(x=[0, u[0]], y=[0, u[1]], mode="lines+markers", name="u", marker=dict(size=10), line=dict(width=4, color="blue")))
# ベクトルvを描画 (原点から(v_x, v_y)まで)
fig.add_trace(go.Scatter(x=[0, v[0]], y=[0, v[1]], mode="lines+markers", name="v", marker=dict(size=10), line=dict(width=4, color="green")))
# ベクトルu+vを描画 (原点から(w_x, w_y)まで)
fig.add_trace(go.Scatter(x=[0, w[0]], y=[0, w[1]], mode="lines+markers", name="u+v", marker=dict(size=10), line=dict(width=4, dash="dot", color="red")))
# 平行移動したベクトルvを描画 (ベクトルuの先端からu+vの先端まで)
fig.add_trace(go.Scatter(x=[u[0], w[0]], y=[u[1], w[1]], mode="lines+markers", name="v (平行移動)", marker=dict(size=10), line=dict(width=4, dash="dash", color="green")))
# グラフのレイアウトを設定
fig.update_layout(
xaxis_title="x", # x軸のラベル
yaxis_title="y", # y軸のラベル
xaxis=dict(range=[-6, 6], zeroline=True, zerolinewidth=2, zerolinecolor='black', showgrid=True, gridwidth=1, gridcolor='lightgray'), # x軸の範囲、ゼロ線、グリッド線など
yaxis=dict(range=[-6, 6], zeroline=True, zerolinewidth=2, zerolinecolor='black', showgrid=True, gridwidth=1, gridcolor='lightgray'), # y軸の範囲、ゼロ線、グリッド線など
title="ベクトル u + v" # グラフのタイトル
)
# Streamlitでグラフ表示
st.plotly_chart(fig)
# 数式とベクトルの成分を表示
st.markdown(r"**数式:** $\vec{u} + \vec{v} = \begin{pmatrix} u_x \\ u_y \end{pmatrix} + \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} u_x + v_x \\ u_y + v_y \end{pmatrix}$")
st.write(f"u = ({u_x}, {u_y}), v = ({v_x}, {v_y}), u + v = ({w[0]}, {w[1]})")
実行結果
streamlit run main.py
実行するとメールアドレスの入力を促されます。
👋 Welcome to Streamlit!
If you’d like to receive helpful onboarding emails, news, offers, promotions,
and the occasional swag, please enter your email address below. Otherwise,
leave this field blank.
Email: xxxxx@xxx.xx
入力して Enter でブラウザが起動。
You can find our privacy policy at https://streamlit.io/privacy-policy
Summary:
- This open source library collects usage statistics.
- We cannot see and do not store information contained inside Streamlit apps,
such as text, charts, images, etc.
- Telemetry data is stored in servers in the United States.
- If you'd like to opt out, add the following to ~/.streamlit/config.toml,
creating that file if necessary:
[browser]
gatherUsageStats = false
You can now view your Streamlit app in your browser.
Local URL: http://localhost:8501
Network URL: http://192.168.1.100:8501
For better performance, install the Watchdog module:
$ xcode-select --install
$ pip install watchdog
起動すると、グラフと数式が表示されます。
サイドバーで値を変更できます。
まとめ
今回は、線形代数からベクトルの和について、Pythonで学習してみました。
視覚的に操作できると、分かりやすいですね。
プログラミングもできて一石二鳥なので、継続してみようと思います。