学習メモ ゼロから作るDeep Learning
使いそうな関数メモ
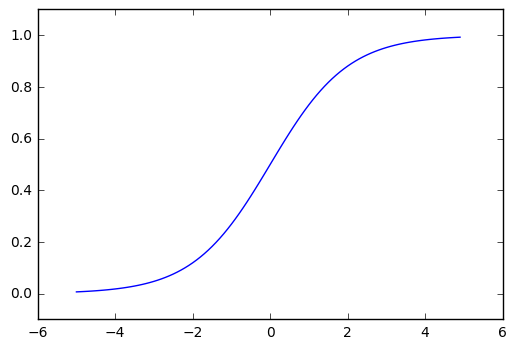
シグモイド関数:sigmoid
重要な性質:0から1の間を返す、滑らか、(書籍には記述がないが)単調増加
h(x) = \frac{1}{1+\exp(-x)}
def sigmoid(x):
return 1/(1+np.exp(-x))
ソフトマックス関数
結局適応してもしなくても最大値を探すので出力層のソフトマックス関数は省略するのが一般的とのこと
y_k = \frac{\exp(a_k)}{\sum_{i=1}^{n}\exp(a_i)} = \frac{\exp(a_k + C')}{\sum_{i=1}^{n}\exp(a_i + C')}
def softmax(a) :
c = np.max(a)
exp_a = np.exp(a - c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
損失関数
損失関数を設定する理由
認識精度を指標するするとパラメータの微分がほとんどの場所で0(動かなくなる)になるから
2乗和誤差:mean squared error
E = \frac{1}{2}\sum_{k=1} (y_k - t_k)^2
def mean_squared_error(y,t):
return 0.5 * np.sum((y-t)**2)
交差エントロピー誤差:cross entropy error
ポイント:one-hot表現 正解ラベルだけ1、他は0(ラベルはt)
E=\sum_{k=1} - t_k \log y_k
def cross_entropy_error(y, t) :
delta = le-7
return -np.sum(t*np.log(y+delta))
ミニバッチ対応版 交差エントロピー誤差:cross entropy error
ミニバッチ(小さな塊):データの中から一部を選び出し、その一部のデータを全体の「近似」として利用
ポイント:one-hotでは不正解のラベルは0になる(=誤差は0)のため無視して良い
訓練データの数に関係なく統一した指標が得られるようにNで割る
E=-\frac{1}{N}\sum_{n}\sum_{k=1} t_{nk} \log y_{nk}
def cross_entropy_error(y, t) :
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t*np.log(y[np.arange(bathch_size), t])) / bathc_size
微分
数値微分
ポイント:丸め誤差を生じさせないように1e-4程度にする
def numerical_diff(f, x) :
h = 1e-4
return (f(x+h)-f(x-h))/(2*h)
偏微分
# x1=4の時
def function_tmp1(x0):
return x0*x0 + 4.0*2.0
numerical_diff(function_tmp1, 3.0)
勾配
勾配:すべての変数の偏微分をベクトルとしてまとめたもの
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x) #xと同じ形状の配列を生成、ここに値を詰めていく
# 要は変数を一つずつ順番に微分しているだけ
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
return grad
勾配法:gradient method
勾配法:勾配方向に移動を繰り返し行い、関数の値を徐々に減らしていく
ポイント:勾配法で達するのは極小値で最小値ではない
イメージはCoursera のAndrew Ng先生 Machine Learning Week5 Lecture9 p.31が分かり易い
x_0=x_0-\eta\frac{\partial f}{\partial x_0} \\
x_1=x_1-\eta\frac{\partial f}{\partial x_1} \\
\\
\eta : 学習率(一回の学習でどれだけ学習するか、大きすぎても小さすぎてもいけない)
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x
def function_2(x):
return x[0]**2 + x[1]**2
init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100)
上記のような学習率のような人の手によって設定されるパラメータをハイパーパラメータと言う
ニューラルネットワークに対する勾配
W = \biggl(\begin{matrix}
w_{11} & w_{21} & w_{31} \\
w_{12} & w_{22} & w_{32}
\end{matrix}\biggr)\\
\frac{\partial L}{\partial W} = \Biggl(\begin{matrix}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{31}}\\
\frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{32}}
\end{matrix}\Biggr)\\
\frac{\partial L}{\partial w_{11}} : w_{11}を少し変化させると損失関数Lがどれだけ変化するかを表す
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common.functions import softmax, cross_entropy_error
from common.gradient import numerical_gradient
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self, x):
return np.dot(x, self.W)
def loss(self, x, t):
z = self.predict(x)
y = softmax(z)
loss = cross_entropy_error(y, t)
return loss
# 使ってみる
# パラメータ
x = np.array([0.6, 0.9])
# ラベル
t = np.array([0, 0, 1])
net = simpleNet()
f = lambda w: net.loss(x, t)
# 要は損失関数が極小値となるものを探す勾配法を動かしている
dW = numerical_gradient(f, net.W)
print(dW)
[[ 0.10181684 0.35488728 -0.45670412]
[ 0.15272526 0.53233092 -0.68505618]]
上記結果はw_11をhだけ増やすと0.10181684だけ増加するということ
貢献度合ではw_23が最も大きい
# ラムダ式
myfunc = lambda x: x ** 2
myfunc(5) # 25
myfunc(6) # 36
# これは、下記と同じ
def myfunc(x):
return x ** 2
学習アルゴリズムの実装
学習の概要
ニューラルネットワークの学習:重みとバイアスを訓練データに適応するように調整すること
手順
ステップ1:ミニバッチ
訓練データの中からランダムに一部のデータを選び出す。(ミニバッチ)
このミニバッチの損失関数の値を減らすことを目的とする
ステップ2:勾配の算出
ミニバッチの損失関数を減らすために、各重みパラメータの勾配を求める。
勾配は、損失関数の値を最も減らす方向を示す
ステップ3:パラメータの更新
重みパラメータを勾配方向に微少量だけ更新する。
ステップ4:繰り返し
ステップ1〜3を繰り返す
用語
確率的勾配降下法(SGD Stochastic gradient descent):
確率的:「確率的に無作為に選び出した」
勾配降下法※:「最小値を探す」
※勾配上昇法もあり、本質的に符合を反転させれば同じ問題なので本質的には需要ではない
エポック:epoch
1エポックとは学習において訓練データを全て使い切った回数に対応
例:データ数10,000の訓練データ、100個のミニバッチの際には確率的勾配降下法を100回繰り返すこと
実装と解説
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
# 初期化
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 認識(推論)を行う。引数のxは画像データ
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# 損失関数を求める
# x:入力データ, t:教師データ
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
# 認識精度を求める
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
#重みパラメータに対する勾配を求める
# x:入力データ, t:教師データ
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
わかりづらいの図示
この絵のような計算を行列計算で一気に行っているだけ
絵はCoursera のAndrew Ng先生 Machine Learning Week5 Lecture9 p.13の方が分かり易い

ミニバッチ学習、テストデータで評価
勾配法を繰り返して精度をあげるだけなので省略
テストデータでの評価も過学習かどうかを判定しようとテストデータの精度を図示しているだけなので省略