ゼロから作るDeep Learning 6章
Deep Learningと言わず
Machine Learningでかなり大切な事を扱っているのがこの6章になります。
パラメータの更新
ニューラルネットワークの目的=損失関数の値をできるだけ小さくするパラメータを見つけること
そのような問題を解くことを「最適化」と言う
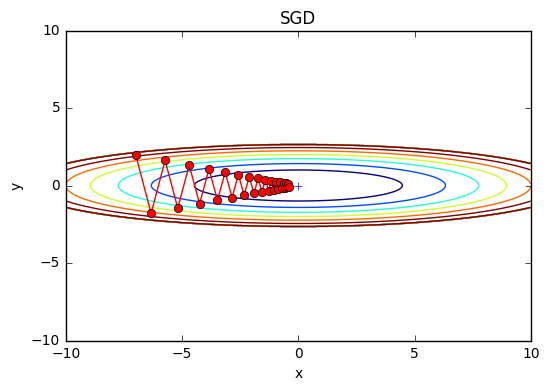
SGD:確率的勾配降下法
W \leftarrow W - \eta\frac{\partial L}{\partial W}
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
network = TwoLayerNet(...)
# optimizer:最適化を行う者
optimizer = SGD()
for i in range(10000) :
...
x_bath, t_bath = get_mini_batch(...)
grads = network.gradient(x_batch, t_batch)
params = network.params
optimizer.update(params, grads)
...
パラメータの更新はopetimizerが行う
実施するのはoptimizerにパラメータと勾配の情報を渡すだけ
上記のように最適化を行うクラスを分離して実装することで、機能のモジュール化が容易になる
例えば次に出てくるMomentumという別の最適化手法を実装する際にも、同じくupdate(params, grads)という共通メソッドを持つように実装する
するとoptimizer = SGD()をoptimizer = Momentum()に変更するだけで、SGDをMomentumに切り替えることが可能になる
SGDの欠点
SGDの欠点は、関数の形状が等方的出ないと出ないと(伸びた形の関数だと)非効率的な経路で検索することになる
なお、上記の欠点の根本的な原因は、勾配の方向が本来の最小値ではない方向を指していることに起因します
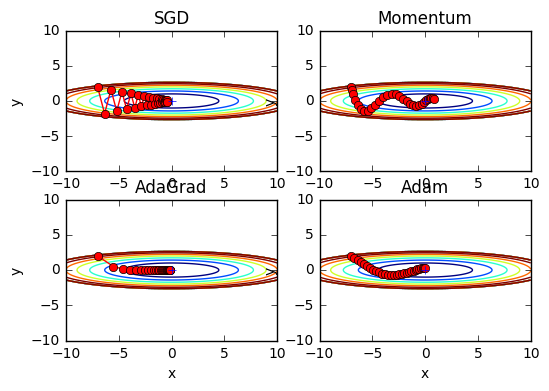
このSGDの欠点を改善するために、SGDに代わる手法として3つの手法が紹介
・Momentum
・AdaGrad
・Adam
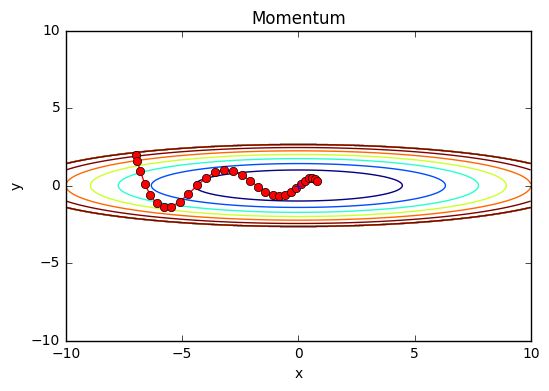
Momentum
モーメンタン(Momentum)とは「運動量」のこと
地面を転がるボールが、何も力を受けない時に徐々に摩擦や空気抵抗で減速するようなイメージ
v \leftarrow \alpha v - \eta\frac{\partial L}{\partial W}\\
W \leftarrow W + v
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr * grads[key]
param[key] += self.v[key]
x軸方向:受ける力は小さいが、常に同じ方向の力を向けるため、同じ方向へ一定して加速することになる
y軸方向:受ける力は大きいが、正と負の方向の力を交互に受け歌め、互いに打ち消し合い、y軸への速度は安定しない
→SGDよりx軸方向へ早く近づけ、ジグザグの動きを軽減できる
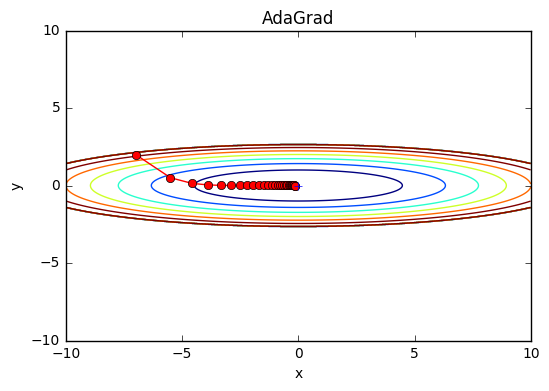
AdaGrad
この手法は学習係数の低減(learning rate decay)行う
これは学習が進むにつれて学習係数を小さくするという手法です
Ada:適応的のAdaptiveに由来
h \leftarrow h + \frac{\partial L}{\partial W}\odot\frac{\partial L}{\partial W}\\
W \leftarrow W - \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W}
1/√hを乗算することは、パラメータの更新の中でよく動いた(大きく更新された)要素は、学習係数が小さくなることを意味する
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
param[key] += self.lr * grads[key] / (np.sqrt(self.h[key] + le-7)
le-7という小さい値を加算しているのはself.h[key]の中に0があった場合、0で除算されてしまうからです
RMSProp
AdaGradは過去の勾配を2乗和として全て記録します
そのため学習を無限に進めれば更新料は0になり、全く更新されなくなリます
この問題がを解決したRMSPropと違う手法もあります
RMSPropはかこ全ての勾配を均一に加算するのではなく、過去の勾配を徐々に忘れて、新しい勾配情報が大きく反映させるように計算される手法です
これを「指数移動平均」と言います
本には式は載っていないがプログラムから逆算するにこんな計算式に見える
\begin{align}
初期値d&=0.99\\
h &\leftarrow h * d + (1 - d)\frac{\partial L}{\partial W}\odot\frac{\partial L}{\partial W}\\
W &\leftarrow W - \eta \frac{1}{\sqrt{h}} \frac{\partial L}{\partial W}
\end{align}
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
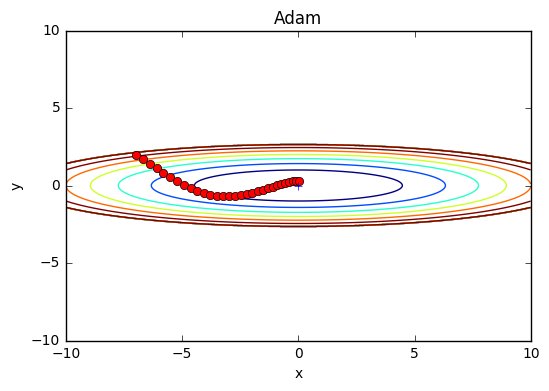
Adam
Momentum:物理法則に準じる動き
AdaGrad:パラメータの要素ごとに、適応的に更新ステップを調整
Adam = Momentum + AdaGrad + ハイパーパラメータの「バイアス補正(偏りの補正)」
同じく本には数式は載っておらず
ググったら数式は出てきたのでそちらを確認
引用:http://postd.cc/optimizing-gradient-descent/#adam
Adam(Adaptive Moment Estimation)14はまた別の方式で、それぞれのパラメータに対し学習率を計算し適応させていきます。
AdadeltaやRMSpropでは、過去の勾配の二乗v_tの指数関数的減衰平均を蓄積していました。Adamではこれに加え、同じように過去の勾配m_tの指数関数的減数平均を保持します。Momentumと似た方法です。
\begin{align}
初期値\beta_1 &= 0.9,\beta_2=0.999,\epsilon=10^{-8}\\
\\
m_t &= \beta_1 m_{t-1} + (1 – \beta_1) g_t\\
v_t &= \beta_2 v_{t-1} + (1 – \beta_2) g_t^2\\
\\
\hat{m}_t &= \dfrac{m_t}{1 – \beta^t_1}\\
\hat{v}_t &= \dfrac{v_t}{1 – \beta^t_2}\\
\\
\theta_{t+1} &= \theta_{t} – \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t\\
\end{align}
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
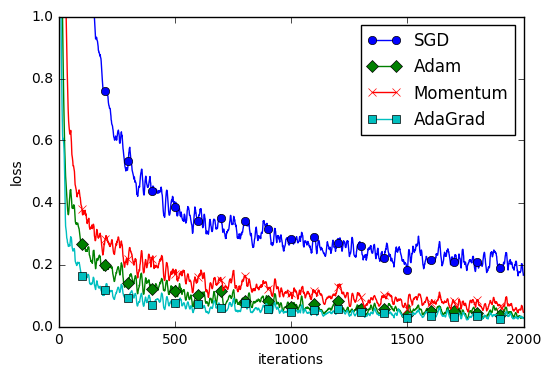
比較
下記画像ではAdaGradが良さそうです
しかし残念ながらどの手法が優れているということは(今の所)ありません
それぞれに特徴があり、得意な問題、不得意な問題があるそうです
重みの初期値
重みの初期値を0とした時の問題点
過学習を抑え、汎化性能を高めるテクニック、Weight decay(荷重減衰)
Weight decay:重みパラメータの値を小さくするように学習を行うことを目的とした手法
重みの値を小さくすることで、過学習が起きにくくなリマす。
重みを小さくしたいのであれば、初期値もできるだけ小さい値でスタートしたいと思うのが当然です
これまでの重みの初期値、0.01 * np.random.randn(10, 100)でした。
(標準偏差が0.01のガウス分布)
しかし重みが0の際には悪いアイディアだそうです。
(正確には重みの値を均一な値に設定してはいけない)
理由は、誤差伝播法において、全ての重みの値が均一の更新されてしまうからです。
そのためランダムな初期値が必要になります。
重みの初期値のベストプラクティス
結論を先に述べると以下になります。
- 活性化関数にReLUを使う場合は「Heの初期値」
- sigmoidやtanhなどのS字カーブの時は「Xavierの初期値」
前層のノードの個数がnの際に
Xavierの初期値:標準偏差が\frac{1}{\sqrt{n}}の標準偏差を持つガウス分布\\
Heの初期値:標準偏差が\sqrt\frac{2}{n}の標準偏差を持つガウス分布\\
隠れ層のアクティベーション分布(活性化関数の後の出力データ)
0と1に偏ったデータ
→逆伝播の勾配の値がどんどん小さくなって消えていく
この問題を「勾配消失」と言います
各ニューロンがほぼ同じ値を出力する
→アクティベーションの偏り
「表現力の制限」という問題になる
そのため程よくばらけている結果が望ましい
- 活性化関数にsigmoidを使用した際のアクティベーション分布の変化
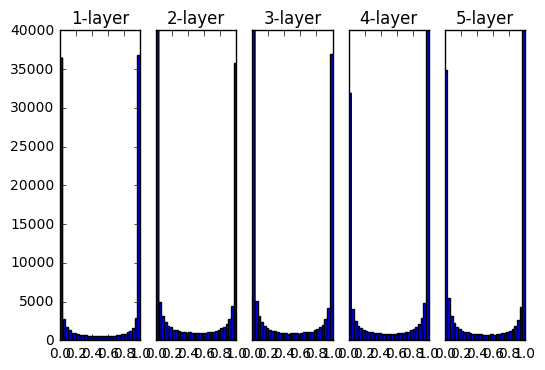
重みの初期値として標準偏差1のガウス分布を用いた時の各層のアクティベーションの分布
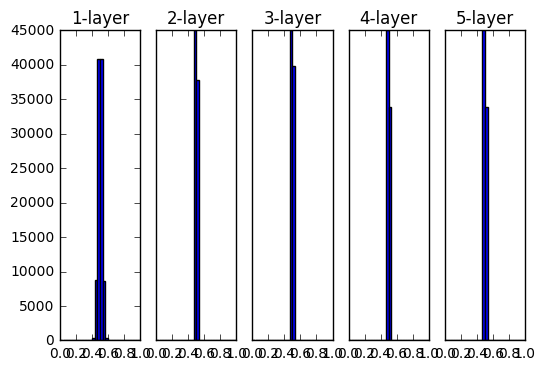
重みの初期値として標準偏差0.01のガウス分布を用いた時の各層のアクティベーションの分布
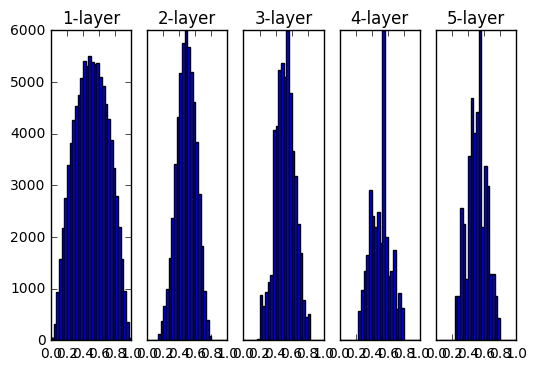
重みの初期値としてXavierの初期値を用いた時の各層のアクティベーションの分布
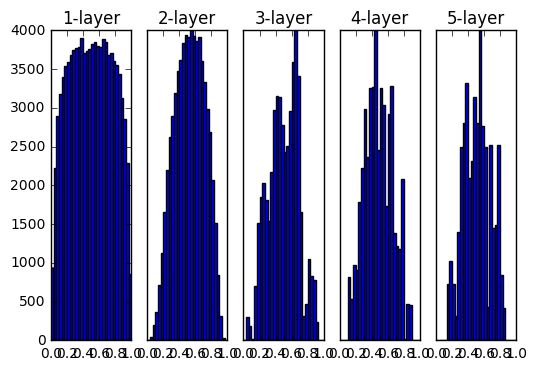
重みの初期値としてHeの初期値を用いた時の各層のアクティベーションの分布
- 活性化関数にReLUを使用した際のアクティベーション分布の変化
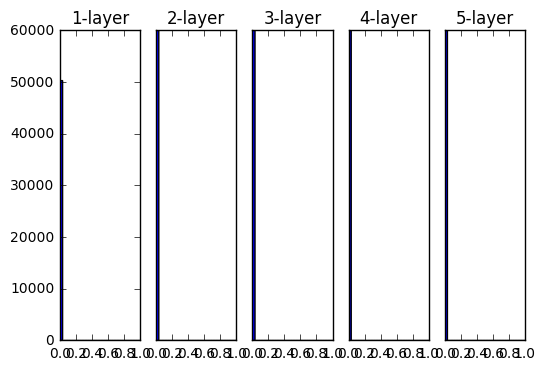
重みの初期値として標準偏差1のガウス分布を用いた時の各層のアクティベーションの分布
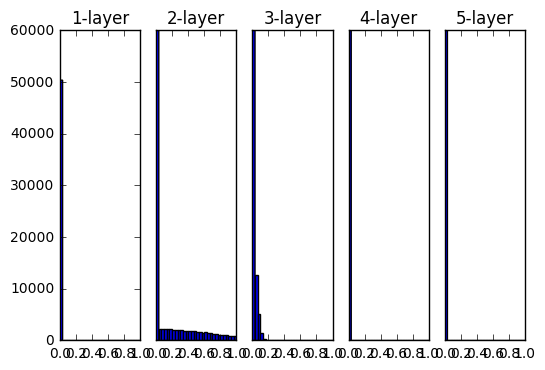
重みの初期値として標準偏差0.01のガウス分布を用いた時の各層のアクティベーションの分布
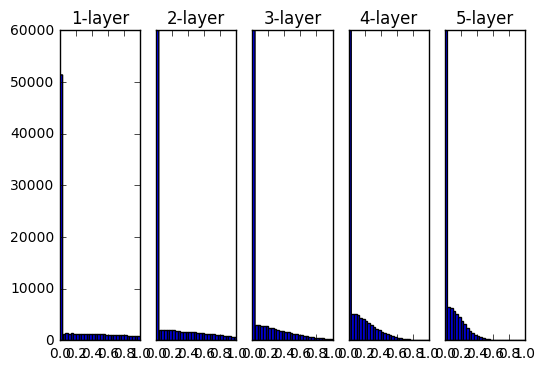
重みの初期値としてXavierの初期値を用いた時の各層のアクティベーションの分布
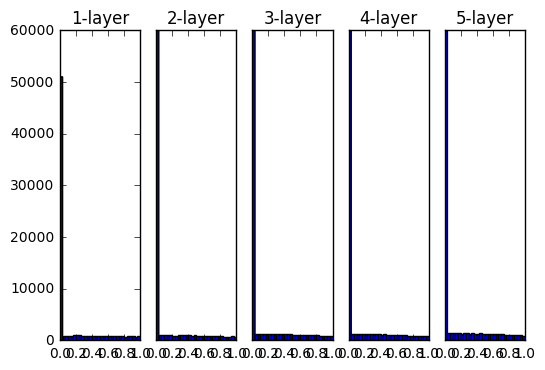
重みの初期値としてHeの初期値を用いた時の各層のアクティベーションの分布
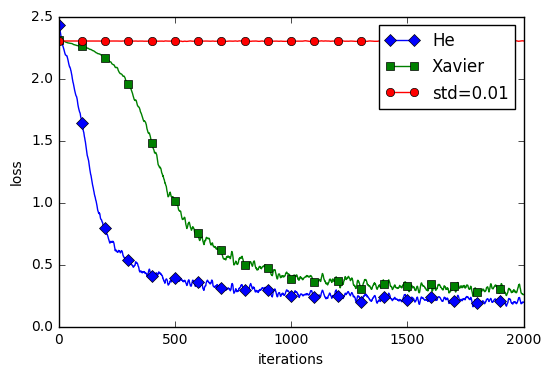
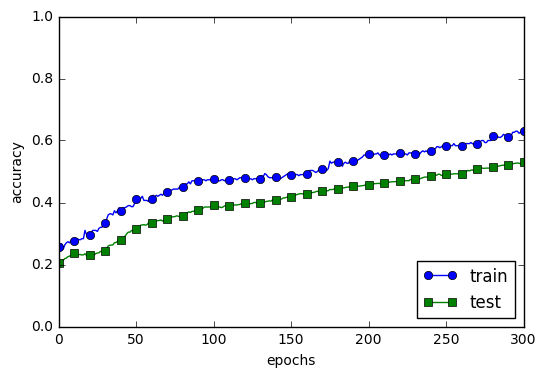
MNISTデータセットによる重みの比較
std=0.01の場合はほとんど学習が進んでいおらず
He、Xavierの際にはサクサク学習が進んでいる
→初期値の問題はとても重要ということがわかります
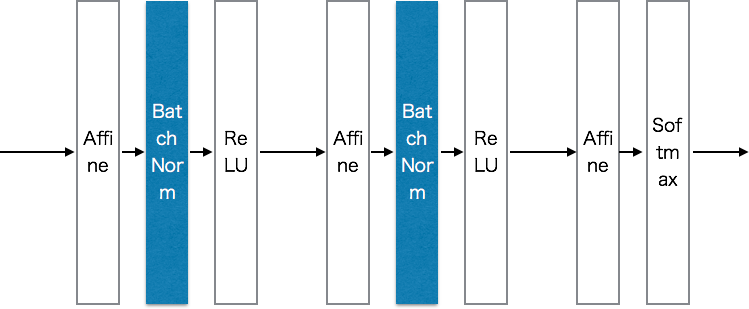
Batch Normalization
各層のアクティベーションの分布が適度な広がりを持つように”強制的”にアクティベーションの調整を行う
Batch Normalizationの利点
- 学習を早く進行させることができる(学習係数を大きくすることができる)
- 初期値にそれほど依存しない(初期値に対してそこまで神経質にならなくて良い)
- 過学習を抑制する(Dropoutなどの必要性を減らす)
なんだか私見ですが料理の味の素みたいですね
Batch Normalizationアルゴリズム
各層のアクティベーションの分布が適度な広がりを持つように調整する
→つまりデータ分布の正規化(平均が0、分散が1の分布)を行うレイヤをニューラルネットワークに挿入する
\begin{align}
&ミニバッチとしてB=\{x_1, x_2, \cdots, x_m\}というm個の入力データの集合に対して、\\
&平均\mu_B、 分散\sigma_B^2を求める \\
&また\epsilonは10^{-7}などのとても小さな値
\end{align}
\begin{align}
\mu_B &\leftarrow \frac{1}{m} \sum_{i-1}^{m} x_i\\
\sigma_B^2 &\leftarrow \frac{1}{m} \sum_{i-1}^{m} (x_i - \mu_B)^2\\
\hat{x_i} &\leftarrow \frac{x_i-\mu_B}{\sqrt{\sigma_B^2 + \epsilon}}
\end{align}
さらにBath Normレイヤは、この正規化されたデータに対して、固有のスケールとシフトで変換を行います。
γ、βはパラメータで、最初はγ=1、β=0からスタートして、学習によって適した値に調整されていきます
y_i \leftarrow \gamma \hat{x_i} + \beta
逆伝播などは
Frederik Kratzertのブログを読めとのことでした。
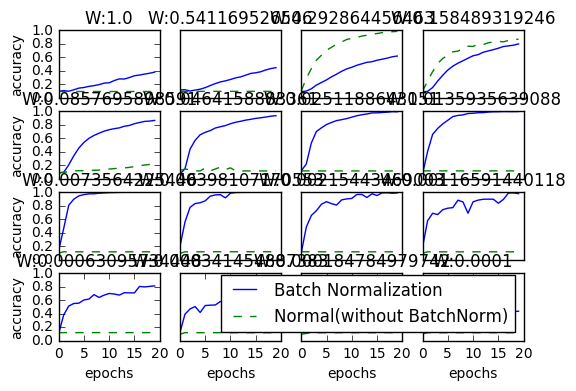
Batch Normalizationの評価
正則化
過学習
過学習が起きる原因
・パラメータを大量に持ち、表現力の高いモデルである事
・訓練データが少ない事
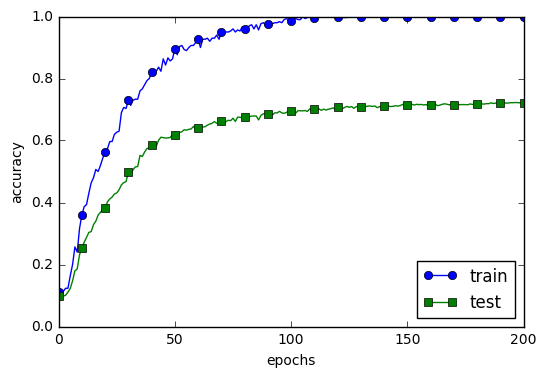
過学習をわざと発生させた
Weight decay
Weight decay:荷重減衰
ニューラルネットの学習目的は損失関数の値を小さくする事
この際に重みの2重ノルム(L2ノルム)を加算してあげれば、重みが大きくなる事を抑えられる
重みWとすれば、L2ノルムのWeight decayは
\frac{1}{2}\lambda W^2
λは正則化の強さをコントロールするハイパーパラメータ
1/2はW^2を微分した結果をλWにするための調整用の定数
L2ノルム
\sqrt{w_1^2+w_2^2+\cdots+w_n^2}
L1ノルム
|w_1^2|+|w_2^2|+\cdots+|w_n^2|
正直本の説明よりも他を参照した方がわかりやすかった
引用:http://qiita.com/supersaiakujin/items/97f4c0017ef76e547976
deep neural networkではlayerが多層になるほど、そのモデルの表現能力が増します。
しかし、多層になるほどoverfittingのリスクも高くなります。
Modelの表現能力を維持したまま、parameterの自由度に制限を与えることでoverfittingのリスクを減らすことが行われます。
その手法の一つがweight decay(重み減衰)です。
weightの更新式は下記のように書かれます。
{w \leftarrow w -\eta \frac{\partial C(w)}{\partial w} - \eta \lambda w\\
}
上記式は何がしたいのか少しわかりづらいですが、実際はcost functionを下記のようにしたものから来ています。
{\tilde C(w) = C(w) + \frac{\lambda}{2}||w||^2
}
これはつまり、cost functionにL2 regularization項をつけたものです。
この項によりweightの値は小さくなります。
なので、実際に実装するときはL2 regularizationの項をcostに加えることになります。
テキストではスルーされているが使っている部分のソースだけ抜粋:weight_decay_lambdaで検索すればわかりやすい
初期化、損失関数の計算、重みの設定の際に使用している
def __init__(self, input_size, hidden_size_list, output_size,
activation='relu', weight_init_std='relu', weight_decay_lambda=0):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.weight_decay_lambda = weight_decay_lambda
self.params = {}
# 重みの初期化
self.__init_weight(weight_init_std)
# レイヤの生成
activation_layer = {'sigmoid': Sigmoid, 'relu': Relu}
self.layers = OrderedDict()
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)],
self.params['b' + str(idx)])
self.last_layer = SoftmaxWithLoss()
def loss(self, x, t):
"""損失関数を求める
Parameters
----------
x : 入力データ
t : 教師ラベル
Returns
-------
損失関数の値
"""
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2)
return self.last_layer.forward(y, t) + weight_decay
def gradient(self, x, t):
"""勾配を求める(誤差逆伝搬法)
Parameters
----------
x : 入力データ
t : 教師ラベル
Returns
-------
各層の勾配を持ったディクショナリ変数
grads['W1']、grads['W2']、...は各層の重み
grads['b1']、grads['b2']、...は各層のバイアス
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grads = {}
for idx in range(1, self.hidden_layer_num+2):
grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W
grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grads
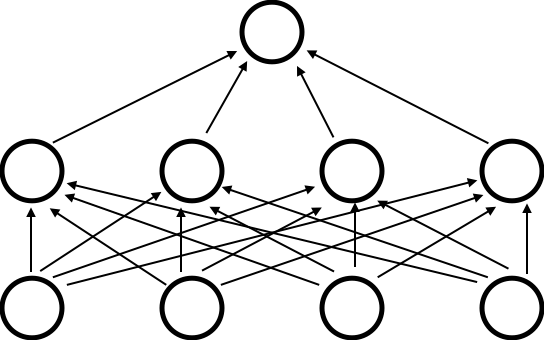
Dropout
Dropout:ニューロンをランダムに消去しながら学習する手法
Chainerで実装されるDropout
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
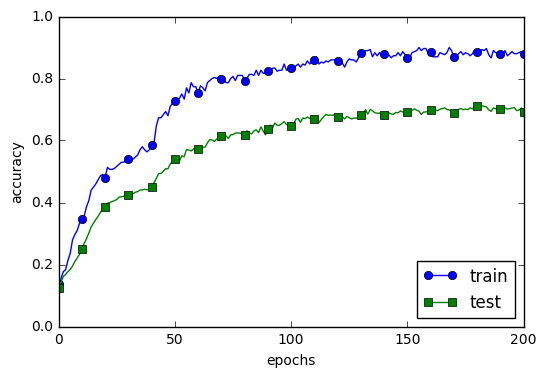
Dropoutを使用した際の結果
ハイパーパラメータの検証
これまでのハイパーパラメータ例
・各層のニューロンの数
・バッチサイズ
・学習係数
・Weight decay
検証データ
ハイパーパラメータはテストデータで性能を評価してはいけない
→過学習を起こす起こす事になるから
そのため、ハイパーパラメータ専用の確認データ、*検証データ(validation data)*を使用する
データの内容によってはユーザの手で作る必要がある
訓練データから20%程度検証データとして先に分離するコード
(x_train, t_train), (x_test, t_test) = load_mnist()
# 訓練データをシャッフル
x_train, t_train = shuffle_dataset(x_train, t_train)
# 検証データの分割
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_val - x_train[:validation_num]
t_val - t_train[:validation_num]
x_train - x_train[validation_num:]
t_train - t_train[validation_num:]
ハイパーパラメータの最適化
ハイパーパラメータの最適化には次のステップを繰り返す
-
STEP0
ハイパーパラメータの範囲を指定する:最初はざっくりと指定でOK -
STEP1
設定されたハイパーパラメータの範囲からランダムにサンプリングする -
STEP2
STEP1でサンプリングされたハイパーパラメータの値を使用して学習を行い、
喧騒データの認識精度を評価する
(ただし、エポックは小さく設定) -
STEP3
STEP21とSTEP2wpある回数(100回など)繰り返し、それらの認識精度の結果から
ハイパーパラメータの範囲を狭める
ランダムサンプリングの実装
wight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
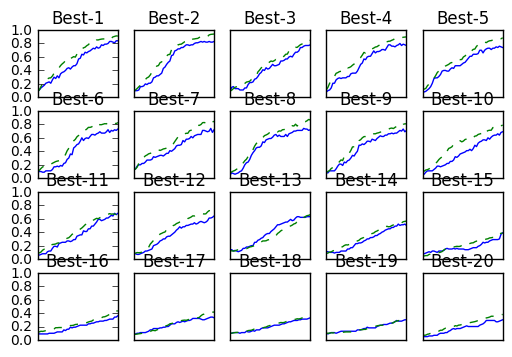
Best-1(val acc:0.84) | lr:0.008596628403945712, weight decay:3.075068633526172e-06
Best-2(val acc:0.83) | lr:0.009688160706596694, weight decay:5.876005684736357e-08
Best-3(val acc:0.78) | lr:0.007897858091143213, weight decay:3.792675246120474e-08
Best-4(val acc:0.77) | lr:0.008962267845301249, weight decay:4.0961888275354916e-07
Best-5(val acc:0.74) | lr:0.009453193380059509, weight decay:1.5625175027026464e-08
Best-6(val acc:0.73) | lr:0.0066257479672272536, weight decay:4.6591905625864734e-05
Best-7(val acc:0.72) | lr:0.007814005955583136, weight decay:4.9330072714643424e-06
Best-8(val acc:0.72) | lr:0.008895526423573389, weight decay:4.297901358238285e-06
Best-9(val acc:0.71) | lr:0.006419577071135049, weight decay:1.0848308972057103e-08
Best-10(val acc:0.69) | lr:0.006304961469167366, weight decay:1.6652787617252613e-07
上記の結果をみると次ぐらいか?
wight_decay:10^-5-10^-8
lr:0.01-0,0001
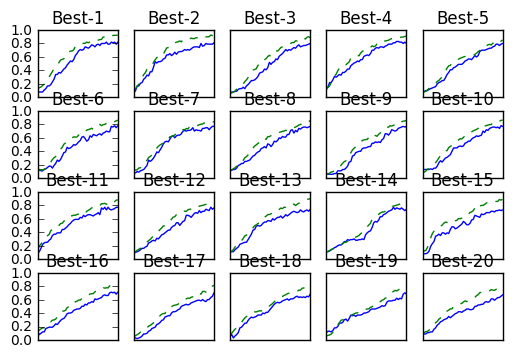
絞ってからもう一度実行
Best-1(val acc:0.82) | lr:0.009567378324697062, weight decay:8.329914422037397e-07
Best-2(val acc:0.81) | lr:0.009548817455702163, weight decay:1.9982550859731867e-08
Best-3(val acc:0.8) | lr:0.009291306660458992, weight decay:2.2402127139457002e-07
Best-4(val acc:0.8) | lr:0.008381207344259718, weight decay:8.66434339086022e-08
Best-5(val acc:0.8) | lr:0.009034895918329205, weight decay:1.2694550788849033e-08
Best-6(val acc:0.78) | lr:0.0057717685490679006, weight decay:5.933415739833589e-08
Best-7(val acc:0.77) | lr:0.005287013083466725, weight decay:5.585759633899539e-06
Best-8(val acc:0.77) | lr:0.006997138970399023, weight decay:3.1968420191793365e-06
Best-9(val acc:0.77) | lr:0.007756581950864435, weight decay:1.0281187459919625e-08
Best-10(val acc:0.77) | lr:0.008298200180190944, weight decay:7.389218444784364e-06
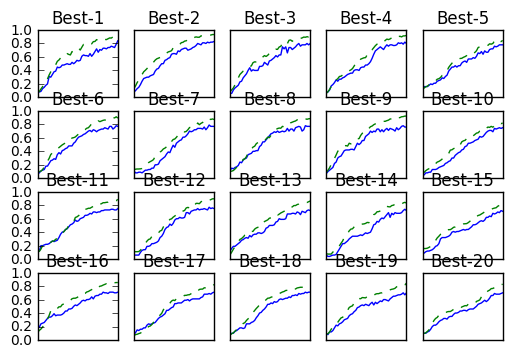
もう一回
wight_decay:10^-6-10^-8
lr:0.01-0.001
Best-1(val acc:0.84) | lr:0.00971135118325034, weight decay:1.0394539789935165e-07
Best-2(val acc:0.83) | lr:0.009584343636422769, weight decay:3.1009381429608424e-07
Best-3(val acc:0.8) | lr:0.00832916652339643, weight decay:6.618592237280191e-07
Best-4(val acc:0.8) | lr:0.00959218016681805, weight decay:1.6405007969017657e-07
Best-5(val acc:0.78) | lr:0.006451172600874767, weight decay:4.0323875599954127e-07
Best-6(val acc:0.77) | lr:0.008024291255610844, weight decay:2.0050763243482884e-07
Best-7(val acc:0.77) | lr:0.009809009860349643, weight decay:4.934310445408953e-07
Best-8(val acc:0.77) | lr:0.009275309843754197, weight decay:5.343909279054936e-08
Best-9(val acc:0.76) | lr:0.00741122584285725, weight decay:1.588771824270857e-07
Best-10(val acc:0.75) | lr:0.006528687212003595, weight decay:1.3251120646717308e-07