40行でPoisson方程式を解く

こんにちは、やきつかです。
Haskellで配列を使ってみたいなーと思っていて、Poisson方程式を数値計算してみたら40行だったので1人で感動しちゃったので残しておきます。
Haskellの表現力の強さを知ってもらえればうれしいです。

#注意

• とりあえず実装したかったので、処理速度とかは一切考慮してないです。
• 同じ理由で、精度も可視化していい感じになることを目指しています。
• Haskell、数値計算とも初学者なので、間違いとかよりよい作法がありましたら教えていただけると大変うれしいです。

#はじめに
この記事では、Poisson方程式の概要→差分方程式→アルゴリズム→Haskellで書いたコードという順で説明していきます。

#Poisson方程式とは
Poisson方程式は二階の偏微分方程式で、次の様に表されるもののことを言います。

$$\Delta\phi=f$$

ここで、$\Delta$は微分演算子で

\Delta=\nabla \cdot \nabla \\
\nabla=(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z})

となります。また、$\phi,f$はスカラー関数です。

この記事では簡単のため二次元の系を扱うことにして、Poisson方程式として次の電位と電荷密度に関する方程式を解いてみます。3次元への拡張も簡単にできるので是非やってみて下さい。
$$\Delta\phi=-\frac{\rho}{\epsilon_0}$$

ただし、$\phi(x,y)$は座標$(x,y)$における電位、$\rho(x,y)$は電荷密度、$\epsilon_0$は真空中の誘電率を表します。

#差分方程式を導出する
解きたい方程式
$$\Delta\phi=-\frac{\rho}{\epsilon_0}$$

は次のようにも表せます。

$$\frac{\partial^2\phi}{\partial x^2}+\frac{\partial^2\phi}{\partial y^2}=-\frac{\rho}{\epsilon_0}$$

ここで、二階の偏導関数は格子幅$\Delta x$を用いて、

$$\frac{\partial^2\phi}{\partial x^2}\simeq\frac{\phi(x+\Delta x,y)-2\phi(x,y)+\phi(x-\Delta x,y)}{\Delta x ^2}$$

と近似できることが知られています。このような差分の取り方を中心差分と言います。
これを用いて偏導関数を置き換えると、次を得ます。
$$\frac{\phi(x+\Delta x,y)-2\phi(x,y)+\phi(x-\Delta x,y)}{\Delta x ^2} + \frac{\phi(x,y+\Delta y)-2\phi(x,y)+\phi(x,y-\Delta y)}{\Delta y ^2}=-\frac{\rho(x,y)}{\epsilon_0}$$
問題を簡単にするために、$\Delta x=\Delta y=\delta$として、$i,j\in\mathbb{Z},\phi(x+i\delta,y+j\delta)$を単に$\phi_{i,j}$と表記することにします。そうすると、次の差分方程式を得ます!

$$\phi_{i,j}=\frac{1}{4}(\phi_{i+1,j} + \phi_{i-1,j}+\phi_{i,j+1}+\phi_{i,j-1}+\delta^2\frac{\rho_{i,j}}{\epsilon_0})$$

つまり、ある一点$(i,j)$における電位$\phi_{i,j}$を求めるには周囲の4点での電位を平均した値に$\delta^2\frac{\rho_{i,j}}{4\epsilon_0}$を足せばよいと、この方程式は言っています。

#アルゴリズム
得られた差分方程式を用いて具体的に解く手法を考えます。

まず、対象とする$x,y$方向の区間を$n$分割し、格子幅を$δ$とします。すると$xy$平面は次のように分割されます。

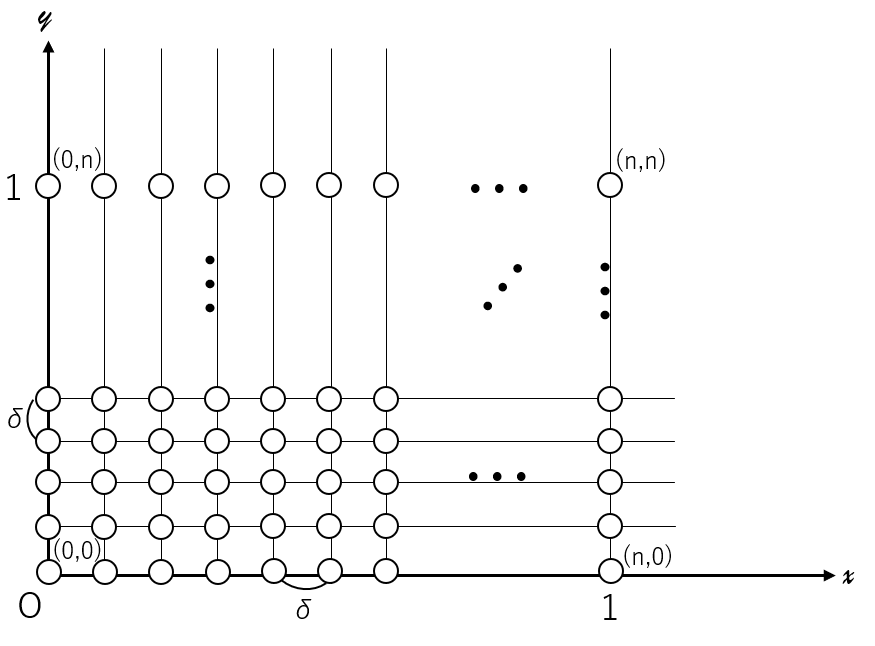
この場合、対象とする区間は$\forall x\in[0,1],\forall y\in[0,1]$です。
それぞれの点には物理量$\phi,\rho$がありこれらの値を差分方程式から求めれば良いのですが、$i=0,n$や$j=0,n$の時は周囲の値を参照することができないので、境界条件として

\forall i\forall j,\phi_{0,j}=\phi_{n,j}=\phi_{i,0}=\phi_{i,n}=0

を設けてやります。

そうすると、具体的には次のような連立方程式を解けば良いことになります。

\phi_{1,1}=\frac{1}{4}(\phi_{2,1} + \phi_{0,1}+\phi_{1,2}+\phi_{1,0}+\delta^2\frac{\rho_{1,1}}{\epsilon_0}) \\
\phi_{1,2}=\frac{1}{4}(\phi_{2,2} + \phi_{0,2}+\phi_{1,3}+\phi_{1,1}+\delta^2\frac{\rho_{1,2}}{\epsilon_0}) \\
\vdots \\
\phi_{n-1,n-1}=\frac{1}{4}(\phi_{n,n-1} + \phi_{n-2,n-1}+\phi_{n-1,n}+\phi_{n-1,n-2}+\delta^2\frac{\rho_{n-1,n-1}}{\epsilon_0})

しかし、実は困ったことに$\phi_{i,j} \ (1\le i\le n-1, 1\le j\le n-1)$の値も分からないのですが、上記の連立方程式はヤコビ法やガウス-ザイデル法と呼ばれる連立方程式の反復解法を用いることができる形になっています。(詳しくはヤコビ法を参照してください。)
今回はヤコビ法を用いることにして、適当に$\phi_{i,j}^{(0)}$の値を設定し、$\vec{x}^{(k+1)}=D^{-1}\lbrace\vec{b}-(L+U)\vec{x}^{(k)}\rbrace$という形の漸化式を上記の方程式に対して繰り返し適用し、
$$max \ |\phi_{i,j}^{(k+1)}-\phi_{i,j}^{(k)}|\lt\epsilon$$
という条件を満たした時、$\phi_{i,j}^{(k+1)}$を解として出力します。ただし、関数$max$は$i,j$の組み合わせを全て走査してその中の最大値を返す関数で、$\epsilon$は小さな数でプログラムの停止基準になります。

#問題設定
今回実際に数値計算してみる系として次のようなものを考えます。

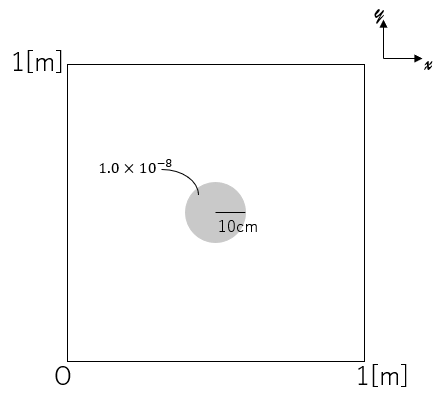
平面$1[m^2]$を対象として境界を含んで外側は接地されていて$0[V]$で、中心に半径$10[cm]$で電荷密度$1.0\times10^{-8}$の電荷を設置した状況で、各点の電位を求めます。

#Haskellプログラムの説明
それでは、Haskellでゴリゴリ書いていきましょう!
最初はもちろんライブラリのインポートです。

Haskell

module PoissonEqSolver where
import Data.Array
import Text.Printf

今回は主なデータ構造として配列を用いるのでData.Arrayを、出力する時に簡単に整形できるのでText.Printfをインポート
しています。(Arrayはboxedでimmutableな配列です。)

続いて、定数たちを宣言します。

Haskell

ε0 = 8.85E-12 --真空中の誘電率
n = 100 --区間はn分割される
δ = 1 / fromIntegral n --格子幅

上から、真空中の誘電率、分割数、格子幅です。

ところで、Haskellの配列はarray関数を用いて次の形で宣言します。

Haskell

arr = array (インデックスの最小値,インデックスの最大値) [(インデックス,要素) | インデックスの生成]

arrの型はArray i eでiはインデックスの型、eは要素の型となります。
ちなみに、インデックスへのアクセスは!関数でやります。
これを使って仮の電位分布と電荷分布を二次元配列で宣言します。

Haskell

φ0 :: Array (Int, Int) Double
φ0 = array ((0,0),(n,n)) [((x,y), 0) | x <- [0..n], y <- [0..n]] --仮の電位分布

ρ0 :: Array (Int, Int) Double
ρ0 = array ((0,0),(n,n)) [((x,y), f x y) | x <- [0..n], y <- [0..n]] --電荷密度の分布
    where
        f x y | (δ*fromIntegral (x - div n 2))^2 + (δ*fromIntegral (y - div n 2))^2 <= 0.1^2 = 1.0E-08 --円状に電荷密度を分布させる
              | otherwise = 0

仮の電位分布φ0は全ての要素を0にセットしておいて、電荷分布ρ0には中心に円状に電荷を分布をさせています。(fromIntegral関数を多用するとコードが汚くなっちゃうのはしょうがないのでしょうか...?)

それでは、漸化式を記述する関数nextを実装します。

Haskell

next :: Array (Int, Int) Double -> Array (Int, Int) Double -> Array (Int, Int) Double
next ρ φ = φ // [((x,y),f x y) | x <- [1..n-1], y <- [1..n-1]]
    where
        f x y  = (/4) $ φ ! (x+1,y) + φ ! (x-1,y) + φ ! (x,y+1) + φ ! (x,y-1) + δ^2 * ρ ! (x,y) / ε0

where句で宣言されている関数fはインデックスx,yから周囲の物理量にアクセスして平均した値を返します。fをインデックス全体に渡ってmapしてあげることで次のステップの状態に移ります。

得られた電位をgnuplotで表示できるように、雑に外部出力関数を作ります。

haskell

output :: Array (Int,Int) Double -> IO ()
output φ = do
    let filePath = "./result.dat"
    writeFile filePath ""
    mapM_ (appendFile filePath) $ do
        x <- [0..n]
        y <- [0..n]
        return $ printf "%d %d %.15f\n" x y (φ ! (x,y))

filePathに出力先のパスを宣言、writeFile関数でとりあえずファイルを開きます。
その後、mapM_でリスト全体にappend関数を適用することで、filePathにx y φ(x,y)の順で逐次書き込みます。(初めてリストモナドを使ってみました、かっこいいですね。)

最後に、実際に系を解く関数を用意しておしまいです。

Haskell

solve :: Double -> Array (Int,Int) Double -> Array (Int,Int) Double -> IO ()
solve ε ρ φ | error < ε = do
                putStrLn "Write result to ./result.dat \nWait..."
                output φ'
                printf "Finished.\n"
            | otherwise = solve ε ρ φ'
    where
        φ' = next ρ φ
        error = maximum [abs ( φ ! (x,y) - φ' ! (x,y) ) | x <- [0..n], y <- [0..n]]

この関数を端的に説明すると、現時点での解と後の解との誤差をerrorで評価してε未満ならば、output関数に電位を渡す、そうでなければ、次のステップの電位を自身に引数として渡す、ということをします。where句では、次のステップの電位であるφ'と誤差errorが定義されています。

#40行でPoisson方程式を解く
まとめとして、ソースコード全体を載せておきます。ぴったり40行だよ、やったね!

Haskell

module PoissonEqSolver where
import Data.Array
import Text.Printf

ε0 = 8.85E-12 --真空中の誘電率
n = 100 --区間はn分割される
δ = 1 / fromIntegral n --格子幅

φ0 :: Array (Int, Int) Double
φ0 = array ((0,0),(n,n)) [((x,y), 0) | x <- [0..n], y <- [0..n]] --仮の電位分布

ρ0 :: Array (Int, Int) Double
ρ0 = array ((0,0),(n,n)) [((x,y), f x y) | x <- [0..n], y <- [0..n]] --電荷密度の分布
    where
        f x y | (δ*fromIntegral (x - div n 2))^2 + (δ*fromIntegral (y - div n 2))^2 <= 0.1^2 = 1.0E-08 --円状に電荷密度を分布させる
              | otherwise = 0

next :: Array (Int, Int) Double -> Array (Int, Int) Double -> Array (Int, Int) Double
next ρ φ = φ // [((x,y),f x y) | x <- [1..n-1], y <- [1..n-1]]
    where
        f x y  = (/4) $ φ ! (x+1,y) + φ ! (x-1,y) + φ ! (x,y+1) + φ ! (x,y-1) + δ^2 * ρ ! (x,y) / ε0

output :: Array (Int,Int) Double -> IO ()
output φ = do
    let filePath = "./result.dat"
    writeFile filePath ""
    mapM_ (appendFile filePath) $ do
        x <- [0..n]
        y <- [0..n]
        return $ printf "%d %d %.15f\n" x y (φ ! (x,y))

solve :: Double -> Array (Int,Int) Double -> Array (Int,Int) Double -> IO ()
solve ε ρ φ | error < ε = do
                putStrLn "Write result to ./result.dat \nWait..."
                output φ'
                printf "Finished.\n"
            | otherwise = solve ε ρ φ'
    where
        φ' = next ρ φ
        error = maximum [abs ( φ ! (x,y) - φ' ! (x,y) ) | x <- [0..n], y <- [0..n]]

Haskellは楽しい!

#gnuplotで表示する
ghciでsolve 1e-05 ρ0 φ0を入力しEnterキーを押して待ちます。
result.datが吐き出されます。

出力されたresult.datをgnuplotで可視化してみました。z軸が電位[V]の大きさを表しています。

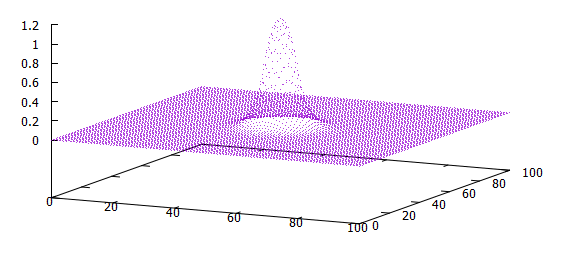
いい感じですね。

#感想
今回は配列を用いてPoisson方程式を解いてみました、楽しかったです。
ただ、想像以上に処理に時間がかかり、如何にして速度を出すかが課題だと思いました。(IOUArrayでSOR法で解いてみたい、Vectorが早いと風のうわさで聞いたので使ってみたい。)
本当は解析解との比較などもやりたかったのですが、それは他の強い文献にまかせて自粛させていただきます。

ここまで見てくれた人、ありがとうございます!

#最後に
PoissonがPoisonになってないかめっちゃ確認しました。