こんにちは、趣味でHaskellを勉強している者です。
はじめに
Haskellで超絶手軽にグラフィック描画ができるgloss、いいですよね。
glossについては、超絶わかりやく解説されている記事があるので、そちらを!glossではじめるグラフィック描画 :: Haskell入門の次に読む記事
glossは超絶使いやすい神ライブラリなのですが、二次元波動方程式のシミュレーションをしようとして、僕はふと思ってしまったんです。
「glossじゃ3D描画無理くない?」
それで、Hackageで色々探しているとnot-glossというパッケージがありまして...
このnot-gloss、glossをそのまま3D描画に対応させたって感じで使いやすかったんですよね。中身はgolssとほぼ同じ使い方ができるOpenGLのラッパーです。
そして、なぜか日本語で解説されてる記事がなかったので、頑張って書きました。
not-glossをインストールしよう
適当にプロジェクトを作って、次のコマンドを打つだけです。
$ stack install not-gloss
$ stack build
ちょっと時間がかかるかもしれません、辛抱しましょう。
終わったら、package.yamlに依存関係としてnot-glossとlinearを追加しておきましょう。linearは三次元座標を扱うのに用います。
こんな感じです。
dependencies:
- base >= 4.7 && < 5
- not-gloss
- linear
立方体を表示する
せっかくなので、何か表示しましょう。Main.hsで次のように記述して、
module Main where
import Vis
import Linear.V3
main :: IO ()
main = display defaultOpts (Cube 0.5 Solid blue)
stack runするだけでOK
not-glossの基本
not-glossにはdisplay,animate,simulate,playという描画の目的別に関数が用意されています。ここでは、これらの関数の簡単な使い方をご紹介します。
display
display関数は、動かないオブジェクトを描画するだけの単純明快な関数です。
display :: Real b
=> Options -- ^ 設定
-> VisObject b -- ^ オブジェクト
-> IO ()
glossと違うポイントは、Options型にウィンドウサイズや背景色、初期カメラ位置などの情報が格納されている点です。Real b => VisObject bは、描画されるオブジェクトのことであり、立方体や球、3Dテキストなど色々ありますが、後述します。
Options型には、defaultOptsというデフォルト設定があらかじめ用意されています。Options型はレコードになっているので、次のようにすることで部分的に変更することができます。
main :: IO ()
main = display myOpts (Cube 0.5 Solid blue)
myOpts = defaultOpts { optBackgroundColor = Just white }
このように、部分的にoptBackgroundColorの値を変更することで、背景の色を変えることができます!
OptionsとVisObjectについては記事後半を参照してください!
animate
animate関数はオブジェクトの時間変化によるシンプルな描画を行う関数です。
animate :: Real b
=> Options -- ^ オプション
-> (Float -> VisObject b) -- ^ 時刻を受け取って、オブジェクトを生成する関数
-> IO ()
試しに、立方体をどんどん大きくする描画をしてみましょう。
main :: IO ()
main = animate defaultOpts (\t -> Cube t Solid white)
animateの第二引数に時刻tを受け取ってVisObjectを返す関数を渡してあげます。これを実行すると、次のようになります。
簡単に3Dアニメーションの描画ができます。
simulate
simulate関数は初期状態、状態を引数にしてオブジェクトを描画する関数、状態を更新する関数から状態の時間発展を描画する関数です。ここで登場する状態は既存の型でもいいですし、自作の代数的データ型でもなんでもOKです。
simulate :: Real b
=> Options
-> Double -- ^ サンプルレート
-> world -- ^ 初期状態
-> (world -> VisObject b) -- ^ 状態を描画する関数
-> (Float -> world -> world) -- ^ 前ステップからの経過時間、前の状態から次の状態を作る関数
-> IO ()
シミュレーションの例としてN体運動もどきを作ってみます。
状態を、質量・位置・速度を持つデータ型の集まりとします。
import qualified Data.Vector as V
data Body = Body
{
position :: V3 Float -- 位置
, velocity :: V3 Float -- 速度
} deriving Show
type Bodies = V.Vector Body -- データ型の集まり
ここで、初期状態を用意しておきましょう。
initBodies :: Bodies
initBodies = V.fromList
[
Body (V3 (-1) 0 0) (V3 0 0 0)
, Body (V3 0 0 1) (V3 0 0 0)
, Body (V3 0 0 0) (V3 0 0 0)
, Body (V3 0 1 0) (V3 0 0 0)
]
次に、この状態を描画する関数を作ります。
drawBodies :: Bodies -> VisObject Float
drawBodies bodies =
let
drawBody body = Trans (position body) $ Sphere 0.1 Solid white
in
VisObjects $ V.toList $ V.map drawBody bodies
ここで、TransはLinear.V3型の位置とオブジェクトを引数に、オブジェクトをその位置に移動させる関数です。glossのtranslateと同じです。
位置を参照してその場所に球体を表示させているだけです!
そして、最後に状態を更新する関数を用意。
nextBodies :: Float -> Bodies -> Bodies
nextBodies dt bodies = (`V.imap` bodies) $ \i _ ->
let
_G = 6.67408E-11 -- 万有引力定数
ε = 0.15 -- ソフトニングパラメータ
scalar x = V3 x x x -- スカラー値をベクトルにする関数
xᵢ = position (bodies V.! i) -- i番目の質点の位置
vᵢ = velocity (bodies V.! i) -- i番目の質点の速度
exceptme = V.ifilter (\j _ -> j /= i) bodies
vᵢ' = vᵢ + scalar (dt * _G) * V.sum ( V.map (\body -> (position body - xᵢ) / scalar ( (norm (position body - xᵢ)^2 + ε^2)**1.5 ) ) $ exceptme )
xᵢ' = xᵢ + scalar dt * vᵢ'
in
Body mᵢ xᵢ' vᵢ'
あとはできあがったパーツをはめるだけ。
main :: IO ()
main = simulate defaultOpts (1/60) initBodies drawBodies nextBodies
simulate関数を使えば手軽に3次元シミュレーションができます。
play
キーボードやマウスによって発生するイベントで描画をコントロールできる関数です。
play :: Real b
=> Options -- ^ オプション
-> Double -- ^ サンプル時間
-> world -- ^ 初期状態
-> (world -> (VisObject b, Maybe Cursor)) -- ^ 状態の描画
-> (Float -> world -> world) -- ^ 状態の更新
-> (world -> IO ()) -- ^ カメラのセット
-> Maybe (world -> Key -> KeyState -> Modifiers -> Position -> world) -- ^ キーボード/マウスのボタンのコールバック
-> Maybe (world -> Position -> world) -- ^ マウスドラッグのコールバック
-> Maybe (world -> Position -> world) -- ^ マウスを動かしたときのコールバック
-> IO ()
not-gloss開発者のexampleを載せておきます。
{-# OPTIONS_GHC -Wall #-}
module Main ( main
) where
import Linear ( V3(..), (*^) )
import qualified Data.Set as Set
import Graphics.X11 ( initThreads )
import Graphics.UI.GLUT ( Cursor(..), Key(..), KeyState(..), Modifiers(..), Position(..)
, Size(..), Vector3(..), Vertex3(..)
, GLint
, ($=)
)
import qualified Graphics.UI.GLUT as GLUT
import SpatialMath ( Euler(..), rotateXyzAboutZ, rotVecByEulerB2A )
import Vis
import Control.Monad ( when )
ts :: Double
ts = 0.01
faceHeight :: Double
faceHeight = 1.5
data PlayerState = Running (V3 Double) (V3 Double) (Euler Double)
data GameState = GameState { playerState :: PlayerState
, keySet :: Set.Set Key
, lastMousePos :: Maybe (GLint,GLint)
}
toVertex :: (Real a, Fractional b) => V3 a -> Vertex3 b
toVertex xyz = (\(V3 x y z) -> Vertex3 x y z) $ fmap realToFrac xyz
setCamera :: PlayerState -> IO ()
setCamera (Running (V3 x y z) _ euler) =
GLUT.lookAt (toVertex xyz0) (toVertex target) (Vector3 0 0 (-1))
where
xyz0 = V3 x y (z-faceHeight)
target = xyz0 + rotVecByEulerB2A euler (V3 1 0 0)
simfun :: Float -> GameState -> IO GameState
simfun _ (GameState (Running pos _ euler0@(Euler yaw _ _)) keys lmp) = do
Size x y <- GLUT.get GLUT.windowSize
let x' = (fromIntegral x) `div` 2
y' = (fromIntegral y) `div` 2
when (Just (x',y') /= lmp) (GLUT.pointerPosition $= (Position x' y'))
return $ GameState (Running (pos + (ts *^ v)) v euler0) keys (Just (x',y'))
where
v = rotateXyzAboutZ (V3 (w-s) (d-a) 0) yaw
where
w = if Set.member (Char 'w') keys then 3 else 0
a = if Set.member (Char 'a') keys then 3 else 0
s = if Set.member (Char 's') keys then 3 else 0
d = if Set.member (Char 'd') keys then 3 else 0
keyMouseCallback :: GameState -> Key -> KeyState -> Modifiers -> Position -> GameState
keyMouseCallback state0 key keystate _ _
| keystate == Down = state0 {keySet = Set.insert key (keySet state0)}
| keystate == Up = state0 {keySet = Set.delete key (keySet state0)}
| otherwise = state0
motionCallback :: Bool -> GameState -> Position -> GameState
motionCallback _ state0@(GameState (Running pos v (Euler yaw0 pitch0 _)) _ lmp) (Position x y) =
state0 {playerState = newPlayerState, lastMousePos = Just (x,y)}
where
(x0,y0) = case lmp of Nothing -> (x,y)
Just (x0',y0') -> (x0',y0')
newPlayerState = Running pos v (Euler yaw pitch 0)
dx = 0.002*realToFrac (x - x0)
dy = 0.002*realToFrac (y - y0)
yaw = yaw0 + dx
pitch = bound (-89) 89 (pitch0 - dy)
bound min' max' val
| val < min' = min'
| val > max' = max'
| otherwise = val
drawfun :: GameState -> VisObject Double
drawfun (GameState (Running _ _ _) _ _) =
VisObjects $ [axes,box,ellipsoid,sphere] ++ (map text [-5..5]) ++ [boxText, plane]
where
x' = -1
axes = Axes (0.5, 15)
sphere = Trans (V3 0 x' (-1)) $ Sphere 0.15 Wireframe (makeColor 0.2 0.3 0.8 1)
ellipsoid = Trans (V3 x' 0 (-1)) $ Ellipsoid (0.2, 0.3, 0.4) Solid (makeColor 1 0.3 0.5 1)
box = Trans (V3 0 0 x') $ Box (0.2, 0.2, 0.2) Wireframe (makeColor 0 1 1 1)
plane = Plane (V3 0 0 1) (makeColor 1 1 1 1) (makeColor 0.4 0.6 0.65 0.4)
text k = Text2d "OLOLOLOLOLO" (100,500 - k*100*x') TimesRoman24 (makeColor 0 (0.5 + x''/2) (0.5 - x''/2) 1)
where
x'' = realToFrac $ (x' + 1)/0.4*k/5
boxText = Text3d "trololololo" (V3 0 0 (x'-0.2)) TimesRoman24 (makeColor 1 0 0 1)
main :: IO ()
main = do
let state0 = GameState (Running (V3 (-2) 0 0) 0 (Euler 0 0 0)) (Set.empty) Nothing
setCam (GameState x _ _) = setCamera x
drawfun' x = return (drawfun x, Just None)
_ <- initThreads
playIO (defaultOpts {optWindowName = "play test"}) ts state0 drawfun' simfun setCam
(Just keyMouseCallback) (Just (motionCallback True)) (Just (motionCallback False))
playを使えば簡単にインタラクティブな描画を実現できます。
Options
Options型は次のように定義されています。
Options = Options
{
optBackgroundColor :: Maybe Color -- ^ 背景色
, optWindowSize :: Maybe (Int, Int) -- ^ ウィンドウサイズ, Just (横のピクセル, 縦のピクセル) で指定
, optWindowPosition :: Maybe (Int, Int) -- ^ ウィンドウを表示する位置, Just (横のピクセル, 縦のピクセル) で指定
, optWindowName :: String -- ^ ウィンドウ名, 文字列を与えて指定
, optInitialCamera :: Maybe Camera0 -- ^ カメラの初期位置, Camera0型の値を与えて指定
, optAnitialiasing :: Antialiasing -- ^ アンチエイリアスをどうするか, Anitialiasing型の値で指定
}
なぜ、Maybeで包まれてるかはよくわからないのですが、とりあえずJustでくるんで渡せば大丈夫です。(Nothingはデフォルト値を返すっぽい?)
Camera0
Camera0は描画のスタートにおけるカメラの向きの情報を持ちます。
data Camera0 =
{
phi0 :: GLDouble
, theta0 :: GLDouble
, rho0 :: GLDouble
}
ここで、GLDoubleはDoubleのエイリアスなので、そのまま数値を指定すれば大丈夫です。
3つの角度$\phi,\theta,\rho$をそれぞれ指定してあげることで、初期のカメラ向きを決定できます。
main = display myOpts (Cube 0.5 Solid white)
where
myOpts = defaultOpts { optInitialCamera = Camera0 { phi0 = pi/2 } }
Antialiasing
アンチエイリアスをどうするかを決定できるパラメータです。(アンチエイリアスは、デジタルで描画する時に発生するジャギジャギをなめらかにすることで、違和感を抑える処理だと思ってください。)
data Antialiasing = Aliased -- ^ エイリアスを除かない
| Smoothed -- ^ スムージングする
| Multisampled Int -- ^ マルチサンプリングする
こんな感じで指定します。
main = display myOpts (Cube 0.5 Solid white)
where
myOpts = defaultOpts { optAnitialiasing = Smoothed }
VisObject
VisObjectは描画できるオブジェクトと、オブジェクトへの作用からなり、様々なものが用意されています。
data VisObject a =
-- 作用系
VisObjects [VisObject a] -- ^ 複数のオブジェクトをひとつにする
Trans (V3 a) (VisObject a) -- ^ オブジェクトを移動させる
RotQuot (Quaternion a ) (VisObject a) -- ^ クォータニオンによる回転作用
RotDcm (M33 a) (VisObject a ) -- ^ 回転行列による回転作用
RotEulerDeg (Euler a) (VisObject a) -- ^ オイラー角による回転作用 (度)
RotEulerRad (Euler a) (VisObject a) -- ^ オイラー角による回転作用 (ラジアン)
Scale (a, a, a) (VisObject a) -- ^ オブジェクトを拡大
-- オブジェクト
Cylinder (a, a) Color -- ^ 円筒
Box (a, a, a) Flavour Color -- ^ 直方体
Cube a Flavour Color -- ^ 立方体
Sphere a Flavour Color -- ^ 球
Ellipsoid (a, a, a) Flavour Color -- ^ 楕円体
Line Maybe a [V3 a] Color -- ^ 線
Line' Maybe a [(V3 a, Color)] -- ^ 線
Arrow (a, a) (V3 a) Color -- ^ 矢印
Axes (a, a) -- ^ 軸
Plane (V3 a) Color Color -- ^ 平面
Triangle (V3 a) (V3 a) (V3 a) Color -- ^ 三角形
Quad (V3 a) (V3 a) (V3 a) (V3 a) Color -- ^ 四角形
Text2d String (a, a) BitmapFont Color -- ^ 2dテキスト
Text3d String (V3 a) BitmapFont Color -- ^ 3dテキスト
Points [V3 a] (Maybe GLfloat) Color -- ^ 点群
オブジェクトのFlavourには描画方法(メッシュor塗りつぶし)を指定、Colorには色を指定します。
GLfloatはfloatのエイリアスです。
Flavour
Flavourは2値からなる型で、オブジェクトをどのように描画するか指定します。
Flavour = Solid -- ^ 塗りつぶし
| Wireframe -- ^ メッシュ
違いはこんな感じ
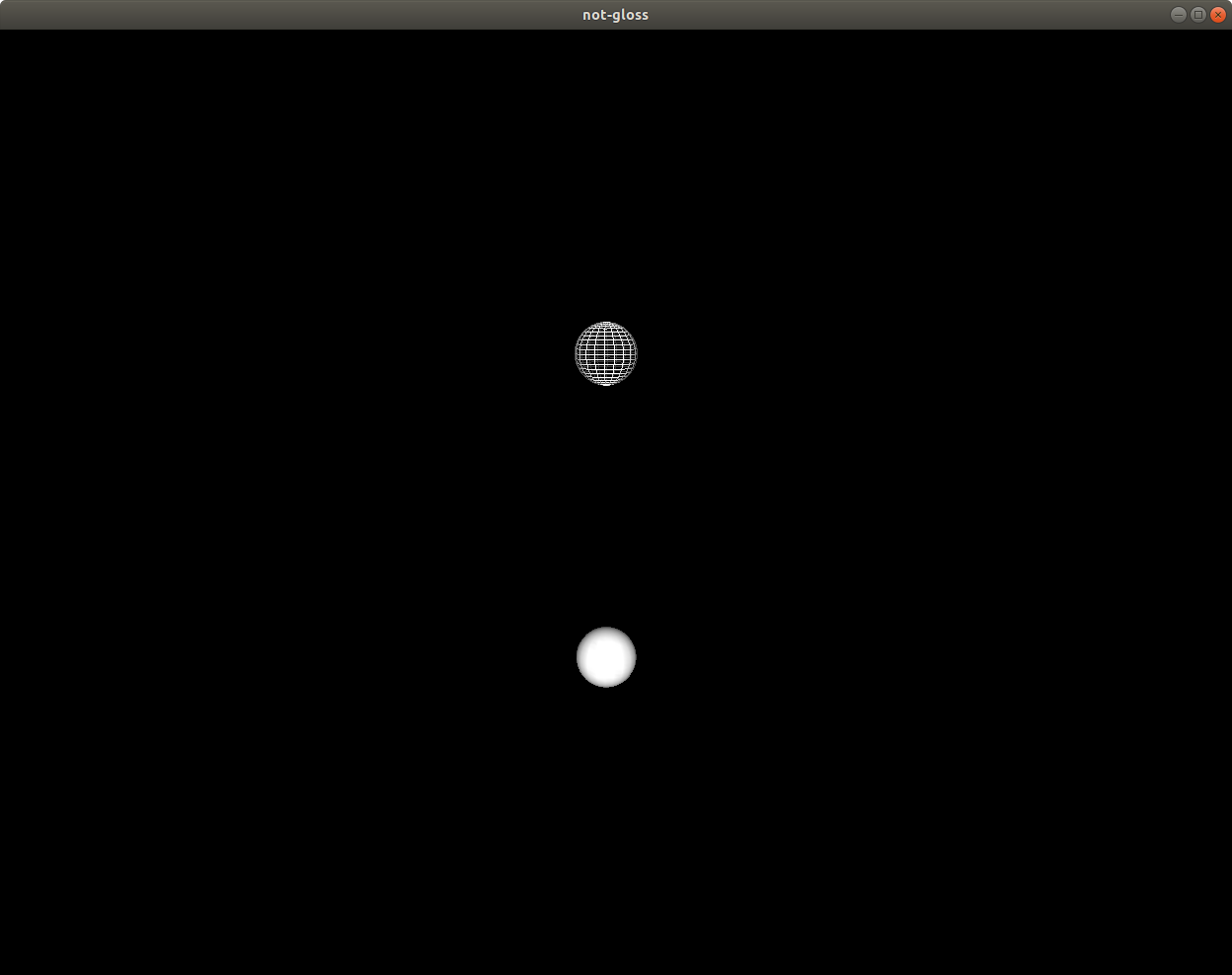
上がWireframeで下がSolidです。お好みな方を使いましょう。
Color
色を作る関数が用意されています。
makeColor :: Float -- ^ R
-> Float -- ^ G
-> Float -- ^ B
-> Float -- ^ α
-> Color
R,G,B,αの値は[0..1]の範囲で指定します。
makeColor8関数を使えば[0..255]のInt値でも指定できます。
また、定義済みの色は次の通り。
- 基本
- `black`, `white`
- 主要な色
- `red`, `green`, `blue`
- 二次的な色
- `yellow`, `cyan`, `magenta`
- より複合的な色
- `rose`, `violet`, `azure`, `aquamarine`, `chartreuse`, `orange`
また、mixColors関数を使えば色を混ぜることができます。
mixColors :: Float -- ^ 1つ目の色の比率
-> Float -- ^ 2つ目の色の比率
-> Color -- ^ 1つ目の色
-> Color -- ^ 2つ目の色
-> Color
light関数やdark関数を使うことで色を明るくしたり暗くしたりすることも可能です。詳しくはココを参考にしてください。
BitmapFont
Text2DやText3Dを描画する際に、フォントを指定することができます。
data BitmapFont = Fixed8By13
| Fixed9By15
| TimesRoman10
| TimesRoman24
| Helvetica10
| Helvetica12
| Helvetica18
後ろの数字はポイントサイズです。僕はTimesRomanが好きです。
main = display defaultOpts (Text3D "Hello, Haskeller!" (V3 1 1 1) TimesRoman10 rose)
おわりに
not-glossを使えば、OpenGLを使いこなせるように修行せずとも簡単に3Dグラフィック描画が可能です。
「頭使わずに可視化したいな...」、「ちょっとした3Dゲームを作ってみたいな...」という願望がある方はすぐに試してみましょう!
ここまで見てくださった方、ありがとうございました〜