【読書メモ】図解これならわかるベイズ統計学

読書メモとして投稿させていただきます。
間違え等ありましたら申し訳ございません。

1章 ベイズ理論の考え方

• ベイズの定理

  $$
  P(A|B) = \frac{P(B|A)P(A)}{P(B)}
  $$

  • この式を出発点として考えていく
  • A,Bをいろいろに解釈する
  • Aを原因、Bをデータと解釈すると、ベイズ確率論の基本公式となる
  • ベイジアンネットワーク：事象の推移を確率的に計算する論理をモデル化したもの
  • Aを確率分布、Bをデータと解釈すると、ベイズ統計論
  • 曖昧性や不厳密性を許容することにより柔軟性がある
  • 人間の感性に近い、経験や常識を取り込んだデータ処理も可能
  • 事前確率：最初に設定した確率（常識的にとりあえず仮定する確率）。主観確率とも呼ばれる
  • 事後確率：事前確率にデータを加味したもの
  • ベイズ更新：データを取りこむたびに事後確率が変化すること
  • 前の確率（事前確率）にデータを取り込んで新たな確率（事後確率）を算出する

• 従来の統計学とベイズ統計学の違い

  従来の統計学

  1. 定まった母集団の平均（母平均）で規定される確率分布に従うと仮定する
  2. たまたま選び出した標本の平均値を標本平均と呼ぶ
  3. 何回も標本をランダムに選び出せば、そこから得られる標本平均はいろいろと変化するが母平均で規定される確率分布に従う
  • この発想と確率論を組み合わせることで、従来の統計学は母平均の推定や検定を行う
  • 頻度論と呼ぶ
  • データをたくさんある中の1つとして扱う
  • 母数（パラメータ）は母集団固有の唯一の値を仮定する

  ベイズ統計学

  1. 母集団の平均（母平均）で規定される確率分布に従うと仮定する
  2. 今得られたデータを唯一のデータとして扱う
  3. そのデータを利用して、仮定した確率分布から母集団の平均の分布を算出
  • データを一期一会的に扱う
  • 母数は確率変数であり、その分布を調べようとする
  • 母数（パラメータ）：データが従う確率分布を決定する定数のこと
    • 平均値や分散など

2章 ベイズ理論のための確率入門

• 試行：さいころを投げること

• 事象：得られた結果

• 標本空間：起こりえるすべての場合

• 統計的確率（割合）：何回も繰り返した時に得られる事象の割合

• 数学的確率

  $$
  P(A) = \frac{n(A)}{n(S)}
  $$

  • n(S)は標本空間

• 2つの事象が同時に起こる確率を同時確率

• 条件付き確率：事象Bを全体と考えたときに事象B の起こる確率

  $$
  P(A|B) = \frac{P(A \cap B)}{P(B)}
  $$

• 確率の乗法定理

  $$
  P(A \cap B) = P(A)P(B|A) \quad \text{または} \quad P(A \cap B) = P(B)P(A|B)
  $$

• 事象の独立

  • A,Bが関係しなければ、Aが起ころうと起こるまいとBの起こる確率には関係ないその状況を独立。関係があるとき従属。

• 独立事象の乗法定理

  $$
  P(A \cap B) = P(A)P(B)
  $$

• 確率変数：確率的に値の決まる変数

  • さいころの出目など、さいころが投げ終わらないと値が確定しない

• 確率変数のとる各値に対応して、それらが起こる確率が与えられるときその対応を確率分布という

• 確率変数と確率分布が与えられた時、平均値と分散、標準偏差が考えられる

  • 平均値とは確率変数における並みの値を、分散とは平均値からの散らばり具合を表現する値
  • 平均値は期待値とも呼ばれる

• 確率変数の平均は

  $$
  E(X) = \sum_{i} x_i P(X = x_i) \quad \text{(離散確率変数の場合)}
  $$

• 確率変数の分散は

  $$
  \text{Var}(X) = E[(X - E(X))^2] = \sum_{i} (x_i - E(X))^2 P(X = x_i) \quad \text{(離散確率変数の場合)}
  $$

• 確率変数の標準偏差は

  $$
  \sigma(X) = \sqrt{\text{Var}(X)}
  $$

  • 平均値は確率変数の分布の重心、標準偏差は平均値からの散らばりの幅の目安

3章 ベイズの定理の基本

• ベイズの定理（乗法公式から導出）

  $$
  P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}
  $$

  $$
  \text{BのもとでAが起こる確率} = \frac{\text{AのもとでBが起こる確率} \cdot \text{Aの起こる確率}}{\text{Bの起こる確率}}
  $$

  ベイズの定理の見方

  • P(B|A)をP(A|B)に変換している式と考えられる
  • ベイズの定理は、条件付き確率の役割を逆さに変換する
  • P(A|B)をP(B|A)の逆確率

  他の見方

  • 何も条件がない時にAが起こる確率P(A)を、Bの下でAの起こる確率P(A|B)に変換している。
  • Bの条件がどれくらいAに影響するかを定量的に与える
  • Bをデータと解釈するなら、データ取得前と後との確率の関係を示している
  • P(A)を事前確率、P(A|B)を事後確率

• ベイズの定理を解釈し直すとベイズの基本公式

  $$
  P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)}
  $$

  • H：原因
  • D：データ
  • 一般的には、原因が与えられた時にその結果を議論する
  • しかし、それを反対にし、結果から原因をたどれるように変換してくれる
    • データが与えられた時に原因を求める確率を表している
  • P(H|D)をデータDの原因の確率

• 現実世界では原因がいくつも考えられるのが普通

  

  $$
  P(H_i|D) = \frac{P(D|H_i) \cdot P(H_i)}{P(D)}(i=1,2,...,n)
  $$

• ベイズの展開公式

  • 3つの原因にダブりはない(排反である)とする

  $$
  P(D)=P(D\cap H_1)+P(D\cap H_2)+P(D\cap H_3)
  $$

  $$
  P(H_1|D) =
  \frac{P(D|H_1) \cdot P(H_1)}
  {P(D|H_1)P(H_1)+P(D|H_2)P(H_2)+P(D|H_3)P(H_3)}
  $$

  • 一般的な式は以下

  $$
  P(H_i|D) = \frac{P(D|H_i) \cdot P(H_i)}{\sum_{j=1}^{n} P(D|H_j) \cdot P(H_j)}
  $$

  • 事後確率 P(Hi | D)：データDが原因Hiから得られた確率
  • 尤度 P(D | Hi)：原因Hiの下でデータDが得られる確率
    • 尤度の合計が1になる必要はない
  • 事前確率P(Hi)：データDを得る前の原因Hiの確からしさ
    • 事前確率の総和は必ず1になる
  • ベイズの展開公式の本質は、事後確率が尤度と事前確率の積に比例すること
  • ベイズ理論の計算は3ステップ
    1. モデル化し、それから尤度を算出
    2. 事前確率を設定
    3. ベイズの展開公式を用いて事後確率を算出
  • 理由不十分の原則：何の情報もなければ確率は同等という発想
    • 人間の常識をあえて確率計算に取り入れる
  • ベイズ更新：前回の事後確率を今回の事前確率として利用すること
    • ベイズ更新は学習：データを取り入れて確度を変更するという過程は、人間の学習動作（人の推理）に似ている
    • ベイズ更新という武器を利用して、データを得るたびに処理を進めるのがベイズ流データ処理
    • 事前確率や事後確率を信念と呼ぶこともある。ベイズ理論は心の確信度も扱うことができ、このような確率を一般的に主観確率と呼ぶ
  • ベイズ更新による逐次合理性
    • ベイズ理論は、独立した複数のデータを1つずつ処理できるという便利な特徴がある。
    • しかし、「データを取り込む順番で結果が異なってしますのでは？？」
      ⇒その心配はいらない
  • 逐次合理性：データが同じであれば解析順序に依らない

4章 ベイズ理論の応用

• ベイズ理論による推定法のメリット

  • 事前確率に前のデータも取り込めること

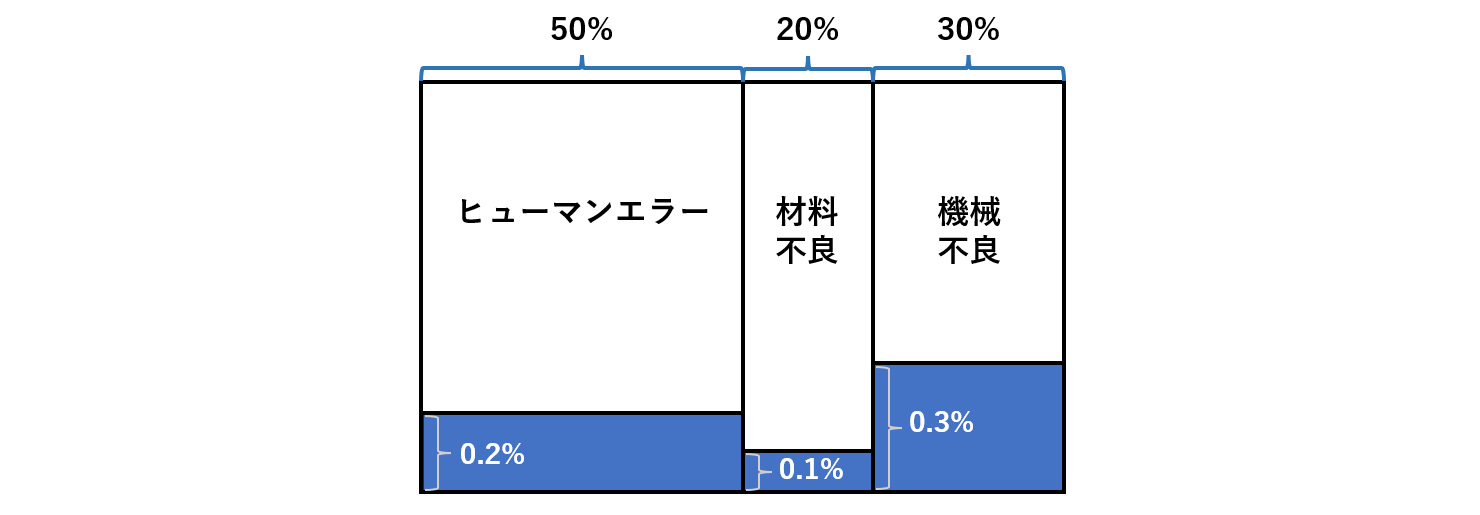
• 基準率の無視：事前確率を忘れてしまう事。ひとは事前確率に鈍感

  • 確率計算が常識に反した意外な結果になるとき、多くの場合は事前確率が関係する

• ナイーブベイズ分類：ベイズ理論を利用して、与えられたデータを目的のカテゴリーに分類する方法。文書分類などに利用される

  • ナイーブ：単語間の関係を無視し独立して判定する単純なモデル

• 確率分布をベイズ推定

  • MAP推定：事後確率が最大の原因を真の原因と推定する方法
  • 最尤推定法：尤度が一番大きいことが一番よく起こる
    • 推定には常識が重要：推定の大きな要素を占めるのは事前確率

• 世の中の現象の多くは確率の連鎖。原因と結果の連鎖。

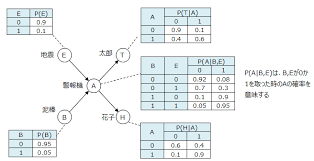
• ベイジアンネットワーク

  

  • マルコフ条件：各ノードの確率変数は、そのノードの親ノードの条件付確率のみで表される

5章 ベイズ統計学のための準備

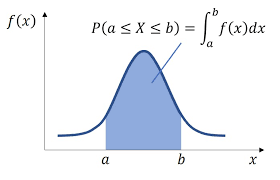
• 確率密度関数：連続的な確率変数の分布

  • z常に幅を持って議論する

  

  • 平均値（期待値）

  $$
  E(X) = \int_{a}^{b} x f(x) , dx
  $$

  • 分散

  $$
  Var(X) = \int_{a}^{b} (x - E(X))^2 f(x) , dx

  $$

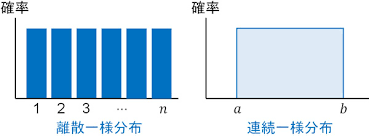
• 一様分布：確率変数xのどんな値に対しても、それが起こる確率値が同じである確率分布

  • 連続型と離散型がある

  

  • 一様分布の確率密度関数

  $$
  f(x) = \begin{cases} \frac{1}{b - a} & \text{for } a \leq x \leq b \0 & \text{otherwise}\end{cases}
  $$

  • 平均（期待値）

  $$
  E(X) = \frac{a + b}{2}
  $$

  • 分散

  $$
  Var(X) = \frac{(b - a)^2}{12}
  $$

• ベルヌーイ分布：コインの表裏のように事象が2つしかない試行をベルヌーイ試行という。そのベルヌーイ試行を記述する確率変数の分布がベルヌーイ分布。確率変数は0と1のみを値としてとる。

  

  X	確率
  0	1-p
  1	p

  • 平均値

  $$
  \mu =p
  $$

  • 分散

  $$
  \text{Var}(X) = p(1 - p)
  $$

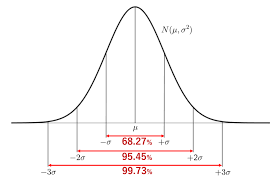
• 正規分布：統計学の代表的な分布。別名、誤差分布・ガウス分布

  $$
  N(\mu , \sigma^2)
  $$

  

  • 確率密度関数

  $$
  f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}
  $$

  • σは標準偏差、μは平均を表す
  • 中心極限定理：ある程度大きな個数について平均値を求めると、その分布は正規分布になる

• ベータ分布：自然な共役分布として使われる（ベータ関数）

  $$
  Be(p,q)
  $$

  

  • 確率密度関数（0<x<1）

  $$
  f(x)=kx^{p-1}(1-x)^{q-1}
  $$

  • 平均

  $$
  \mu = \frac{p}{p + q}

  $$

  • 分散

  $$
  \sigma^2 = \frac{p q}{(p + q)^2(p + q + 1)}
  $$

  • モード

  $$
  \text{Mode} = \frac{p - 1}{p + q - 2}
  $$

  • 比例定数kは全角率が1という条件から

  $$
  k=\frac{1}{B(p,q)}
  $$

• ベイズ統計学は、確率分布の母数を確率変数として扱う

• 母数（パラメータ）：確率分布を規定する定数

6章 ベイズ統計学入門

• 従来の統計学では、母数が主役で出発点

  • 確率分布の母数が定数
  • 規定された確率分布からデータの生起確率を算出し、母数の妥当性を確かめる

• ベイズ統計学では、データが主役で出発点

  • 確率分布の母数を確率変数
  • データからその母数の分布を調べる

• 母数をベイズの展開公式の原因Hと考える

  • データがDのときに母数の値がθiである確率を与える公式と考える

  $$
  P(\theta
  _1|D) =
  \frac{P(D|\theta
  _1) \cdot P(\theta
  _1)}
  {P(D|\theta
  _1)P(\theta
  _1)+P(D|\theta
  _2)P(\theta
  _2)+P(D|\theta
  _3)P(\theta
  _3)}
  $$

  • 事後確率：データDが得られた時、それが母数θの確率分布から得られた確率

  • 尤度：母数θの確率分布の下でデータDが得られる確率

  • 事前確率：データDを得る前の母数θの生起確率

  • 分母は、データDを得るときの確率。=P(D)

    $$
    k=\frac{1}{P(D)}
    $$

    $$
    P(\theta_1|D) =
    kP(D|\theta_1) \cdot P(\theta_1)
    $$

  • 母数が連続変数の場合

  離散変数	連続変数
  （事前確率）P(θi)	（事前分布）π(θ)
  （尤度）P(D	θi)
  （事後確率）P(θi	D)

  $$
  \pi(\theta|D)=kf(D|\theta)\pi(\theta)
  $$

  • 事後分布は尤度と事前分布の積に比例する

  • これをベイズ統計学の基本公式

  • 尤度は母数θが与えられた時のデータDの生起確率。確率分布における確率密度関数値

    • 事前分布に一様分布を仮定すると従来の統計学とベイズ統計学の結論は一致する
    • 一様分布の時比例定数は１とした。有名な確率分布においては公式が用意されている
    • 公式がない分布の場合にはMCMC法により導出できる

  • MAP推定：事後確率の分布の最大値で母数の値を推定する方法

    • ベイズ統計の結果は、経験や直感と一致する

  • データを1つにまとめて尤度を設定することもできる

    • ベルヌーイ分布に従うデータに対して、事前分布をベータ分布にとると、得られた事後分布は再びベータ分布に収まる

  • 自然な共役分布：ある分布に従うデータに対して、事前分布に特定の分布を指定すると、事後分布がその特定の分布と同じパターンに収まる

    • 自然な共役関係を利用することでその分布の公式が使える

    データの分布	事前分布	事後分布
    ベルヌーイ分布	ベータ分布	ベータ分布
    正規分布	正規分布	正規分布
    正規分布	逆ガンマ分布	逆ガンマ分布
    ポアソン分布	ガンマ分布	ガンマ分布

  • 規格化の条件：確率の総和が1になる

    • 離散：確率分布表の総計が１
    • 連続：確率密度関数のグラフとx軸とで囲まれた部分の面積が1になる

  • 最尤推定法：母数を含む尤度関数（尤度）の値が最大になるときに、確率p実現されると考えること。尤度関数が最大値を与えるように母数を決定する方法。そこで得られた母数の値を最尤推定値