概要
AI がバズワードと言われて数年が経ち、近年では当たり前のように AI を組み込んだアプリケーションがリリースされている。そんな中、自分も最低限は AI について理解しなければと思い、今更ながら学ぶことにした。目標は Tensorflow か Keras かを使って AI が組み込まれた何かしらのアプリケーションを作ること。(画像分類系が良さそう?まだ検討中)
自分はせいぜい、Kaggle でタイタニック号の死者を予測する AI (回帰問題?)を友人からハンズオンで教わりながら作った程度で、数学もほとんど分からないので知識はほぼゼロと言って良いと思う。ハンズオンで自分が学んだ内容は kernel7c32b41829 | Kaggle に軽くまとめてある
ただ、分類問題だとまた手順も変わってくるとは思うので、その辺も含めてゼロから学んでいこうと思う。似たような記事は多くあると思うが、本記事は自分のメモ代わりということもあり、学びがあり次第随時更新していく予定で進める。
もし AI 有識者の方がこの記事を見て間違いがありましたら、コメントにて訂正していただけますと幸いです。
教材について
基本的にはオライリーの「ゼロから作るDeepLearning」をベースに学びつつ、疑問に思ったことはググる形で進めていく。Tensorflow を使うならこの教材じゃなくても良いのでは?という話もあるかもしれないが、ニューラルネットワークのライブラリを使う上でその仕組が分からないと上手く扱える気がしなかったので読むことにした。
読んでみた印象としては、分類問題の話が大半で、回帰問題はまた別なのかな?と思った。学ぶにつれてこれも理解出来るようになるとは思う。
基礎的な用語
耳にしたことがある言葉をざっくりまとめた。
| 用語 | 意味 |
|---|---|
| 機械学習 | 特徴量を人間が定義 (とはいえ深層学習も機械学習の一種?) |
| ニューラルネットワーク (NN) | 特徴量を自動で定義することが可能 (学習) |
| ディープラーニング (深層学習) | NN の層を深くしたもの、精度が NN より高いが複雑 |
| 強化学習 | ニューラルネットワークとはまた別の手法のAI |
| Tensorflow | ニューラルネットワークのライブラリ |
| Keras | Tensorflow を使いやすくしたもの |
| Kaggle | AI 版の競技プログラミングみたいなもの |
| DNN | ディープニューラルネットワーク, ディープラーニングのこと? |
| CNN | 畳み込みニューラルネットワーク, 画像系で便利らしい |
| RNN | 再帰的ニューラルネットワーク, 時系列が関係するデータで使えるらしい |
| GAN | 敵対的生成ネットワーク, 入力データに似た何かを出力する |
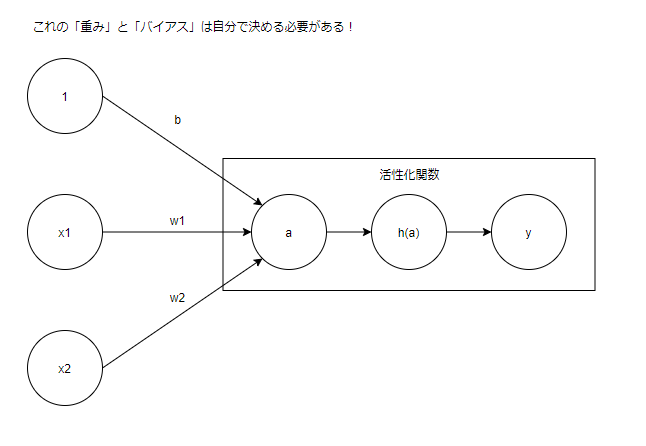
パーセプトロン
- ニューラルネットワークの元になっているアルゴリズム
- 入力に重みを掛けてバイアスを足した物を入力の総和として扱う
- 活性化関数: 入力の総和(a) を引数で受け取り、値に合わせて出力する
- パーセプトロンの活性化関数には「ステップ関数」が使われている
- パーセプトロンは組み合わせて層を作ることが可能 (多層パーセプトロン)
変数/関数/数式のメモ
今後も使うのでメモしておく。
| 項目 | 変数/関数 |
|---|---|
| 入力 | x |
| 重み | w |
| バイアス | b |
| 入力の総和 | a |
| 活性化関数 | h(a) |
| 出力 | y |
- 入力の総和: a = b + x1w1 + x2w2 ...
- ステップ関数の挙動: 0: a <= 0, 1: a > 0
- パーセプトロンの出力: y = h(a)
ニューラルネットワーク (NN) の基礎
- 多層パーセプトロンの活性化関数で「ReLU関数」「シグモイド関数」等を使ったもの
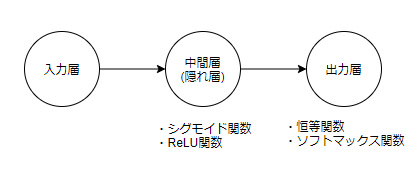
- 「入力層/中間層(隠れ層)/出力層」で構成されている
- パーセプトロンで自分で決めていた「重み」と「バイアス」をデータから自動で定義
各層についての説明
- 入力層: 複数の入力がある
- 中間層: 活性化関数 (シグモイド関数, ReLU関数) 、学ぶに連れて他にも色々出てくる
- 出力層: 恒等関数/ソフトマックス関数で出力、学ぶに連れて他にも色々出てくる
活性化関数について
| 関数名 | 役割 |
|---|---|
| ステップ関数 | 0 か 1 かしか出力しない |
| シグモイド関数 | ステップ関数をより滑らかにした形で出力する |
| ReLU関数 | 0 を超えていたらそのまま出力する |
出力層について
| 関数名 | 役割 |
|---|---|
| 恒等関数 | 入力をそのまま出力、回帰問題で利用される |
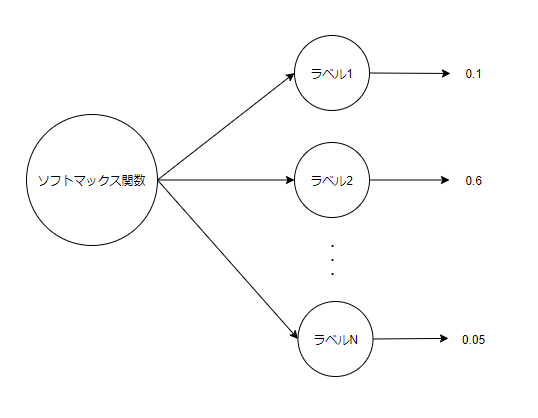
| ソフトマックス関数 | 入力の総和が1になるように出力、分類問題で利用される |
ソフトマックス関数は入力の総和が1になる。
つまり、それぞれの出力を確率として捉えてラベルごとに分類することができる。
(下記の図だと、ラベル1が10%, ラベル2が60%, ラベルNが5%となっている)
ニューラルネットワークの学習について
ここで言う学習はソフトマックス関数を使った「分類問題」に焦点を当てている。
- 学習とは適切な「重み」と「バイアス」をデータから自動で求めることである
- 学習には「訓練データ(教師データ)」と「テストデータ」を準備する
- 学習用データにはそれが何かを表す「ラベル」も準備する必要がある
- 学習用データが悪いとテストデータは汎化能力を正しく評価するために利用する
- 特定のデータセットにだけ対応した「過学習」と呼ばれる状態になることがある
学習の仕組みについて
- 学習を行う際の指標は「損失関数(コスト関数)」を利用、性能の悪さを出力する (数字が小さいほうが優秀)
- 損失関数には「2乗和誤差」と「交差エントロピー誤差」が使われる
- 損失関数で使うのは「ニューラルネットワークの出力 (y)」「教師データのラベル (t)」
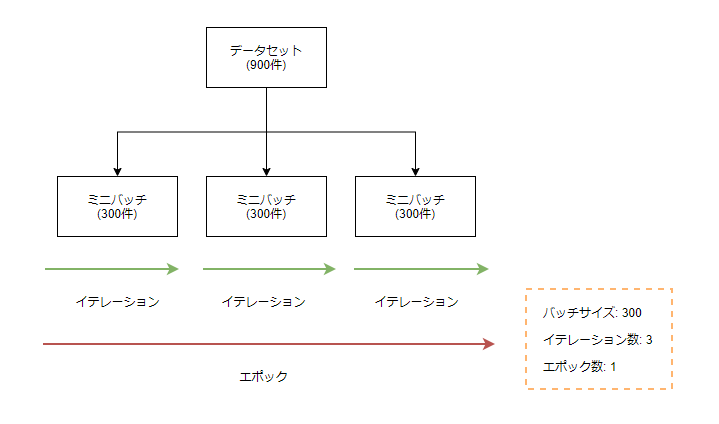
- 学習データが多すぎると時間がかかるので、一部のみを全体の近似として利用する: ミニバッチ学習
- 損失関数の値を小さくするために数値微分を行い、重みパラメータの「勾配」を求める
- 勾配は適切な重みパラメータを表し、勾配方向に重みパラメータを更新する事で精度を上げる
- 損失関数の出力がなるべく小さくなるように勾配を求めて重みを更新し続けることを「学習」という
学習の流れ (確率的勾配降下法: SGD)
- ミニバッチ: 訓練データからランダムに一部のデータを抽出
- 勾配の算出: 各重みパラメータの勾配を求める
- パラメータの更新: 重みを勾配方向に微小量だけ更新する
- 上記3つを繰り返す
- テストデータで学習したモデルの汎化能力を評価
誤差逆伝播法とは?
- 上記のように数値微分で勾配を求めるのはシンプルだが計算に時間が掛かる
- そこで、勾配の計算では複雑だが高速な「誤差逆伝播法」を用いる
- 逆伝播は「局所的な微分」を伝達、各変数の微分の値を効率よく求めることが可能
- ニューラルネットワークの各層を「レイヤ」で実装することで、勾配の計算を高速に求めることが可能
- この方式で勾配の計算を行うことを、誤差逆伝播法と呼ぶ
- レイヤには「順伝播 (forward)」と「逆伝播 (backward)」のインタフェースがある
- レイヤを組み合わせることで、自分の好きなニューラルネットワークを実装することが出来る
レイヤのメモ
今後出てくる物も少しだけまとめておく。
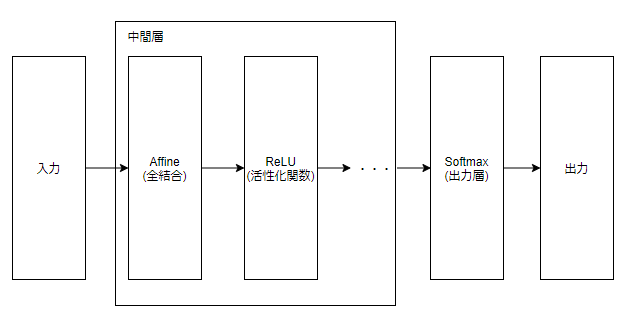
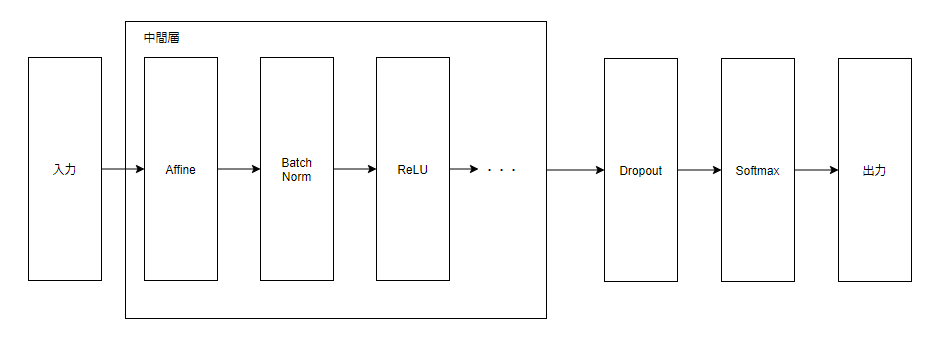
分類問題のニューラルネットワークにおける基本的な組み合わせは「入力 -> (Affine -> ReLU ...) -> Softmax」みたいな形で、これの精度を上げたり高速化したり堅牢にしたりするために他のレイヤを利用することもある。
| レイヤ名 | 役割 |
|---|---|
| ReULレイヤ | 活性化関数のReLU関数で実装されたレイヤ |
| Sigmoidレイヤ | 活性化関数のシグモイド関数で実装されたレイヤ |
| Affineレイヤ | 全結合層と呼ばれる、重み付き入力信号の総和を計算するレイヤ |
| Softmaxレイヤ | 出力層のSoftmax関数で実装されたレイヤ, 入力された値の総和が1になるように正規化する |
| CrossEntropyErrorレイヤ | 交差エントロピー誤差で実装されたレイヤ |
| Softmax-With-Lossレイヤ | softmaxレイヤ + CrossEntropyErrorレイヤ |
| Batch Normレイヤ | Batch Normalization で実装されたレイヤ, 学習高速化 |
| Dropoutレイヤ | Dropout で実装されたレイヤ, 出力層の手間に配置, 過学習を防ぐ |
| Convolutionレイヤ | 畳み込みを行うレイヤ, CNNで利用される |
| Poolingレイヤ | 縦/横方向を小さくするレイヤ, CNNで利用される |
学習に関するテクニック
- パラメータの更新方法は SGD だけではなく、「Momentum」「AdaGrad」「Adam」がある
- 重みの初期値は0だとダメで、ランダムな初期値が必要らしい <- 重みの初期値は大事
- 「Xavier の初期値」や「Heの初期値」を重みの初期値に使うといいらしい?
- 「Batch Normalizationレイヤ」を活性化関数の前に挟むと使うと学習を高速化出来る
- 過学習を防ぐための技術で「Weight decay」「Dropout」がある (これもレイヤとして実装する)
- Weight decay は複雑なニューラルネットワークには対応できず、Dropout を出力層の最初に挟むと良い
ハイパーパラメータ
重みやバイアスのように機械が決める物ではなく、人間が決めるパラメータ。
イテレーション数 * エポック数が学習の回数になる。
- バッチサイズ: 1つのミニバッチにあるデータ件数
- イテレーション数: 全データが1回以上学習に用いられるのに必要な学習回数 (全体データ数/バッチサイズ)
- エポック数: 同一イテレーションの学習回数、損失関数の値がほぼ収束するまで行う (完全に収束すると過学習になる)
その他のハイパーパラメータは下記の通り。(他にもありそう?)
- 各層のニューロンの数
- 学習係数
- 重みの初期値
畳み込みニューラルネットワーク (CNN)
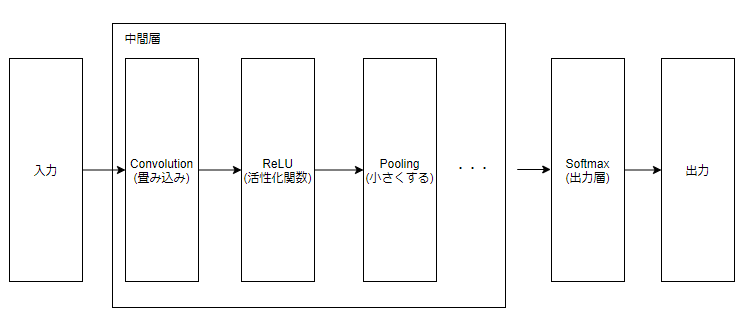
- CNN は画像認識や音声認識等、至るところで活用されている
- 「Convolutionレイヤ」と「Poolingレイヤ」が利用されるのが特徴的
- 「Affine - ReLU」になっていた部分が、「Conv -> ReLU -> Pooling」に置き換わる
- Affineレイヤはデータの形状が無視されてしまうのが問題 (1次元になる)
- Convolutionレイヤではデータ形状を維持することが可能 (画像の場合は縦/横/チャネル方向の3次元)
- CNNでは Conv レイヤの入出力データを特徴マップと呼ぶ
- ConvレイヤやPoolingレイヤの内容は難しくてよく分からなかった。
- 代表的なCNNの実装に「LeNet」と「AlexNet」がある
ディープラーニングとは?
- 層を深くしたディープなニューラルネットワーク
- 今までのニューラルネットワークを元に中間層を増やしたもの (同じ構造を隠れ層で2階層以上持つ)
- 実用例として「物体検出」「セグメンテーション」「キャプション生成」「画像生成」「自動運転」等がある
- Deep Q-Network: ディープラーニングを使った強化学習の手法もある
- 詳しいことはあまり良くわからなかったので、理解したら追記する
ここまでのまとめ
ディープラーニングの全体像
- 深層学習と言われているものは「ニューラルネットワーク」で実装されている
- ニューラルネットワークの学習は「適切な重みとバイアスを見つける」ことである
- 適切な重みとバイアスを見つけるには「損失関数」を指標にして、これを最小になるように目指す
- 損失関数の値を最小に近づけるには「勾配」を求める必要がある
- 勾配は数値微分で求められるが、より高速に求めるには「誤差逆伝播法」を使う
- 誤差逆伝播法では各層を「レイヤ」で実装し、レイヤを組み合わせることで自由に NN を実装可能
- 中間層のレイヤを増やしたものを「ディープラーニング」と呼ぶ
学習から分類までの流れ
- 教師データとテストデータを用意する (ラベルが必要)
- レイヤを組み合わせて NN を実装する (損失関数のレイヤを最後に組み込む)
- ハイパーパラメータを設定する
- 学習させる (損失関数の出力が最小になる重みとバイアスを誤差逆伝播法で得られる勾配から求める)
- 学習済みモデルにテストデータを分類させて汎化能力を評価 (過学習していないか)
最後に
難しくて分からないところも多々あったので、もう一度読み返したりググったりで更に理解を深めようと思う。また、今回は実際にコードを書いた訳では無いので、時間がある時に手を動かしてみるのも理解の助けになるかもしれないと思う。
次は「ゼロから作るDeepLearning2」を通じて RNN を使った自然言語処理について理解を深めようと思う。それと同時に Tensorflow か Keras を使って実際に何か分類系の AI を作ってみることを目指す。
最後になりますが、自分は AI についてド素人ですので、何か間違いがあればコメントにてご指摘いただけますと幸いです。