カルマンフィルターでパラメータ推定

天気予報では、モデル出力を予報変数（例えば、最高気温など）に変換するのに、カルマンフィルターを用いて、パラメータ推定を行っています。その手法については、気象庁（1997）に記載されています。

パラメータ推定

時間依存がない場合

ここでは、 $y = ax + b$ という線形の式の$a$と$b$を推定してみる。$y_i = a x_i + b + v_i $式を用いて、模擬データを生成し検討してみる。

$a = 2$、$b = 5$とし、$x$は-5から5の一様乱数とし、$v_i$は、平均0、標準偏差2のガウス乱数を与える。

KLM.py

def update(P, C, R, x_hat, obs, I):
  """
  P: 誤差共分散行列
  C: 観測系数行列
  R: 観測ノイズ分散行列
  """
  #カルマンゲイン
  G = P * C / (C.T * P * C + R)
  x_hat = x_hat + G * (obs - C.T * x_hat)
  P = (I -  G * C.T) * P
  return x_hat, P

a = 2.
b = 5.

x = np.random.uniform(-5, 5, 365)
v = np.random.normal(0, 2, 365)
y = []
for i in range(365):
    y.append(a * x[i] + b + v[i])
    
A = np.mat([1])
P = np.mat([[1, 0], [0, 1]])
R = np.mat([1])
I = np.identity(2)
x_hat = np.mat([[0], [0]])

for i in range(365):
  C = np.mat([[x[i]], [1]])
  obs = np.mat([y[i]])
  x_hat, P = update(P, C, R, x_hat, obs, I)

推定された$a$、$b$を図示すると、

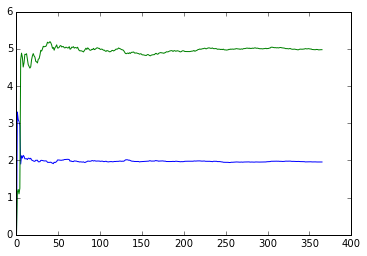
となり、短時間の間に、$a$、$b$が推定されているのが見える。

時間依存がある場合

途中でモデルが変わった場合やパラメータが季節変動している場合。
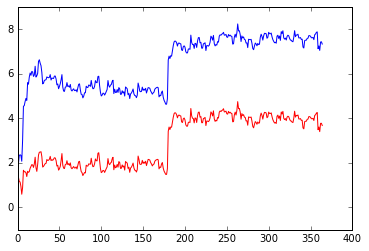
今回は180日目で係数にそれぞれ2が加わった場合。

KLM2.py

import numpy as np

def update(P, C, R, x_hat, obs, I):
  """
  P: 誤差共分散行列
  C: 観測系数行列
  R: 観測ノイズ分散行列
  """
  #カルマンゲイン
  G = P * C / (C.T * P * C + R)
  x_hat = x_hat + G * (obs - C.T * x_hat)
  P = (I -  G * C.T) * P
  return x_hat, P

a = 2.
b = 5.

x = np.random.uniform(-5, 5, 365)
v = np.random.normal(0, 2, 365)
y = []
for i in range(365):
    if i < 180:
        y.append(a * x[i] + b + v[i])
    else:
        y.append((a + 2) * x[i] + (b + 2) + v[i])

A = np.mat([1])
P = np.mat([[1, 0], [0, 1]])
R = np.mat([1])
S = 0.1
I = np.identity(2)
x_hat = np.mat([[0], [0]])

for i in range(365):
  C = np.mat([[x[i]], [1]])
  obs = np.mat([y[i]])
  P = P + S ** 2
  x_hat, P = update(P, C, R, x_hat, obs, I)

見事に変化に追従しました。

参考文献

気象庁（1997） 最新数値予報ガイド 第5章アプリケーションシステム 1カルマンフィルター　pp.66 - 78