はじめに
これは数学とコンピュータⅡ Advent Calendar 2017の12/17日の記事1となります。
自分はMSX・FANとベーマガ2育ちで、プログラムの習い初めで投稿者のソースコードを眺めていると「+1」や「-1」をしているところがありました。
たった 1 という自然数(0を含めない)の最小値ではありますが、これが無いとエラーになったり正常に動作しなくなるわけです。
数学面では 1 を最大値として扱うことでいろいろな応用ができます。
事例
プログラムを組めるようになるとその必要性が分かってきます、数学でも似たような事例がありますよね。今回は列挙してみます。
配列
ソースコードで「+1」や「-1」をしているのは、配列に関連していることが多いです。
配列の添字開始は0からが一般的となっているため、例えば配列の添字に合わせループにて順位(1~)を表示した際には+1します。
int[] array = new int[] {1,2,3};
int sum = 0;
for(int i=0; i<array.Length; i++){
sum += array[i];
Console.WriteLine(string.Format("{0} : {1}", i + 1, sum));
}
// 結果
1 : 1
2 : 3
3 : 6
R言語、MATLAB、COBOLの添字は1から始まります。VB6.0 では、Option Base ステートメントによって、配列の開始添字を 0 からではなく 1 に変更できました。VB .NET はサポートしていません。
余り(剰余)
余り(剰余)とは、除算によって「割り切れない」部分を表します。よって、商の値を絶対超えることはありません。0~商-1 の範囲の値を返します。
例えばカレンダーを作成する場合、剰余演算子「%」を使い「(日-1) % 7」とすることで0~6の値が返り、曜日の位置を揃えることが出来ます。
2017/12/01(金)~2017/12/15(金)
| 日-1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 余り | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 曜日 | 金 | 土 | 日 | 月 | 火 | 水 | 木 | 金 | 土 | 日 | 月 | 火 | 水 | 木 | 金 |
分離量(離散量)と連続量
仕事で固定長ファイルの192桁目~197桁目に値をセットする(不足は空白で埋める)というのがあり、target.PadRight(197-192)とやってしまったところ1桁分足りなかったです。正しくは、target.PadRight(197-192 + 1)とする必要がありました。
string target = "123";
// 結果 [123 ]
Console.WriteLine("[" + target.PadRight(197-192) + "]");
// 結果 [123 ]
Console.WriteLine("[" + target.PadRight(197-192 + 1) + "]");
| 桁 | 192 | 193 | 194 | 195 | 196 | 197 |
|---|---|---|---|---|---|---|
| 個数 | 1 | 2 | 3 | 4 | 5 | 6 |
個数や人数など0を含む整数で表現できるものは「分離量」であり、長さ、時間、重さ、面積などは「連続量」である。
今回は分離量であり、個数としては「+1」する必要がある。
| 連続量 | 分離量 |
|---|---|
| 2時~5時(3時間) | 2日~5日(4日間) |
| 2m~5m(3m) | 2本目~5本目(4本) |
補数表現
補数表現は一般的には2進数の「1の補数」と「2の補数」が有名ですが、実は全ての「n進数」に補数という概念が存在します。今回は説明として「2の補数」を扱います。
1の補数は2進数にした数値の1と0を逆転したもので、2の補数は1の補数に「+1」したものです。
そもそもコンピュータは0と1だけの世界なので、マイナスの数という概念はありません。そのため人間の目から見てマイナスの数を表すルールを決めます。通常は最上位桁を正負の判定にします。
8bitの2進数0000 0000~1111 1111は、補数表現でない場合は10進数の 0~255 となります。補数表現で最上位桁(8ビット目)が1であればマイナスの数を表した場合 -128~127 となります。
マイナスの方が128でプラスの127より1つ多いです、よって2の補数(マイナスの表現方法)では「+1」を行います。
パイプライン処理
基本情報で出題される。パイプラインは 1 つの命令についてその構成するステージを 1 つずつずらして実行し全体としての見かけの高速化を図る。
パイプライン処理の公式 $(I+D-1) \times P$
命令数(I)が4、深さ(D)が3、ピッチは1サイクルなので、(4+3-1)×1=6(サイクル)
等差数列の和
のちの天才数学者ガウスが小学生時代のある時、1 から 100 までの数字すべてを足すように課題を出された。それを彼は、1 + 100 = 101, 2 + 99 = 101, …, 50 + 51 = 101 となるので答えは 101 × 50 = 5050 だ、と即座に解答して教師を驚かせたという逸話があります。
${\displaystyle S=\frac{(n+1)n}{2}} = (100 + 1) \times 100 \div 2 = 101 \times 50 = 5050$
線形探索法の平均比較回数
線形探索法の平均比較回数は、${\displaystyle \frac{(n+1)}{2}}$ です。
データ数 $n$ が $1$ のとき、比較回数を $1$ にするため。
平均は総和を数で割ったものなので 等差数列の和の公式 n(n+1)/2 を n で割れば
(n+1)/2 になります。
線形探索法の平均比較回数は(n+1)/2ですが、なぜ+1しているのですか?
※情報処理試験などではデータが大きい場合等の前提条件をつけて、$+1$ していない回答があります。
円順列・数珠順列
円順列
異なるn個のものを円形に並べる順列です。
円卓に自分1人が先に座って固定 $(-1)$ し、残った $(n-1)$ 人を後から座らせる。
${\displaystyle n! \div n = (n-1)!}$
例 5人が円卓に座る方法は何通りあるか
$(5-1)!=4!=4 \times 3 \times 2 \times 1 = 24$
数珠(じゅず)順列
「円順列」で時計回り、反時計に読んで一致するものを同じとみなす順列となります。重複分として 2 で割ります。
${\displaystyle \frac{(n-1)!}{2}}$
確率
確率を表す場合、論理的にはパーセントの値はかならず100以下となります。しかし、絶対合格するというふうに「絶対」を強調する目的で、俗に「120%の確率で合格する」とか「合格する可能性は200%だ」というふうに比喩的に表現することがあります。
間違えないで欲しいのは「割合」なら、1.2倍を120%と表現します。
確率の身近な例で考えると、天気の降水確率があります。降水確率10%ということは傘は不要だと判断しますよね。
晴れの確率とは雨の降らない確率となるので、全体(100%)から降水確率10%を引いた90%となります。計算する上では100%は使わず「1」を使います。
$1 - 降水確率(0.1) = 晴れの確率(0.9)$
$降水確率(0.1) + 晴れの確率(0.9) = 1$
オッズ
オッズ(odds)は、確率論で確率を示す数値。ギャンブルなどで見込みを示す方法として古くから使われています。
オッズ ${\displaystyle Odds}$と確率 ${\displaystyle p}$ には以下の関係式が成り立つ。
${\displaystyle Odds={\frac {p}{1-p}}}$
${\displaystyle p={\frac {Odds}{1+Odds}}}$
オッズは競馬などギャンブルのブックメーカーが見込みを示す方法として使われており、5回に1回の確率(つまり0.2または20%)で起きる事象は、オッズで表すと次のようになる。このオッズが低いほど、その事象が起きた場合の儲けが多くなる。
${\displaystyle Odds={\frac {0.2}{1-0.2}} = \frac {0.2}{0.8} = 0.25}$
ロジスティクス回帰分析
ここ数年は機械学習がブームですね、ロジスティクス回帰分析では単・重回帰分析と違って確率をつかいます。
ロジスティクス回帰分析で使われる標準シグモイド関数
${\displaystyle log_e{\frac {p}{1-p}}}=\beta_0 + \beta_1x_1 + \beta_2x_2 \cdots + \beta_{k}x_{k}$
式を変形します。
$t=\beta_0 + \beta_1x_1 + \beta_2x_2 \cdots + \beta_{k}x_{k}$ とおく
${\displaystyle exp \Bigl(log_e{\frac {p}{1-p}}}\Bigr)=exp(t)$
${\displaystyle \frac {p}{1-p}=exp(t)}$
両辺に$1-p$ を掛けて
${\displaystyle \frac {p(1-p)}{1-p}=exp(t)(1-p)}$
分母を払い簡略化して
$p=exp(t)-p \times exp(t)$
$-p \times exp(t)$ を移項して
$p \times exp(t)+p=exp(t)$
$p$ でまとめて
$(1+exp(t))p=exp(t)$
$1+exp(t)$ で両辺を割って、最終的に次のようになります。
${\displaystyle p=\frac {exp(t)}{1+exp(t)} \Bigl(=\frac{1}{1+exp(-t)}\Bigr)} $
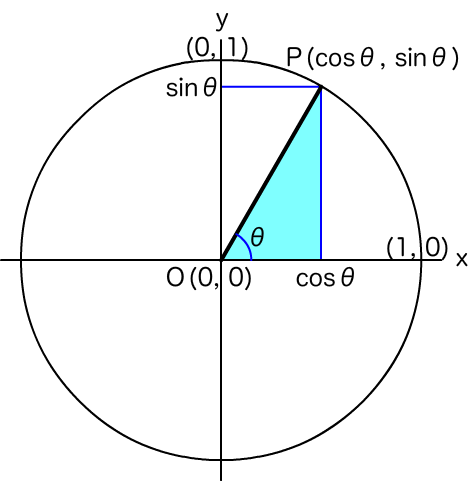
三角関数
三平方の定理から以下の公式が導き出される(三角比の相互関係)
${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1}$
${\displaystyle 1+\tan ^{2}\theta ={\frac {1}{\cos ^{2}\theta }}}$
三角関数は半径 1 の円周上のxy座標が角度θに対して(cosθ, sinθ)と定められている。よって最大値が 1、最小値 -1 となる。
正規化
正規化座標
正規化座標は、0 から 1 までの値をとる(u,v)座標を指す。
最小値 0と最大値 1による正規化では、データを特定の範囲、たとえば 0 ~ 1の間に線形変換します。
ポリゴンに絵を貼るテクスチャマッピングは(u,v)座標を使用しています。
3Dを基礎から勉強する テクスチャマッピング
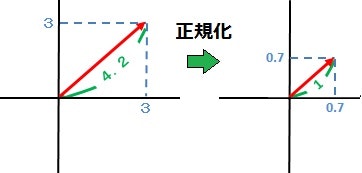
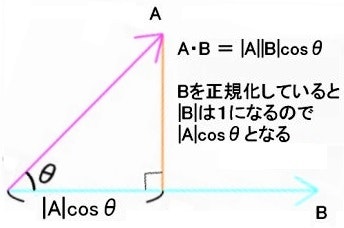
ベクトルの正規化
ベクトルの正規化とは、ベクトルの方向は維持しつつ大きさを「1」にする事を指します。この大きさが「1」のベクトルのことを単位ベクトルと呼びます。
3Dを基礎から勉強する 正規化
単位ベクトルを作っておけば、定数倍して簡単にいろんな大きさのベクトルが作れるようになります。
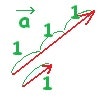
三角関数は半径 1 なので、正規化することで簡略化できるようになります。
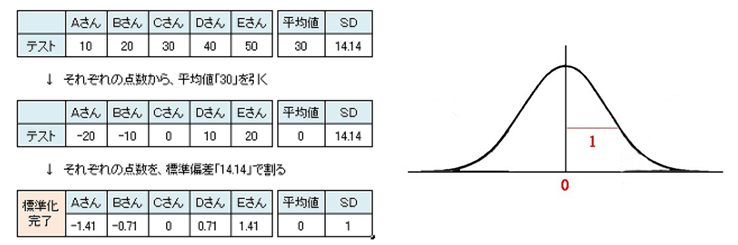
データの標準化
例えば、ネジの長さのデータを分析し比較する際、ミリとインチのように単位がばらばらだと比較ができません。
標準化することで、単位の違いを無視することができます。
その方法は平均値が0、標準偏差が1になるように正規化する。
虚数・階乗・指数
| 項目 | 式 |
|---|---|
| 虚数 | $i^2 = -1$ |
| 階乗 | $0! = 1$ |
| 指数 | $a^0 = 1$ |
虚数
虚数単位 i とは、2次方程式 x2 + 1 = 0 の2つの解のうちの一方のこと。
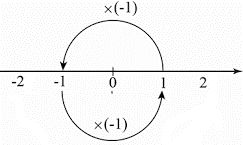
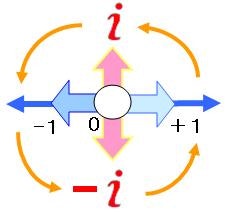
後述する複素数平面上では90度を虚数 i とし、それを180度回転すると、虚数 -i となります。
階乗
ゼロの階乗を「0」ではなくて「1」と定義するという考え方です。
「1の階乗」は、「0の階乗」に「1」を掛けたものになりますので、「0の階乗」だけは「1」でスタートしておかないとおかしいというわけです。
$2! = 2! \times 1!$
$1! = 1! \times 0!$
$0! = 1! \div 1 = 1$
指数
ある数をx乗するとは、ある数をx回かけ算するということです。
$2^3 = 2 \times 2 \times 2 = 8$
$2^2 = 2 \times 2 = 4$
$2^1 = 2$
2の3乗⇒2乗⇒1乗と指数が1ずつ少なくなるにつれて、答えが ${\displaystyle \frac{1}{2}}$になっていきます。つまり、$2^0 = 2 \div 2 = 1$ になります。
この方法だと指数がマイナスになっていってもどういう数字になるのか予想出来ますよね。
複素数
オイラーの公式に $x=π$ を代入すると
$e^{{i\theta }}=\cos \theta +i\sin \theta$
$e^{{i\pi }}=-1 + i x 0$
$e^{{i\pi }}=-1$
$eiπ + 1 = 0$
「マイナス✕マイナスは、なぜプラスか」は、180度回転すると考える、90度は虚数 i を使います(複素数平面)。
最後に
いかがだったでしょうか。まだ他にもたくさん事例があると思います。
自然数の最小値 1 ですが、確率や正規化や三角関数のように 1 を最大化として扱うことで、他の数式にも応用出来たりするわけです。
-
予定では射影変換で4年前の自記事「射影変換(ホモグラフィ)について理解してみる」の整理でした。 ↩
-
PC-8801のプログラムが2本採用されました。 ↩