はじめに
私はほとんどゲームをやらないので、「ドラゴンクエスト」や「ファイナルファンタジー」などナンバリングタイトルが多いタイトルを見ると思い入れが無いだけに、ⅣとⅥとⅨとⅪが幾つなのか混同してしまう。
2017/02/18(土)に開催した「Shizuoka.py #6 and shizudev」用に「数学史 黎明期」のセッション資料を作成した際に、ルールが分かり混同しなくなったので知識を共有する。
ルール
ローマ数字では4つ以上同じ記号を並べないようになっています。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII |
I が 1 で、これを 2 本重ねて II とすれば 2 で、3 本重ねて III とすれば 3 を意味します。V は 5 を意味します。
左側に I をつけると「 1 つ少ない」(マイナス)を意味するので、4 は IV と表記します。右側につけると「プラス」を意味し、VI は 6 を意味します。X は 10 です。
ある本に書かれていたのですが、ローマ数字は足し算(引き算)を内包しているという言葉がしっくりきました。確かに II(2) = I + I、IV(4) = V - I 、VII(7) = V + I + I ですよね。
※時計の文字盤では IIII やVIIIIという表記を見かけることもあります。
参照:ローマ数字と時計数字
ローマ数字の由来
ローマ数字の由来の説が面白い。
— 横山 明日希 (@asunokibou) March 1, 2023
羊の数を数える時、木に刻んでいた。数えやすくするために5区切りで刻み方を変えていた(5は「Ⅴ」で10は「Ⅹ」)。
なので4は「Ⅴ」に加えて手前の刻んだ跡を含めた「Ⅳ」となった。 pic.twitter.com/5QfCc6LnwS
桁記号記数法
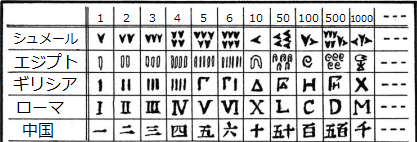
現在、私達が日常的に使用しているのはアラビア数字であり、位が変わっても同じ数字(1,2,3,4,5,6,7,8,9,0という10個の数字)を使用する「位取り記数法」を使っていますが、古代ではある大きさの値になると別の記号を使う「桁記号記数法」を使っていました。
使用例
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
|---|---|---|---|---|---|---|
| I | V | X | L | C | D | M |
13 = 10 x 1 + 1 x 3
= X + III
= XIII
24 = 10 x 2 + (−1 + 5)
= XX + IV
= XXIV
3888 = 1000 x 3 + 500 + 100 x 3 + 50 + 10 x 3 + 5 + 1 x 3
= MMM + D + CCC + L + XXX + V + III
= MMMDCCCLXXXVIII
ローマ数字では4つ以上記号を並べないというルールがあるので、他の記号でも4つ以上並ぶようなら、(−1 + 次の位の記号)のようにします。
49 = (-10 + 50) + (−1 + 10)
= XL + IX
= XLIX
計算器具
足し算で先程の 13 + 24 = 37をローマ数字で数を表してみます。
XIII
+ XXIV
-------
XXXVII
このように桁記号記数法では計算が大変なため、「アバカス」という計算器具が使われていました。これは後にシルクロード経由で中国に伝わり17世紀に中国の明から日本に伝わって、現在の「そろばん」となりました。
アラビア数字
現在、一般に使われているのはアラビア数字(ほんとはインド数字)です。
アラビア数字は位が変わっても1,2,3,4,5,6,7,8,9,0という10個の数字だけで済み、位により新しい記号を作る必要がありません。
記数法のかんたんな歴史 ― アレッサンドラ・キング - TED Ed
アル・フワリズム(Al Khawarizmi)が825年に著した算術書「インドの数の計算法」(ラテン語訳の題名は, ”Algorithmi de Numbers Indorum”)があります。
インド数字はこの算法とともに13世紀以降にイタリア(レオナルド・フィボナッチが1202年に出版した「算盤の書」でインドの方法を紹介)からヨーロッパに広がりアラビア算用数字と呼ばれるようになりました。
「アルゴリズム」の語源は、このアル・フワリズムという人の名前となります。アラビア語からラテン語に翻訳した際に、名前と気が付かなかったとのこと。
未知数といえば「x」ですが、アラビア起源説というのがあります。
ゼロの発明
インドでは、ゼロの発明したとよく聞くが何のことかあやふやな知識のままでした。
ゼロには3つの使い方があります。
- 記号(空位)としてのゼロ
- 数(演算の対象)としてのゼロ
- 原点としてのゼロ
記号(空位)としてのゼロ
ただ何もないということの記号なら、古代バビロニア時代(60進法)にもありました。
例えば、アラビア数字のゼロ「0」を位の位置を表わした場合、一番右の数字は1の位、右から2番目の数字は10の位、右から3番目の数字は100の位といったルールになっています。
例で「307」は、1の位が7、10の位が空位、100の位が3であることを表してします。
古代インドでもゼロは空白で表していましたが、下記のようにすると見た目の表現的にも位の位置の区別が難しかったので、「0」を記号として使うようになった。
2 3 … (203)
2 3 … (2003)
数(演算の対象)としてのゼロ
古代エジプト辺りでは「図形の数学」として、「数」と「形」がセットで発達してきました。図形的に「0」は長さも面積もなく図形の世界には登場しないことから、意味をもたないと宗教的にも嫌われていましたが、インドでは「図形の数学」もそれほど発展せず、「数」が「形」に縛られる必要はなかった結果、インドのほうが数としての「0」の使用が進み、ヨーロッパはそれを取り入れる形になりました。
参照:ゼロってナニ!? ゼロを拒んだ古代の偉人たち
原点としてのゼロ
インドでは負債をあらわすときに負の数を使用していました。
ヨーロッパへはゼロの概念とともにアラビア経由で伝えられたが、ゼロの演算と同じく受け入れられるには時間がかかりました。ヨーロッパでは17世紀までマイナスの概念がなく「7-9」という引き算にすら答えを出すことが出来なかったのです。
負の数を初めて本格的に導入したのはデカルト座標で有名な「ルネ・デカルト」です。
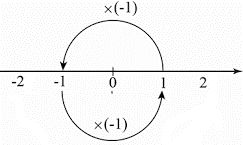
負の数は-3個のリンゴのように「個数」ではイメージしにくいですが、負の数を「数値線」に表すことでイメージしやすくなった。
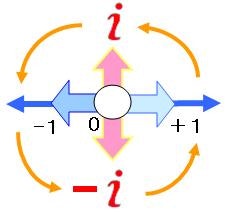
「マイナス✕マイナスは、なぜプラスか」は、180度回転すると考える、90度は虚数 i を使います(複素数平面)。
最後に
ローマ数字のことから、勢い余ってゼロの概念まで書いてしまいました。
歴史を知ると忘れにくくなると思うので、混同されなくなるんではないでしょうか。
あと、アラビア数字により位表記が簡単になった分、この前あった不二家のケーキ240個発注が誤発注で10倍の2400個も届いてしまうという負の面も起こり得てしまうので気をつけましょう。