はじめに
三角関数のサイン・コサイン・タンジェントはもちろん色んな使い方があるわけですが、有名なのは点を回転移動させることが出来ることです。
例えばアナログ時計をプログラムで作成しようとした場合、針の動きを実現するには三角関数を使用することになります。
Excelなどのアプリケーションでは画像を回転させることができます。画像といっても所詮は多くの点の集まりに過ぎません。
これは別ブログのリライト記事になります。
【2023/10/21追記】
Qiitaの数式ライブラリーの変更により、\\で改行が出来なくなっていました。
バージョンアップされるまでは、displaylinesで囲むようにしました。
画像の回転処理
画像の回転処理について、昨今ではAPI(例 CanvasのRotateメソッド)を使えば角度を指定するだけで画像が回転して表示されるので、裏の仕組みを知らなくてもいいわけです。
今回は、画像をCanvasのRotateメソッドを使用しないで自前で回転させてみます。
使用する画像は下記の猫にゃんです。

画像の回転は、画像を構成する全ピクセルの回転後の座標を計算して点を打つだけです。
回転をする場合の入力点(x1,y1)を、画像の中心(cx,cy)を回転の中心としてA度回転させる場合の出力点の座標(x2,y2)は下記の式となります。
\displaylines {
x2=(x1-cx) \times cos(-A) - (y1-cy) \times sin(-A) + cx\\
y2=(x1-cx) \times sin(-A) + (y1-cy) \times cos(-A) + cy
}
穴が空く
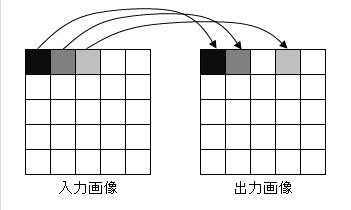
しかし、この計算式を使って実際に画像を回転させてみると、下記の画像のように穴が空いてしまいます。

これはコンピューター画像は1ピクセルが最小単位となっており、小数点がある座標(0.5,0.5)等を指定した場合には、どちらかに寄せる必要があります。例えば四捨五入した場合では、X方向なら右へ、Y方向なら下に寄ることになります。
//回転描画(穴が空く方式)
function drawRotate_Hole(degrees, offset){
var ctx = cvs.ctx;
var rad = -degrees / 180 * Math.PI;
var ct = new Point(texture.width / 2 , texture.height / 2);
var dstWidth = (Math.abs(texture.width * Math.cos(rad)) + Math.abs(texture.height * Math.sin(rad))) | 0;
var dstHeight = (Math.abs(texture.width * Math.sin(rad)) + Math.abs(texture.height * Math.cos(rad))) | 0;
var pixelImage = ctx.createImageData(dstWidth, dstHeight);
data = ctx.getImageData(0, 0, texture.width, texture.height).data;
var sx = (dstWidth / 2) | 0;
var sy = (dstHeight / 2) | 0;
ctx.fillStyle = "black";
for(var y=0; y<texture.height; y++){
for(var x=0; x<texture.width; x++){
var n = (y * texture.width + x) * 4;
var pt = rotate2d(x - ct.x, y - ct.y, rad);
var R = data[n + 0];
var G = data[n + 1];
var B = data[n + 2];
var A = data[n + 3];
var ptr = ((pt.y + sy) * dstWidth + (pt.x + sx)) * 4;
pixelImage.data[ptr + 0] = R;
pixelImage.data[ptr + 1] = G;
pixelImage.data[ptr + 2] = B;
pixelImage.data[ptr + 3] = A;
}
}
ctx.putImageData(pixelImage, offset.x, offset.y);
ctx.strokeRect(offset.x, offset.y, dstWidth, dstHeight);
}
※ちなみにHTML5のCanvasでは整数以外の座標でレンダリングすると、線が滑らかになるよう自動的にアンチエイリアスが使用されます。実は回転時の点を打つ際に最初はRectangleメソッドを使って実装していたのですが、穴があきませんでした。穴はアンチエイリアスの機能によって勝手に埋まってしまっていたのです。その為、createImageDataメソッドによる方法に変更しました。
穴が空かない
では、画像を回転させた場合に穴が空かないようにするにはどうしたらいいでしょう?

実は単純な逆転の発想です、入力座標から出力座標で計算させると整数にする際に誤差によって穴が空くわけですから、反対に出力座標から入力座標に逆計算させてあげればいいのです。
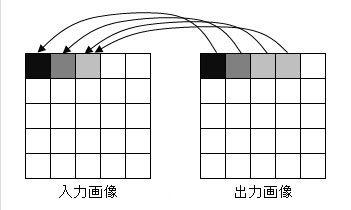
このときに用いる計算式は下記になります。逆計算のため、Aは-AからAと符号が変わっています。
\displaylines {
x1 = (x2-cx) \times cos(A) - (y2-cy) \times sin(A) + cx\\
y1 = (x2-cx) \times sin(A) + (y2-cy) \times cos(A) + cy
}
//回転描画(穴が空かない方式)
function drawRotate_NoHole(degrees, offset){
var ctx = cvs.ctx;
var rad = degrees / 180 * Math.PI;
var ct = new Point(texture.width / 2 , texture.height / 2);
var dstWidth = (Math.abs(texture.width * Math.cos(rad)) + Math.abs(texture.height * Math.sin(rad))) | 0;
var dstHeight = (Math.abs(texture.width * Math.sin(rad)) + Math.abs(texture.height * Math.cos(rad))) | 0;
var pixelImage = ctx.createImageData(dstWidth, dstHeight);
data = ctx.getImageData(0, 0, texture.width, texture.height).data;
var sx = (dstWidth / 2) | 0;
var sy = (dstHeight / 2) | 0;
ctx.fillStyle = "black";
for(var y=0; y<dstHeight; y++){
for(var x=0; x<dstWidth; x++){
var pt = rotate2d(x - sx, y - sy, rad);
if((pt.x + ct.x) < 0 || (pt.y + ct.y) < 0 ||
(pt.x + ct.x) > texture.width || (pt.y + ct.y) > texture.height) continue;
var n = ((pt.y + ct.y) * texture.width + (pt.x + ct.x)) * 4;
var R = data[n + 0];
var G = data[n + 1];
var B = data[n + 2];
var A = data[n + 3];
var ptr = (y * dstWidth + x) * 4;
pixelImage.data[ptr + 0] = R;
pixelImage.data[ptr + 1] = G;
pixelImage.data[ptr + 2] = B;
pixelImage.data[ptr + 3] = A;
}
}
ctx.putImageData(pixelImage, offset.x, offset.y);
ctx.strokeRect(offset.x, offset.y, dstWidth, dstHeight);
}
画像の自前回転処理
http://jsdo.it/yaju3D/iPx2

回転行列
上記では行列を使用していませんでした。
この際、勢いに乗って三角関数のついでに回転行列まで説明してしまいましょう。
先程、回転をする場合の入力点 $(x1,y1)$ を、画像の中心 $(cx,cy)$ を回転の中心として $A$ 度回転させる場合の出力点の座標 $(x2,y2)$ は下記の式を使いました。
\displaylines {
x2 = (x1-cx) \times cos(-A) - (y1-cy) \times sin(-A) + cx\\
y2 = (x1-cx) \times sin(-A) + (y1-cy) \times cos(-A) + cy
}
説明を単純化する上で、画像の中心 $(cx,cy)$ は原点 $(0,0)$ として省略、A度は $\theta$ にします。
\displaylines {
x2 = x1 \times \cos\theta - y1 \times \sin\theta\\
y2 = x1 \times \sin\theta + y1 \times \cos\theta
}
$(x2,y2)$ は $(r.x,r.y)$、$(x1,y1)$ は $(p.x,p.y)$ に変更して順番を入れ替えます。
よって、回転で使用する式を以下とします。
\displaylines {
r.x = \cos\theta \times p.x - \sin\theta \times p.y\\
r.y = \sin\theta \times p.x + \cos\theta \times p.y
}
数学的に式を単純化してみると、$(r.x,r.y)$ を分けているのを $r$ のみ、$(p.x,p.y)$を分けているのを $p$ のみ、$sin$ と $cos$が入った何かを $A$ と置き換えます。
r = Ap
$A$ と $p$ をどうにかすると、$r$ となるという式に単純化されました。
$A$ を行列(Matrix)で表現してみます。
A=\begin{pmatrix}
cos & -sin \\
sin & cos
\end{pmatrix}
$A$ を横に2個、縦に2個の計4個の数字を並べてあり、横に並べたのを行といい、縦に並べたのを列といいます。
\displaylines {
r.x = \cos\theta \times p.x - \sin\theta \times p.y\\
r.y = \sin\theta \times p.x + \cos\theta \times p.y
}
上記式を行列で再表現してみると以下のようになります。
\begin{pmatrix}
r.x \\
r.y
\end{pmatrix}=
\begin{pmatrix}
cos & -sin \\
sin & cos
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y
\end{pmatrix}
行列計算のおさらいとして実際に数値を入れて計算をしてみると
\displaylines {
\begin{pmatrix}
x \\
y
\end{pmatrix}=
\begin{pmatrix}
1 & 2 \\
3 & 4
\end{pmatrix}
\begin{pmatrix}
5 \\
6
\end{pmatrix}
\\
\\
1 \times 5 + 2 \times 6 = 5 + 12 = 17\\
3 \times 5 + 4 \times 6 = 15 + 24 = 39\\
(x,y) = (17,39) となります。
}
回転だけでなく、拡大縮小と平行移動も考えてみます。
拡大縮小
拡大縮小は単純に点 $(x,y)$に倍率を掛けてあげればよい。
点 $(x, y)$を原点に関して $x$ 軸方向に $sx$ 倍、$Y$ 軸方向に $sy$ 倍する行列は以下となります。
\begin{pmatrix}
r.x \\
r.y
\end{pmatrix}=
\begin{pmatrix}
sx & 0 \\
0 & sy
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y
\end{pmatrix}
実際に数値を入れて計算をしてみます。点 $P(3,4)$ を $2$ 倍にする。
\displaylines {
\begin{pmatrix}
x \\
y
\end{pmatrix}=
\begin{pmatrix}
2 & 0 \\
0 & 2
\end{pmatrix}
\begin{pmatrix}
3 \\
4
\end{pmatrix}
\\
\\
2 \times 3 + 0 \times 4 = 6 + 0 = 6\\
0 \times 3 + 2 \times 4 = 0 + 8 = 8\\
(x,y) = (6,8) となります。
}
平行移動
次は平行移動です。
平行移動は素直に座標に対して、加算すればいいですね。
点 $P(1,2)$ に $x$ 方向に $3$、$y$ 方向に $1$ を加えた点 $R$ の位置は
\displaylines {
r.x = 1 + 3\\
r.y = 2 + 1
}
となり、点$R(4,3)$となります。
加算する値を $q$ で表した場合の式は以下になります。
\displaylines {
r.x = p.x + q.x\\
r.y = p.y + q.y
}
行列で表現した場合には、今までと違って行列の掛け算ではなく行列の足し算となります。
\begin{pmatrix}
r.x \\
r.y
\end{pmatrix}=
\begin{pmatrix}
px \\
py
\end{pmatrix}+
\begin{pmatrix}
q.x \\
q.y
\end{pmatrix}
回転と拡大縮小と平行移動をまとめて操作したい場合、回転と拡大縮小は行列の掛け算で平行移動だけが行列の足し算になると扱いにくいので平行移動も行列の掛け算で表現できるようにします。
行列の掛け算といっても、計算する列が変わると加算してましたよね。
つまり、列を増やしてあげれば加算できることになります。
\displaylines {
\begin{pmatrix}
r.x \\
r.y \\
1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & t.x\\
0 & 1 & t.y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y \\
1
\end{pmatrix}\\
r.x = 1 \times p.x + 0 \times p.y + t.x \times 1\\
r.y = 0 \times p.x + 1 \times p.y + t.y \times 1\\
r.x = p.x + t.x\\
r.y = p.y + t.y\\
}
最後の $1$ は、行列の乗算では掛けられる行列の列数($3$)と掛ける行列の行数($3$)が同じである必要があるため、ダミーとなります。
回転と拡大縮小と平行移動を全部行列の掛け算で表せることが出来ました。
では、並べてみます。
\displaylines {
回転行列\\
\begin{pmatrix}
r.x \\
r.y
\end{pmatrix}=
\begin{pmatrix}
cos & -sin \\
sin & cos
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y
\end{pmatrix}\\
拡大縮小行列\\
\begin{pmatrix}
r.x \\
r.y
\end{pmatrix}=
\begin{pmatrix}
sx & 0 \\
0 & sy
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y
\end{pmatrix}\\
平行移動行列\\
\begin{pmatrix}
r.x \\
r.y \\
1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & t.x\\
0 & 1 & t.y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y \\
1
\end{pmatrix}
}
平行移動だけが $3\times3$ 行列となっていますので、回転と拡大縮小も平行移動の行列数に合わせた式が以下になります。
\displaylines {
回転行列\\
\begin{pmatrix}
r.x \\
r.y \\
1
\end{pmatrix}=
\begin{pmatrix}
cos & -sin & 0\\
sin & cos & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y \\
1
\end{pmatrix}\\
拡大縮小行列\\
\begin{pmatrix}
r.x \\
r.y \\
1
\end{pmatrix}=
\begin{pmatrix}
sx & 0 & 0 \\
0 & sy & 0 \\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y \\
1
\end{pmatrix}\\
平行移動行列\\
\begin{pmatrix}
r.x \\
r.y \\
1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & t.x\\
0 & 1 & t.y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
p.x \\
p.y \\
1
\end{pmatrix}
}
このように2次元のアフィン変換をするには、$3\times3$ 行列を使います。
同じ理屈で3次元の場合は、$4\times4$ 行列が使われます。
逆行列を使用した座標変換
行列を説明したところで、逆行列を説明をしてみます。
行列には、足し算・引き算・掛け算は定義されているのですが、割り算は定義されていません。
では、行列で割り算が出来ないかというとそうではありません。
行列ではなく自然数の場合、$1$ に $3$ を掛けると $3$ となります。これを元の $1$ に戻す場合、「$3$で割る」ことで元の $1$ になりますが、「$1/3$を掛ける」としても元の $1$ になります。
この場合、「$3$で割る」とは言わずに「$1/3$を掛ける」と考えます。
割り算のかわりに逆数を掛けることで、割り算と同様の結果が求めることが出来るのです。
行列でも同じ様に「逆数を掛ける」に近い考え方をします。
行列に逆数を掛ける際に使用するのが、「逆行列」となるのです。
画像を回転させた時に穴が空くのは、転送元から転送先にピクセルを移動した際に、(0.5,0.5)など小数の座標があった場合に小さい方に寄せたりすると起きる問題でしたね。

これを解決するには、転送先から転送元にピクセルを移動すれば出来るということでしたね。
この時に逆行列を使用します。

転送元(src)から転送先(dst)に座標を求める変換行列を $T$ とすると
\begin{pmatrix}
x' \\
y'\end{pmatrix}=\Large T\begin{pmatrix}
x \\
y\end{pmatrix}
変換行列 $T$ を回転行列とすると
\begin{pmatrix}
x' \\
y'\end{pmatrix}=\begin{pmatrix}
cos & {-sin}\\
sin & cos\end{pmatrix}\begin{pmatrix}
x \\
y\end{pmatrix}
これを転送先(dst)から転送元(src)の座標を求めるのに使用するのが逆行列です。
\begin{pmatrix}
x \\
y\end{pmatrix}=\Large T^{-1}\begin{pmatrix}
x' \\
y'\end{pmatrix}
\Large T^{-1}=\frac{1}{cos^2+sin^2}\begin{pmatrix}
cos & sin \\
{-sin} & cos\end{pmatrix}
分母の $cos^2+sin^2$ は、ピタゴラスの定理で $1$ となるので消せます。
\Large T^{-1}=\begin{pmatrix}
cos & sin \\
{-sin} & cos\end{pmatrix}
これは回転角が $-\theta $ となった逆回転となります。参照:回転行列 - wikipedia
\begin{pmatrix}
x' \\
y'\end{pmatrix}=\begin{pmatrix}
cos & sin\\
{-sin} & cos\end{pmatrix}\begin{pmatrix}
x \\
y\end{pmatrix}
※今回説明上は $2 \times 2$ 行列にしましたが、一般的には平行移動も加えた $3 \times 3$ 行列が使われます。
最後に
私もIT業界に入って25年くらい経ちますが、業務で三角関数や行列を使用したことがありません。IT業界に長くいてもこんな状態です、一般な人が三角関数を使用しないのは理解します。今はライブラリーやAPIがそういった知識の部分を補ってくれるのですから、プログラマーとして知識欲がなければ知らないまま過ぎてしまうでしょう。
私の場合はゲームに興味があり、どういう原理が知りたいという思いがあったので記事を書けるくらいの知識は得ました。
三角関数を使用しないことと概念として知らないことは違うので、概念くらいは知っておくべきでしょうね。
今やゲームも3Dバリバリでとても美しく表示も速いです、あれば多くのポリゴンにテクスチャが貼られて光源が付いてリアルに表示されているわけです。こういうのもプログラマーとして仕組みを知りたいと思うかどうかですね。