はじめに
機械学習を学ぶようになり数学や統計の本やサイトに出てくる数式をみると2乗をよく見かけます。同じ数を2回掛けるってだけなのになんでなんだろう。
ネットで調べると「世界は2乗でできている 自然にひそむ平方数の不思議、小島寛之著」というピッタシの本がありました。Web上には書籍レビューや著者の小島 寛之さんの記事があります。
ドラゴン堀江で堀江貴文さんに講師として共演していた教育系YouTuberのヨビノリたくみさんとの動画「数学を学ぶことのメリットとその魅力【ヨビノリたくみ×堀江貴文】 - Youtube」の中で、堀江貴文さんがなぜ2乗をするのかという質問に対し、たくみさんが積分の次数の話をしてちょっとだけ説明しています。
今回、自分なりに2乗について調べてまとめてみました。
2乗が現れる数式
数学と統計と物理で2乗が現れる数式の一部
数学
正方形の面積
$S=a^2$
円の面積
$S=\pi r^2$
球の表面積
$S=４\pi r^2$
円の方程式
$(x-a)^2+(y-b)^2=r^2$
球面の方程式
$(x-a)^2+(y-b)^2+(z-c)=r^2$
ピタゴラスの定理
$a^2 = b^2 + c^2$
1 から 2n − 1 までの n 個の奇数の総和は n2 に等しい
$\displaystyle \sum_{k=1}^{n}(2k-1)=n^{2}$
三角関数の重要公式
$sin^2 + cos^2 = 1$
余弦定理
$a^2 = b^2 + c^2 − 2bc\cos A$
$b^2 = c^2 + a^2 − 2ca\cos B$
$c^2 = a^2 + b^2 − 2ab\cos C$
虚数
$i^2= -1$
0 を除く平方数の逆数和 バーゼル問題
$\displaystyle \sum_{k=1}^{\infty}\frac {1}{k^{2}}=\frac{\pi^{2}}{6}$
統計
標準偏差
$\displaystyle \sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}$
最小二乗法
$\displaystyle \sum_{i=1}^{n}(x_{i} - m)^{2}$
正規分布
$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$
カイ2乗分布
$\displaystyle X^2=\sum_{i=1}^{r}{\frac{(n_{i}-E_{i})^2}{E_{i}}}$
物理
等加速度直線運動 変位
$\displaystyle x=v_0t + \frac{1}{2}at^{2}$
運動エネルギー
$\displaystyle K=\frac{1}{2}mv^{2}$
弾性力により位置エネルギー
$\displaystyle U=\frac{1}{2}kx^{2}$
質量エネルギーの式
$E＝mc^2$
光の強さ、音の強さ
$\displaystyle E=\frac {I}{r^2}$
万有引力の法則
$\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}$
クーロンの法則
$\displaystyle F=k{\frac {q_{1}q_{2}}{r^{2}}}$
2乗する意味
同じ数を2回掛けることを2乗といい日本語で「平方」ともいい、2乗した数には「平方数」という名称が与えられている。ちなみに英語では2乗のことはsquare(スクエア)ですね。
$2$ という数は最小の素数でもあります。3より大きい自然数は、$(2+x)$の形式で表すことが出来ます。
例 $3=2+1$、$4=2+2$、$5=2+2+1$、$7=2+2+2+1$
これは数式の3乗や4乗であっても2乗に分解して数式で表せるわけです。
面積
同じ数を2回掛けると何が求まるのか？
$1 \times 1=1$、$2 \times 2=4$、$3 \times 3=9$、$4 \times 4=16$、$5 \times 5=25$
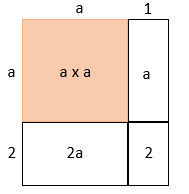
図形で考えれば、正方形の面積を求めることが出来ます。
長方形の面積を求める式は「たて×よこ」ですが、式を変形すれば正方形の面積(平方数)に加算か減算しても求めることが出来ます。
長方形の面積 たて $5$、よこ $4$ 、面積 $5\times4=20$
平方$3$ とした場合、$(3+2)(3+1)=3^2+3\times1+2\times3+2\times1=9+3+6+2=20$ と同じ結果となります。
一般式 $(a+2)(a+1)=a^2+3a+2$
円の面積は円を細かく刻んで長方形の形にした場合、たてが半径、よこが半径×πで「半径×(半径×π)」となり数式上は$\pi r^2$にまとめられる。
ご質問に対する返答動画です。円の面積はなぜπｒ＾２ - 鈴木貫太郎 Youtube
中学数学からはじめる微分積分 円の面積 - ヨビノリ Youtube
球の体積、表面積 中学生にも納得のいく方法で。 積分でも出します - 鈴木貫太郎 Youtube
ピタゴラスの定理
ピタゴラスの定理(三平方の定理)は、直角三角形の3辺の長さの関係を表します。
直角三角形の斜辺を1辺とする正方形の面積は他の2辺をそれぞれ1辺とする正方形の面積の和に等しい。
$a^2 + b^2 = c^2$ 例 $4^2 + 3^2 = 5^2$
※ピタゴラス数は$3,4,5$以外にも、$5,12,13$や$8,15,17$など無数にある。
「三平方の定理」がひと目で分かる展示が面白いと話題に 「視覚的にわかる」「こういうのが学校にあったら」
平方数のグノモン分解
連続する奇数の合計は必ず平方数となる。
例えば
$1=1^2$
$1+3=4=2^2$
$1+3+5=9=3^2$
$1+3+5+7=16=4^2$
$1+3+5+7+9=25=5^2$
これを数式にしたのが下記の式となります。
$\displaystyle \sum_{k=1}^{n}(2k-1)=n^{2}$
図で表してみます。●で作った正方形を「くの字」に区切ると、奇数が頭に現れる。
ピタゴラス数を得る方法
$1+3+5+7+9=25=5^2$
$→最後の9は3^2$に変更
$1+3+5+7+3^2=5^2$
$→1\cdots7の合計16は4^2$に変更
$4^2+3^2=5^2$
$1+3+5+7+\cdots+23+25=169=13^2$
$→最後の25は5^2$に変更
$1+3+5+7+\cdots+23+5^2=13^2$
$→1\cdots23の合計144は12^2$に変更
$12^2+5^2=13^2$
※$8,15,17$ のように上記方法(グノモンの和)では得られないタイプのものもある。
グノモンの和の方法ですべてのピタゴラス数が作れるわけではない。
円の方程式
円の方程式 $(x-a)^2+(y-b)^2=r^2$ もピタゴラスの定理に関連しています。
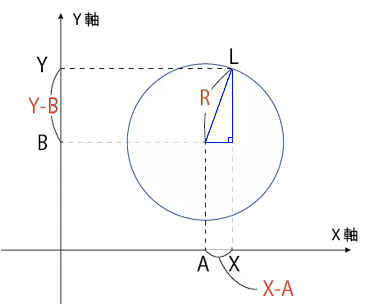
上図から分かるように、$R$ の長さは三平方の定理を使って
$R=\sqrt{(X-A)^2+(Y-B)^2}$
両辺を2乗すると・・ $(X-A)^2+(Y-B)^2=R^2$ となります。
球面の方程式 $(x-a)^2+(y-b)^2+(z-c)=r^2$ もこの応用です。
空間の球面の方程式
三角関数の重要公式
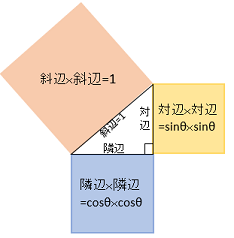
三角関数の重要公式の1つ $sin^2 + cos^2 = 1$ もピタゴラスの定理に関連しています。
三角関数は単位円(半径1の円)を基にしているので斜辺は$1$、対辺の長さ$sin$、隣辺の長さ$cos$の直角三角形になります。
余弦定理
ピタゴラスの定理は、直角三角形の3辺の長さの関係ですが、全ての三角形の3辺の長さの関係を表すのは余弦定理となります。考え方は先述した長方形の面積を正方形の面積に加算か減算して求めたのと一緒です。直角三角形に対して加算か減算して求める。
$a^2 = b^2 + c^2 − 2bc\cos A$
$b^2 = c^2 + a^2 − 2ca\cos B$
$c^2 = a^2 + b^2 − 2ab\cos C$
虚数
虚数($i=\sqrt{-1}$)はもともと解を求めた際に便宜上出てきてしまう答えに名前を付けたものでした。だから虚数が発見されてから数百年間は「詭弁的な数字であり、実用性はない」「ただの想像上の数に過ぎない」と否定的に評価されていたのです。
例えば $x^2-4=0$ は、$x^2=4$ となり、2乗したら$4$であり解は$-2$と$2$です。これを数学の問題文としては符号を逆にすることも可能なわけです。
$x^2+4=0$ は、$x^2=-4$ となり、2乗したら$-4$になるわけです。解には虚数$i$を付けて $-2i$ と $2i$ となります。
レオンハルト・オイラーが虚数のもつ重要性を解き明かした後、その評価は一変します。
なぜ、マイナス×マイナスはプラスなのか？ 負✕負＝正 虚数（複素数）を使って説明します - 鈴木貫太郎 Youtube
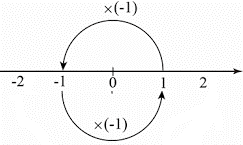
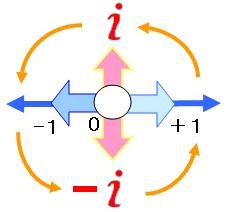
実数のマイナスとプラスの関係性を180度回転すると考えた場合、90度を表すのに虚数 $i$ を使います(複素数平面)。
$i^0=1、i^1=i、i^2=-1、i^3=-i、i^4=1 \cdots$ 90度として4回転でもとの$1$に戻る
バーゼル問題
$0$ を除く平方数の逆数和を求めると、何故が $\pi$ が現れる。
$\displaystyle \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots = \frac{\pi^2}{6}$
予備知識
2次方程式 $x^2-7x+10=0$ の解は $x=2、x=5$ を持っている。
$x^2-7x+10=(x-2)(x-5)$ と因数分解できる。
ちなみに下記のようにも因数分解でき、こちらのほうが今後の説明に役に立つ。
$\displaystyle x^2-7x+10=10\left(1-\frac{x}{2}\right)\left(1-\frac{x}{5}\right)$
円周率の平方がなぜ現れるのか
$\sin \theta$ は円周率 $\pi$ の整数倍$(\cdots,-3\pi,-2\pi,-\pi,0,\pi,2\pi,3\pi,\cdots)$ を解としており、$\pi$ の整数倍を $\theta$ に代入すると $0$ になる。
サイン関数のテーラー展開式は下記となる。
$\displaystyle \sin \theta=\frac{1}{1!}\theta-\frac{1}{3!}\theta^{3}+\frac{1}{5!}\theta^{5}-\cdots$
これに先述した円周率 $\pi$ の整数倍を当てはめる。
$\displaystyle \sin \theta=\cdots\left(1+\frac{\theta}{3\pi}\right)\left(1+\frac{\theta}{2\pi}\right)\left(1+\frac{\theta}{1\pi}\right)\theta\left(1-\frac{\theta}{1\pi}\right)\left(1-\frac{\theta}{2\pi}\right)\left(1-\frac{\theta}{3\pi}\right)\cdots$
実際、$\theta=3\pi$ のとき、$\displaystyle \left(1-\frac{\theta}{3\pi}\right)$の結果は $0$ になり、$\theta=-2\pi$ のとき、$\displaystyle \left(1+\frac{\theta}{2\pi}\right)$ でも $0$ になります。
分母が同じ2つの式を掛け合わせると、例えば下記のようになる。
$\displaystyle \left(1+\frac{\theta}{3\pi}\right)\left(1-\frac{\theta}{3\pi}\right)=1-\frac{\theta^{2}}{3^{2}\pi^{2}}$
したがって、$\sin \theta$ は下記のように表現できる。
$\displaystyle \sin \theta=\theta \left(1-\frac{\theta^{2}}{1^{2}\pi^{2}}\right)\left(1-\frac{\theta^{2}}{2^{2}\pi^{2}}\right)\left(1-\frac{\theta^{2}}{3^{2}\pi^{2}}\right)\cdots$
これは冒頭の $\theta$ が必ず掛け算されるので、$\theta \times \theta^{2}=\theta^{3}$ となり、 $\theta^{3}$ の係数を求めることになります。
サイン関数のテーラー展開式に $\theta^{3}$ があるのが $\displaystyle -\frac{1}{3!}\theta^{3}$ なので、これを使用します。
分母の $3!$ は、$3\times2\times1=6$ です。
$\theta^{3}$の係数は、$\displaystyle -\frac{1}{1^2\pi^2}-\frac{1}{2^2\pi^2}-\frac{1}{3^2\pi^2}-\frac{1}{4^2\pi^2}-\cdots=-\frac{1}{6}$ が得られ
両辺に $(-1)$ と $\pi^2$ を掛ければ、念願の下記の式が得られます。
$\displaystyle \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots = \frac{\pi^2}{6}$
円周率が現れるのは、サイン関数を $0$ にする値が $(整数) \times (円周率)$ だからである。円周率の2乗になるのは、$(整数) \times (円周率)$ がそれぞれプラスとマイナスで2回現れるからである。そして平方数の逆数和が生まれるのも同じ理由。
別解：中学数学でバーゼル問題（自然数の逆数の平方和）の答えに円周率が出る理由を解説 タマキの数学 Youtube
平方数の逆数和が素数と関係する
オイラーは平方数の逆数和が円周率と関係するのを突き止めたあと、平方数の逆数和が素数と関係することも発見した。
(自然数全体に関する和) = (素数全体に関する積)
$\displaystyle \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\cdots = \frac{2^2}{2^2-1}\times\frac{3^2}{3^2-1}\times\frac{5^2}{5^2-1}\times\frac{7^2}{7^2-1}\times\cdots$
オイラー積の数式
1 とおいたとき
$\displaystyle \sum_{n=1}^{\infty}{\frac {1}{n^{s}}}=\prod_{p}{\frac{1}{1-1/p^{s}}} =\prod_{p}{\frac{1}{1-p^{-s}}}$ 上の式に合わせるなら、$\displaystyle =\prod_{p}{\frac{p^{s}}{p^{s}-1}}$
成り立つポイントは素因数分解の一意性(2以上のすべての自然数は、素数の積に一通りに分解される)である。
例えば、$12$は$12=2^2\times3$ と分解され、$30$は$30=2\times3\times5$ と分解され、他の分解の仕方はない。
標準偏差と最小二乗法
標準偏差
$\displaystyle \sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}$
最小二乗法
$\displaystyle \sum_{i=1}^{n}(x_{i} - m)^{2}$
どちらも2乗する理由は同じで、2乗することで負数がなくなりすべて正数として扱えるためです。
正数にするなら絶対値でもいいのではないかという疑問がわくと思いますが、2乗にすると簡単に微分できるのに対し、絶対値の微分は面倒だったりします。その点でも2乗するのは利点があります。
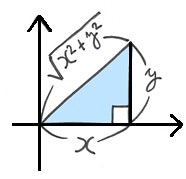
ピタゴラスの定理(三平方の定理)で直角三角形の斜辺の長さを求めるには $\sqrt{x^2+y^2}$ となります。つまり、データのばらつきとは、平均点からの距離を表しているため2乗するわけです。
正規分布
正規分布はガウス分布と呼ばれることもしばしばあります。これは18世紀から19世紀に渡って活躍した数学者C.F.ガウスに由来します。
| イメージ | 正規分布（ガウス分布） | 標準正規分布 |
|---|---|---|
 |
$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$ | $\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^{2}}{2}\right)$ |
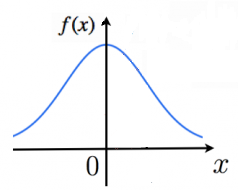
まず、世の中の多くの事象は平均値を取る確率が一番大きく、平均値から離れるにつれその値を取る確率は小さくなることが知られています。
このような現象を簡単に表せる関数 $f(x)=e^{−x^2}$ でした。
平均の値を変えるにはこのグラフを左右に動かす必要があります。そのため、式は $f(x)=e^{−(x−μ)^2}$ とします。このようにするとμの値によって左右にグラフを平行移動させることが出来ます。次に、グラフの幅を変えたい。そこで、$\displaystyle f(X)=e^{-\frac{(x−\mu)^2}{2\sigma^2}}$ と変形してみます。
正規分布の密度関数を意味的に理解する
マイナスが付いた exp( - x ) っていうのは、逆に半分の1/2、そのまた半分の1/4、そのまた半分の1/8、そのまた半分の1/16、ってだんだん減ってく形なの。正規分布の山の裾野が、富士山みたいにダラーッて減ってくのは、この exp( - x ) の形だね。
でも、ただ exp( - x ) だけだと、片っ方だけ、右側だけしか減らないよ。そこで、左右両側が同じように減りますようにって、出てきたのが x^2 。二乗ってすると、マイナスｘマイナス＝プラスだから、左右の形がはねっ返りで同じになるんだ。
正規分布は指数減衰と二乗からできている
曲線 $\displaystyle y=exp(-\frac{x^2}{2})$ が山なりの形で誤差分布に似ているので採用された。あとは倍率を合わせたり平行移動させたりするのがくっついている。
正規分布の中でも平均が $μ=0$、分散が $σ^2=1$ であるのが標準正規分布となり式が簡単になる。
正規分布の基礎的な知識まとめ
係数に円周率 $\pi$ の平方根が使われているのは、「全確率が $1$ となる」ように調整するためにすぎないです。
例 標準正規分布の下表の合計値は $1$ になります。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 0.0045 | 0.0546 | 0.242 | 0.398 | 0.242 | 0.0546 | 0.0045 |
円周率の平方根について下記の動画が参考になる。
カイ2乗分布
$\displaystyle X^2=\sum_{i=1}^{r}{\frac{(n_{i}-E_{i})^2}{E_{i}}}$
観測データと期待度数のズレを2乗したものを期待度数で割る
カイ二乗分布は複数の独立な標準正規分布によって得られます。
2乗するのは標準偏差と最小二乗法で書いたのと同じ理由です。
平方和
平方和は「個々のデータと基準値(例 平均値)の差を二乗した値の和」のことで、統計学の基本計算と言っていい。
データが全体的にどの程度ばらついているかを表します。
- 平方和が大きいとばらつきが大きい
- 平方和が小さいとばらつきが小さい
各IDの数学の点数から平均値の81を減算します。
| ID | 点数 | 偏差 |
|---|---|---|
| 1 | 96 | 96-81= 15 |
| 2 | 63 | 63-81= -18 |
| 3 | 85 | 85-81= 4 |
| 4 | 66 | 66-81= -15 |
| 5 | 91 | 91-81= 10 |
| 6 | 89 | 89-81= 8 |
| 7 | 77 | 77-81= -4 |
偏差をそれぞれ2乗して総和を求めます。
| ID | 偏差 | 偏差^2 |
|---|---|---|
| 1 | 15 | 15^2 = 225 |
| 2 | -18 | -18^2 = 324 |
| 3 | 4 | 4^2 = 16 |
| 4 | -15 | -15^2= 225 |
| 5 | 10 | 10^2 = 100 |
| 6 | 8 | 8^2 = 64 |
| 7 | -4 | -4^2 = 16 |
総和は $225+324+16+225+100+64+16=970$ となります。
ちなみに2乗しないまま総和すると、$15−18+4−15+10+8−4=0$と値が $0$ になってしまいます。
等加速度直線運動 変位
$\displaystyle x=v_0t + \frac{1}{2}at^{2}$
落体法則
ガリレオはまた、落体の法則を発見した。この法則はおもに2つからなる。1つ目は、物体が自由落下するときの時間は、落下する物体の質量には依存しないということである。2つ目は、物体が落下するときに落ちる距離は、落下時間の2乗に比例するというものである
ガリレオ・ガリレイ Wiki
当時ストップウォッチなどがない中で、どのようにして落下時間の2乗に比例すること検証したのか？
説①：人間の聴覚とりわけリズム感を利用したのです。それには上述した「グノモン」の考えを取り入れました。
下図のようなゆるい坂を作って坂道に複数の鈴をぶら下げた際、一番目の鈴と二番目の鈴の間隔を$1$としたとき、二番目の鈴と三番目の鈴の間隔が$3$、三番目の鈴と五番目の鈴の間隔が$5$、四番目の鈴と五番目の鈴の間隔が$7$、・・・という具合に間隔の比が連続する奇数になるように設置した。
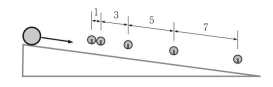
これで金属球を落下させる。金属球が鈴とぶつかると鈴が鳴る。鈴の音は規則正しく一定間隔のリズムに聞こえる。
説②：水時計を利用した。球を転がし始めると同時に、蛇口を開けて水を流し始め、1回鈴が鳴った時に蛇口を閉め溜まった水の量を測定します。2回鈴が鳴った時、3回の時・・・というように水の量を測定します。水の量は蛇口を開けてから閉じるまでの時間に比例しますので、短い時間を正確に測るストップウォッチの役目をしたと考えられる。
このような実験により緩い坂道を落ちる金属球の運動は「等速度」ではなく「等加速度」運動であることをガリレオは突き止めたのである。さらにガリレオは坂道を落ちる運動が「重さとは無関係であること」、そして「坂の傾斜を変えても、等加速度運動であるという性質は変わらないこと」を確認した。
等加速度運動
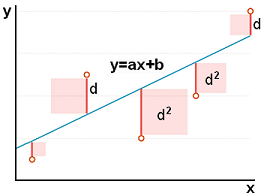
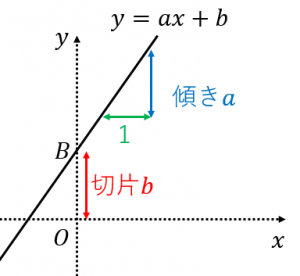
前提知識として、1次方程式 $y=ax+b$ は下図のように傾き$ax$、切片$b$となります。
はじきの法則
下左図の等速度運動はずっと同じ速度です。はじきの法則に従えば、一定の速度$v$で経過時間$t$に進む距離$vt$は「長方形の面積」に表される。
下右図の等加速度運動は徐々に速度が変化します。そのため、はじきの法則は使えなくなります。
先程の1次方程式 $y=ax+b$ に当てはめてみると傾きは $at$ となります。等速度運動と同様に面積を求めるとすると三角形 $OAB$ の面積を求めることになり $\displaystyle (底辺)\times(高さ)\div 2 = t \times at \div 2=\frac{1}{2}at^2$ となります。
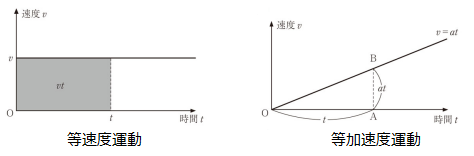
そして切片 $b$ にあたるのが初速度 $v_0t$ (長方形の面積)と三角形の面積 $\displaystyle\frac{1}{2}at^2$ を足すと台形の面積が求まります。
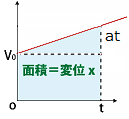$\displaystyle x=v_0t + \frac{1}{2}at^{2}$
変化していく面積を求めるという考え方は「積分」になるわけです。
台形の面積の公式 $(上底+下底) \times 高さ \div 2$ を使用した場合
台形という図形の形と面積を求める公式
$x = (v_0 + (v_0 + at)) \times t \div 2$
$x = (v_0t + v_0t + at^2) \div 2$
$x = (2v_0t + at^2) \div 2$
$\displaystyle x=v_0t + \frac{1}{2}at^{2}$
等加速度運動の時間tを含まない式
$v=v_0+at$ より、$\displaystyle t = \frac{(v - v_0)}{a}$です。
これを $\displaystyle x=v_0t + \frac{1}{2}at^{2}$ に代入します。
$x=\displaystyle \frac{(v-v_0)^2}{2a} + \frac{v_0(v-v_0)}{a}$
$x=\displaystyle \frac{(v^2-2v_0v+v_0^2)}{2a} + \frac{2(v_0v-v_0^2)}{2a}$
$x=\displaystyle \frac{(v^2-2v_0v+v_0^2+2v_0v-2v_0^2)}{2a}$
$x=\displaystyle \frac{(v^2-v_0^2)}{2a}$
すると、$v^2 – v_0^2 = 2ax$ が得られます。
積分の次数の話
ヨビノリたくみさんが、堀江貴文さんの「なぜ2乗をするのか」という質問に対し、たくみさんが積分の次数の話をしています。
数学を学ぶことのメリットとその魅力【ヨビノリたくみ×堀江貴文】 - Youtube」
積分のときは「次数を上げて、次数を分母に置く」、微分のときは「前に出して、1次下げる」というテクニックがあります。
1次式 $v=at$ を積分した場合、次数を上げて次数を分母に置くことになるので、$\displaystyle \frac{1}{2}at^{2}$ となります。
運動エネルギー
$\displaystyle K=\frac{1}{2}mv^{2}$
※運動エネルギーの $K$ は、英語表記であるKinetic Energyから来ています。
鉄球をボーリングのように転がして車に衝突させることを考えてみましょう。鉄球が衝突すると車は破壊・変形されます。つまり動いている鉄球というのはそれだけでエネルギーを持っているということ。
鉄球の破壊力を大きくするには
- より質量の大きな鉄球で衝突させる
- 質量は変えずに速さを大きくして衝突させる
このように動いている鉄球の持つエネルギーは「質量」と「速さ」によって変化します。「速さ＝その物体の動き」によって決まるエネルギーなので、これを運動エネルギーと言います。
運動エネルギーは質量に比例・速さの2乗に比例します。
力$F$は運動方程式を用いると、$F=ma$ と変換する事が出来ます。
加速度 $a$ は $F=ma$ より、$\displaystyle a=\frac{F}{m}$ となります。
等加速度運動の時間 $t$ を含まない式「$v^2 – v_0^2 = 2ax$」は、初速度 $v0$ から速度が $v$ になったときの式です。
最初の速度を $v_0=v$、最終的に止まったときの速度 $v=0$、加速度 $\displaystyle \frac{F}{m}$
これらを代入して求めると
$\displaystyle v^2=2\left(\frac{F}{m}\right)x$
$\displaystyle v^2=\frac{2F}{m}x$
$\displaystyle Fx=\frac{1}{2}mv^2$
運動エネルギーは、$\displaystyle K=\frac{1}{2}mv^{2}$ になります。
弾性力により位置エネルギー
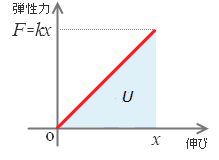
$\displaystyle U=\frac{1}{2}kx^{2}$
等加速度運動と考え方は同じで、三角形の面積を求めます。
質量エネルギーの式
$E＝mc^2$
アルベルト・アインシュタインの有名な式です。
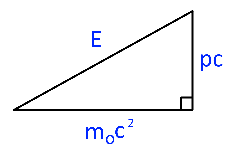
$E^2=(m_0c^2)^2+(pc)^2$
$E$：総エネルギー（Total Energy）
$m_0c^2$：静止エネルギー（Rest Energy）
$pc$：運動エネルギー（Momentum Energy）
$m_0$は静止質量、$p$は運動量、$c$は光の速さ
各々のエネルギーは、$E = m_0c^2 + pc$ という直線的な関係ではなく、
$E^2=(m_0c^2)^2+(pc)^2$ という直角三角形の関係にあるというのが相対性理論的な考え方です。
上の式を使って静止している物体のエネルギーを考えたとき、運動量 $p=0$ とすれば $E＝mc^2$ となる。
$mc^2$ の2乗の部分は、$x^2+y^2+z^2=(ct)^2$ と球面の方程式に関連しています。
距離の二乗に反比例
逆二乗則に従うもの
光の強さ、音の強さ
$\displaystyle E=\frac {F}{S}=\frac {4{\pi}I}{4{\pi}r^2}=\frac {I}{r^2}$
万有引力の法則
$\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}$
クーロンの法則
$\displaystyle F=k{\frac {q_{1}q_{2}}{r^{2}}}$
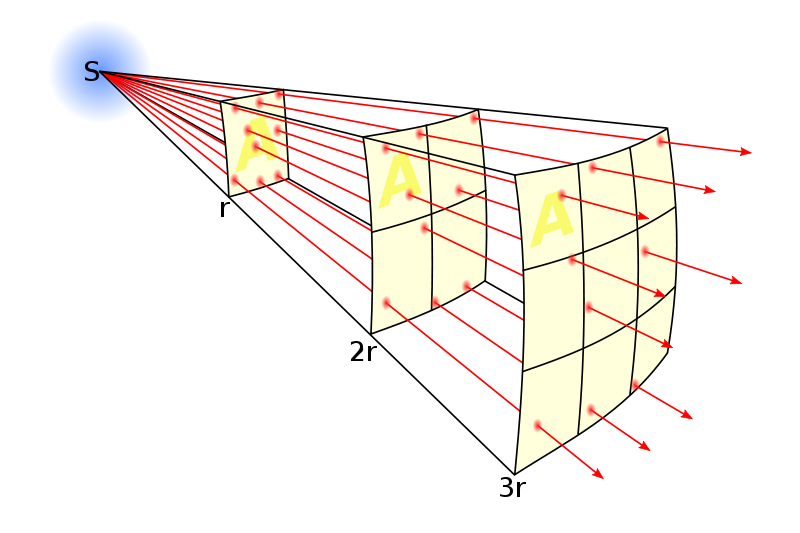
ある点から全方位に偏り無く影響力を及ぼすものがあるとき、その影響力は発生源からの距離の2乗に反比例します。球面の表面積は、半径が $r$ であるとき、$4{\pi}r^2$ です。半径が2倍になると球面の表面積は4倍、半径が3倍になると球面の表面積は9倍になります。発生源から全方位に偏り無く1万本の矢が放射されているとすると、半径2倍の球面においても1万本の矢が貫通し、半径3倍の球面においても1万本の矢が貫通しています。
そうしますと、半径2倍の球面を貫く矢の密度は $\displaystyle \frac{1}{4}$ になり、半径3倍の球面を貫く矢の密度は $\displaystyle \frac{1}{9}$ になります。
これが「影響力が発生源からの距離の2乗に反比例する」という意味です。
空間が３次元のため球の表面積 $S=4{\pi}r^2$ により２乗ですが、もし４次元なら３乗、5次元なら４乗となります。
最後に
これを調べる前は数学の2乗と物理の2乗はたまたま偶然に一緒になったのかと思っていたのですが、積分の考えを使えば数学と結びつくのかと思った次第です。
ピタゴラスの定理(三平方の定理)はとても重要で2乗のもとですね。負数をなくすために絶対値を使用しないで2乗を使用するのは微分がしやすくなることもあるが、距離を求める要素も含んでいる。
紹介した以外にはも2乗を使用した式は幾つもあると思います。なぜ2乗するのかという素朴な疑問から調べ始めたのですが、もともと数学や物理は苦手なので限界がありますね。また時間が経って理解が進めば追記していきます。