はじめに
話題の BitNet b1.58 の記事で「この技術によりGPUが不要になるかもしれない、NVIDIAなどの半導体関係の株価が...」となっていました。
その関連でいろいろ調べていくと、バイナリ乗算はXNORに置き換え可能というのが自分の中で最初に引っ掛かりました。
XNORとは
論理回路である、XNOR(排他的論理和 XORの否定)は、同じ値 1、違う値 0 になります。
| 入力A | 入力B | 出力X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
XNORゲートは1ビット加算器として機能する。すなわち、2つのビットを加算した結果の1ビット目が得られる。2ビット目の桁上がり(キャリー)は加算する2つのビットが1の時であるからANDゲートによって得られる。したがってXNORゲートとANDゲートを使って半加算器を構成できる。
XNORゲート - wikipedia
バイナリ乗算とは
バイナリは0と1の1bitで掛け算(A * B)すると下記の結果となります。
結果を見ると、XNORとは 0 * 0 のところが一致しません。
| 入力A | 入力B | A * B | A XNOR B |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
では、バイナリ乗算がXNORに置き換え可能とはどういうことなのでしょうか?
バイナリ値を0と1ではなく、-1と1に置き換えてみましょう。
| 入力A | 入力B | A * B | A XNOR B |
|---|---|---|---|
| -1 | -1 | 1 | 1 |
| -1 | 1 | -1 | 0 |
| 1 | -1 | -1 | 0 |
| 1 | 1 | 1 | 1 |
A * Bの結果である-1を0に置き換えると、XNORと同じ結果になります。
これを利用することで簡単な計算に置き換えることが出来ます。
参照:ニューラルネットの1bit化 / 1bit-neural-network
XNOR-Net1の論文
重みと入出力をどちらも(-1,1)しかとらない二値とし,全ての-1 を回路上では 0 と置き換えることで,乗算を XNOR回路で実現する.従来最も回路規模を小さくすることができる手法とされている
他にも
Ternary Sparse XNOR-Net2の論文
XNOR-Netと三値化を組み合わせた手法である、入力は(1,-1)で重みは(-1,0,1)を取る。
内積
AIは内積計算だらけです。内積は主に2つのベクトルの“近さ”を表すのに使用されます。
例えば、手書き数字認識でどの数字か分類できるのは、より似ているかで判断しています。
方向が似ているベクトルを「似ている」と判断するなら、2つのベクトルが似ていると内積は大きくなるのです。

内積のいいところは何次元のベクトルであっても計算することができるところです。
2つのベクトル v1=(2, -1, 2)、v2=(3, -2, 1) があった場合、内積の計算方法と値は次のようになります。
$2 \times 3 + (-1) \times (-2) + 2 \times 1 = 10$
v1 = [2, -1, 2]
v2 = [3, -2, 1]
v_dot = 0
for x, y in zip(v1,v2):
v_dot += x * y
print (v_dot) # 出力 10
バイナリの内積
2つの4bitベクトル v1=(1, 0, 1, 1)、v2=(1, 1, 0, 1) を考えます。
bitと書いているのに配列としているのは、説明向けの擬似のため。
XNOR-Net1の論文にあるように、(-1,1)しかとらない二値の全ての -1 を 0 と置き換える処理を内積計算前にしておく必要がある。
v1 = [1, 0, 1, 1]
v2 = [1, 1, 0, 1]
v_dot = 0
for x, y in zip(v1,v2):
v_dot += x * y
print (v_dot) # 出力 2
通常の計算をXNORによる計算に置き換えて、最後に類似度まで求めてみます。
def xnor(A, B):
return 1 if not ( (A!=0) ^ (B!=0) ) else 0
v1 = [1, 0, 1, 1]
v2 = [1, 1, 0, 1]
result = list(map(xnor, v1, v2))
print (result) # 出力 [1, 0, 0, 1]
# ポピュレーションカウントを計算
xnor_dot = sum(result)
print (xnor_dot) # 出力 1 + 0 + 0 + 1 = 2
# 正規化としてビット長で割ります。 今回のビット長は4ビット
# 類似度
similarity = xnor_dot / len(v1);
print (similarity) # 出力 0.5
内積の値を求めるのにsumしていますが、1の数を数えても同じ結果になります。
POPCNT(ポピュレーションカウント)
2008年から2009年あたりに、AMDやIntelがCPUにPOPCNT命令を実装しています。
POPCNT命令は、値を2進数に展開し1の出現回数を返してくれるコマンドになります。
バイナリの内積においてハードウェアであるCPUに専用命令があるわけですから、計算速度がより上がります。
バイナリの内積(bit演算)
ビットカウントのPyhton実装を見つけたので、bit演算で組んでみました。
def popcount(x):
'''xの立っているビット数をカウントする関数
(xは64bit整数)'''
# 2bitごとの組に分け、立っているビット数を2bitで表現する
x = x - ((x >> 1) & 0x5555555555555555)
# 4bit整数に 上位2bit + 下位2bit を計算した値を入れる
x = (x & 0x3333333333333333) + ((x >> 2) & 0x3333333333333333)
x = (x + (x >> 4)) & 0x0f0f0f0f0f0f0f0f # 8bitごと
x = x + (x >> 8) # 16bitごと
x = x + (x >> 16) # 32bitごと
x = x + (x >> 32) # 64bitごと = 全部の合計
return x & 0x0000007f
def xnor(A, B):
return ~(A ^ B) & 0x0F
v1 = 0b1011
v2 = 0b1101
result = xnor(v1, v2)
# ポピュレーションカウントを計算
xnor_dot = popcount(result)
print (xnor_dot) # 2
# 正規化としてビット長で割ります。 今回のビット長は4ビット
# 類似度
similarity = xnor_dot / 4;
print (similarity) # 0.5
その他
本題とズレるが、関連で調べている時に知ったこと
かけ算が不要の理解
自分は BitNet b1.58 の記事でGPUが不要になるかもしれないの理解がすぐに出来ませんでした。しかし、下図を見てようやく理解できました。
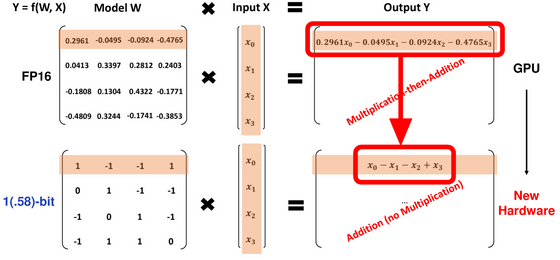
従来のモデルであれば入力に対して「0.2961」などのウェイトをかけ算してから足し引きする必要がありましたが、「-1」「0」「1」の3値のみであればかけ算が不要になり、全ての計算を足し算で行えるようになります。
実際には、最終段階で「-1」「0」「1」の3値を使用するのであって、全ての重みを「-1」「0」「1」の3値のみにしてしまうと損失関数(Loss)の値が下がらなくて精度が出なくなってしまう。
最も近い2の冪乗で近似値を重みに使う
対数量子化は、浮動小数点を 2 のべき乗で近似した固定小数点にすることで積演算をシフト演算で代用することが可能になるので、精度はやや劣るがリソース使用量を大きく削減することができる。
ローカルLLMに向き合う会
「ローカルLLMに向き合う会」というコミュニティであることを知って、今回 Discord に参加しました。
最後に
昔にベーマガを読んでいた時に、当時はメモリが少なかったから、sin や cos を 256 で割った値を配列に格納しておいて高速化した技術があったなと思い出しました。ゲームなのでそこまで精度は必要なかった。
時代こそ変わりゲームから人工知能になったが、高速化と少ないメモリで実現させようといろいろなアイディアがうまれるのはいいことですよね。