概要
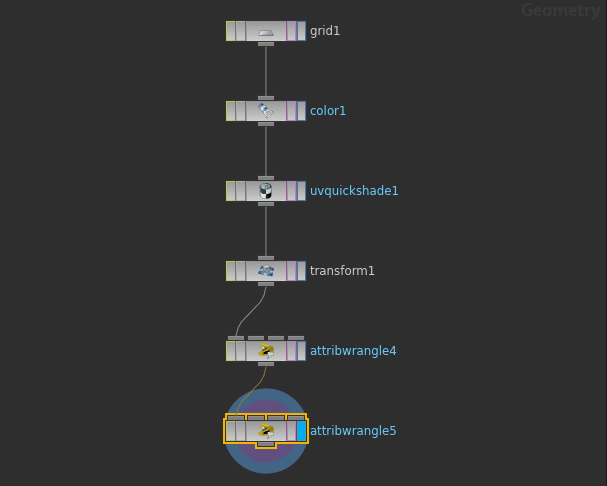
HoudiniのWrangleで平面を球や円錐に変形して、エフェクト用のメッシュを作成します。頂点の位置を計算で直接変更しているだけなので他の3Dソフトやコードでも使えると思います。もとの平面は0<x<1, 0<z<1のものを使います。Gridを使用し、Sizeを1*1にし、Transformでx,zを+0.5して、0<x<1, 0<z<1の平面を用意します。
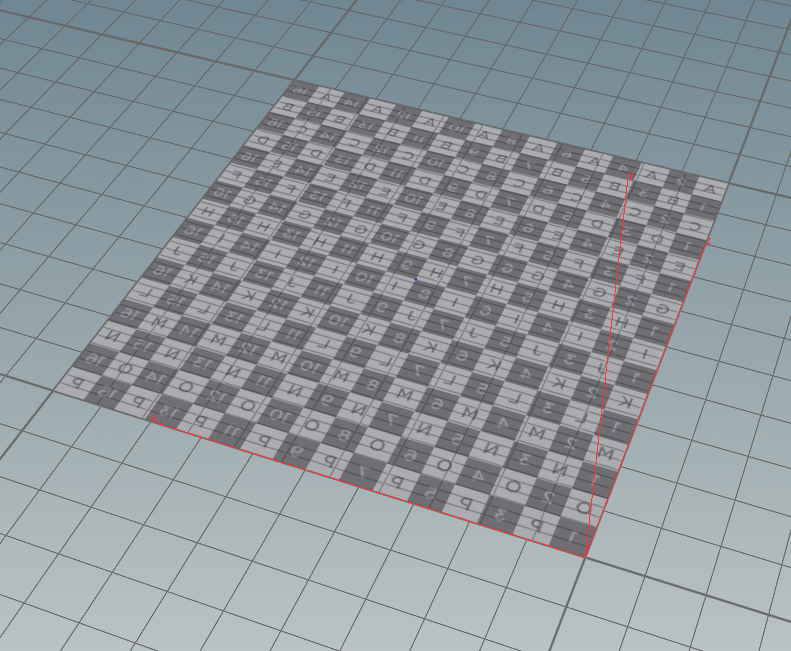
※例ではわかりやすくするため間にUVQuickShadeを挟んでいます。
※書いていたときのミス防止のため、助長に変数を使っています(in, outなど)
球
球面座標上に平面を投影します。Wikipedia-極座標系

vector in = @P;
float r = 1.0;
vector out;
float angle1 = lerp(0.0, 2.0 * $PI, in.z);
float angle2 = lerp(0.0, $PI, in.x);
out.x = r * cos(angle1) * sin(angle2);
out.z = r * sin(angle1) * sin(angle2);
out.y = r * cos(angle2);
@P = out;
上端と下端を切り取った球
vector in = @P;
float r = 1.0;
vector out;
float angle1 = lerp(-$PI, $PI, in.z) ;
float angle2 = lerp(0.3 * $PI, (1.0-0.3) * $PI, in.x);
out.x = r * cos(angle1) * sin(angle2);
out.z = r * sin(angle1) * sin(angle2);
out.y = r * cos(angle2);
@P = out;
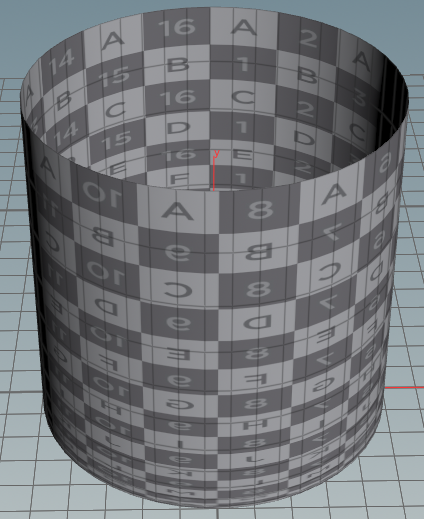
チューブ
円柱座標に平面を投影します。Wikipedia-極座標系

vector in = @P;
float r = 0.5;
float height = 1.0;
float angle = 2.0 * $PI * in.x;
vector out;
out.x = r * cos(angle);
out.y = height * in.z;
out.z = r * sin(angle);
@P = out;
ねじれたチューブ
vector in = @P;
float r = 0.5;
float height = 1.0;
float angle = 2.0 * $PI * in.x;
float rotate_rate = -0.2;
angle += 2.0 * $PI * rotate_rate * in.z;
vector out;
out.x = r * cos(angle);
out.y = height * in.z;
out.z = r * sin(angle);
@P = out;
頂点が下寄りのチューブ
vector in = @P;
float r = 0.5;
float height = 1.0;
float angle = 2.0 * $PI * in.x;
vector out;
out.x = r * cos(angle);
out.y = height * pow(in.z, 2.0);
out.z = r * sin(angle);
@P = out;
コーン
heightで全体の高さ、rのlerp関数のminで下端、maxで上端の半径を指定
vector in = @P;
float angle = lerp(0.0, 2.0 * $PI, in.x);
float height = 0.3;
float r = lerp(0.75, 1.0, in.z);
vector result;
result.x = r * cos(angle);
result.y = height * in.z;
result.z = r * sin(angle);
@P = result;
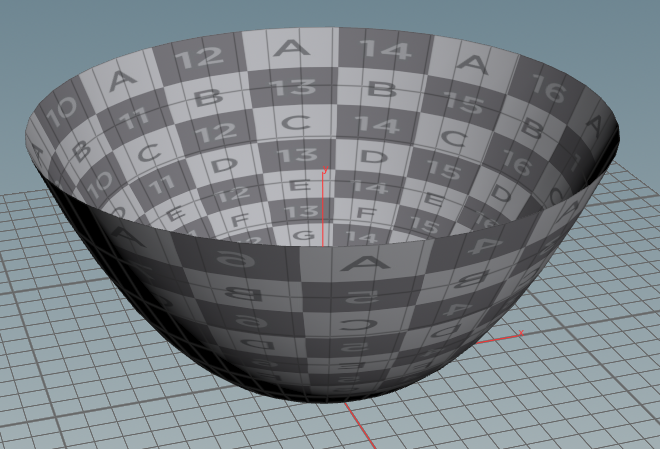
パラボラアンテナ
height式内のpowの係数、r式内のpowの係数により、形状の調整、頂点位置の調整ができます。
vector in = @P;
float rad = 2.0 * $PI * in.x;
float height = 1.0 * pow(in.z, 2.0 );
float r = 1.0 * pow(in.z, 1);
vector out;
out.x = r * cos(rad);
out.y = height;
out.z = r * sin(rad);
@P = out;
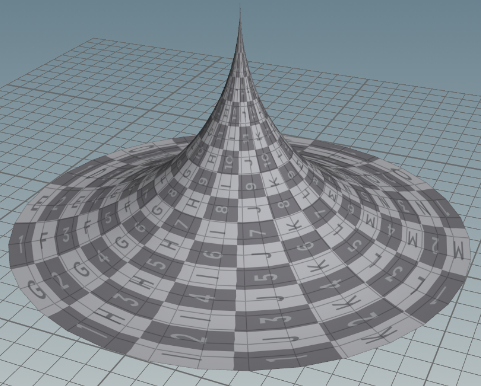
ブラックホール形状
vector in = @P;
float r = 1.0;
vector out;
float angle1 = lerp(-$PI, $PI, in.z) ;
float angle2 = lerp(0.0 * $PI, 0.5 * $PI, in.x);
out.x = r * cos(angle1) * (1.0 - sin(angle2));
out.z = r * sin(angle1) * (1.0 - sin(angle2));
out.y = r * (1.0 - cos(angle2));
@P = out;
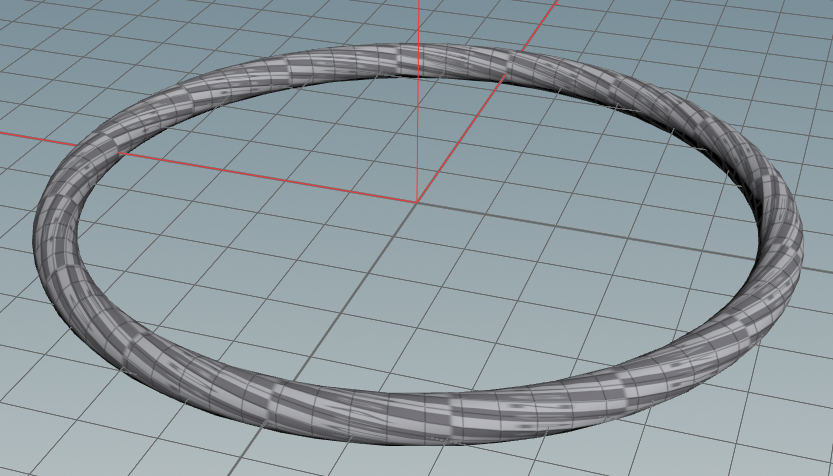
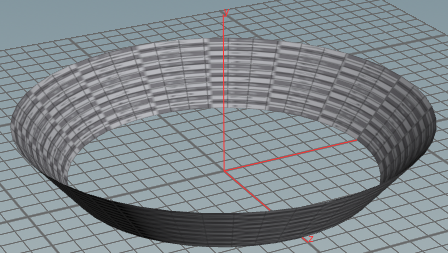
リング
vector in = @P;
float angle = lerp(2.0 * $PI, 0.0, in.x);
float r = lerp(0.5, 1.0, 1.0 * in.z);
vector out;
out.x = r * cos(angle);
out.z = r * sin(angle);
out.y = 0.0;
@P = out;
波打ったリング
vector in = @P;
vector out;
float rad = lerp(2.0 * $PI, 0.0, in.x);
int num = 6; // 波の数
float wave_height = 0.2; // 波の高さ
float r = lerp(0.8, 1.0, 1.0 * in.z) + lerp(0.0, 0.05, sin(rad));
out.x = r * cos(rad);
out.z = r * sin(rad);
out.y = wave_height * sin(rad * num);
@P = out;
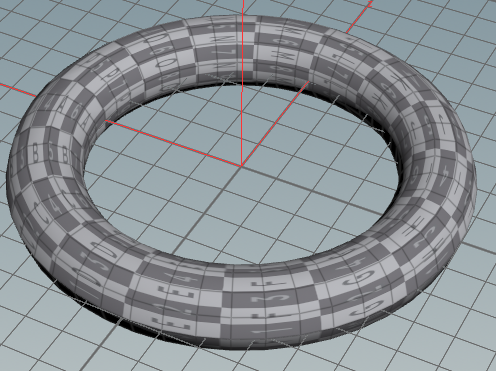
トーラス(ドーナツの形状)
一つのスクリプトだけでも作れますが、分けた見やすいので2つのWrangleに分けて書きました。この2つを連続でつなげてください。
一つ目のスクリプトのrがチューブの太さ、xに足した値d(今回は0.5)が全体の半径になります。
vector in = @P;
float r = 0.1;
float rad = 2.0 * $PI * in.x;
float d = 0.5;
vector out;
out.x = r * cos(rad) + d;
out.y = r * sin(rad);
out.z = in.z;
@P = out;
vector in = @P;
float r = in.x;
float rad = in.z * $PI * 2.0;
vector out;
out.x = r * cos(rad);
out.y = in.y;
out.z = r * sin(rad);
@P = out;
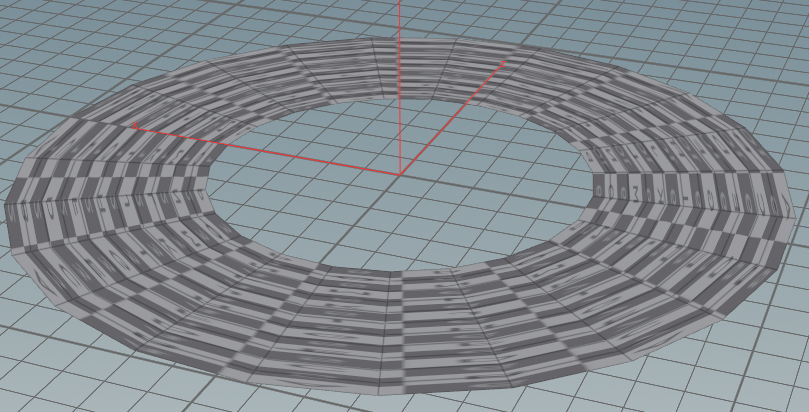
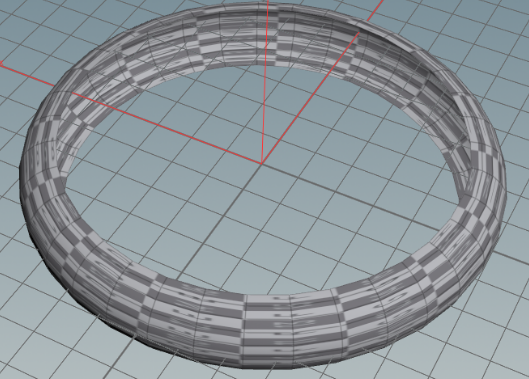
内側が欠けたトーラス
vector in = @P;
float r = 0.1;
float rad = lerp(-0.5 * $PI, 0.5 * $PI, in.x);
@P.x = r * cos(rad) + 0.5;
@P.y = r * sin(rad);
@P.z = @P.z;
vector in = @P;
float r = in.x;
float rad = 2.0 * $PI * in.z;
vector out;
out.x = r * cos(rad);
out.y = in.y;
out.z = r * sin(rad);
@P = out;
トーラス上にリボン
vector in = @P;
float r = 0.2; //トーラスの太さ(0 <r < 0.5)
float rad = 0.5 * $PI * in.x ;
float rotate_num = 8.0;
rad += rotate_num * 2.0 * $PI * @P.z;
@P.x = r * cos(rad) + 0.5;
@P.y = r * sin(rad);
@P.z = @P.z;
vector in = @P;
float r = in.x;
float rad = 2.0 * $PI * in.z;
vector out;
out.x = r * cos(rad);
out.y = in.y;
out.z = r * sin(rad);
@P = out;
ねじれたトーラス(ドーナツの形状)
twist_numでねじれ数を指定可能。
vector in = @P;
float r = 0.03;
float rad = 2.0 * $PI * in.x ;
float twist_num = 3.0; //ねじれ数
rad += twist_num * 2.0 * $PI * in.z;
vector out;
out.x = r * cos(rad) + 0.5;
out.y = r * sin(rad);
out.z = in.z;
@P = out;
vector in = @P;
float r = in.x;
float rad = 2.0 * $PI * in.z;
vector out;
out.x = r * cos(rad);
out.y = in.y;
out.z = r * sin(rad);
@P = out;
帯
vector in = @P;
float r = 0.1;
float height_rate = cos(lerp(-0.5 * $PI, 0.5 * $PI, in.z));
float rad = 1.0 * $PI * (in.x-0.5) * height_rate;
@P.x = r * cos(rad) + 0.5;
@P.y = r * sin(rad);
@P.z = in.z;
vector in = @P;
float r = in.x;
float rad = 1.0 * $PI * in.z;
@P.x = r * cos(rad);
@P.y = in.y;
@P.z = r * sin(rad);
スライダーで値を調整
これ以降のスクリプトは、chfを用いて係数をスライダーで変更可能にしています。
chfを含んだスクリプトを書いた後、以下のボタンを押すとスクリプト下に値を変更可能なスライダーが現れます。
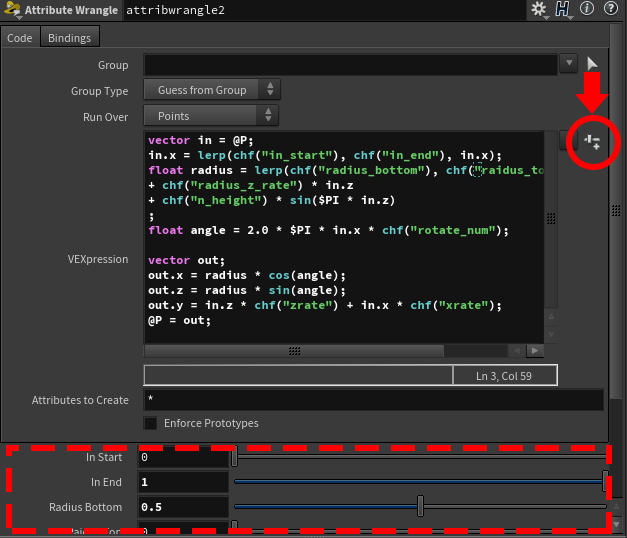
また、全ての係数の初期値が0なので、正しく設定しないと何も表示されないので注意してください。
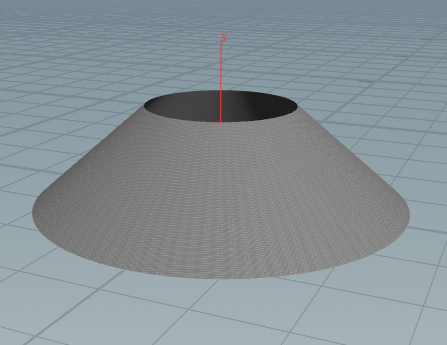
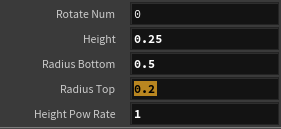
係数によってチューブにもリングにもできる形状
vector in = @P;
float rotate_num = chf("rotate_num");
float height = chf("height");
float radius_bottom = chf("radius_bottom");
float radius_top = chf("radius_top");
float radius = lerp(radius_bottom, radius_top, pow(in.z, chf("height_pow_rate")));
float angle = 2.0 * $PI * in.x
+ 2.0 * $PI * rotate_num * in.z;
vector out;
out.x = radius * cos(angle);
out.z = radius * sin(angle);
out.y = height * in.z;
@P = out;
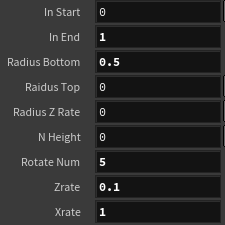
螺旋リボン
vector in = @P;
in.x = lerp(chf("in_start"), chf("in_end"), in.x);
float radius = lerp(chf("radius_bottom"), chf("raidus_top"), in.x)
+ chf("radius_z_rate") * in.z
+ chf("n_height") * sin($PI * in.z)
;
float angle = 2.0 * $PI * in.x * chf("rotate_num");
vector out;
out.x = radius * cos(angle);
out.z = radius * sin(angle);
out.y = in.z * chf("zrate") + in.x * chf("xrate");
@P = out;
エフェクト用メッシュとして使うために
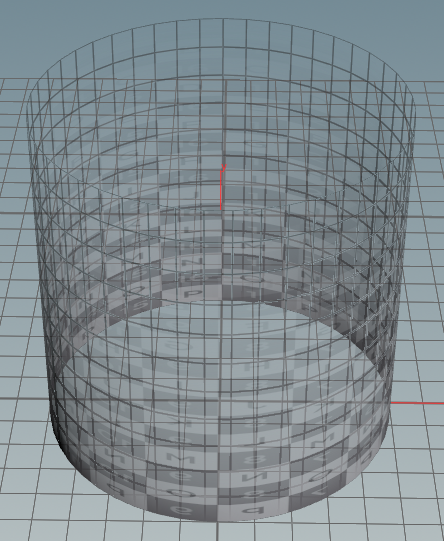
上記スクリプトでは書いていませんが、エフェクト用メッシュとして使う時は、各頂点のAlphaアトリビュートに適当な値を書き込んで出力してから使っています。(リングでは端に行くほど透明になる、チューブで上に行くほど透明になるなど)
FBXを出力する際にAlphaアトリビュートを書き込むには、間にColorを挟む必要があります。(不具合?)
vector in = @P;
float r = 0.5;
float height = 1.0;
float angle = 2.0 * $PI * in.x;
vector out;
out.x = r * cos(angle);
out.y = height * in.z;
out.z = r * sin(angle);
@P = out;
@Alpha = 1.0 - pow(@P.y, 0.5);
関連機能
SideFX LabsのCylinder Generator, Sphere Generator, Disc Generatorを使うことによって、UV付きのエフェクト用メッシュを作成することができます。
チュートリアル動画
SideFX Labs ツールリスト