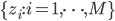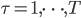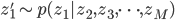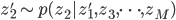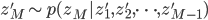はじめに
Machine Learning Advent Calendar 2012の2日目を担当させていただく@yag_aysです.機械学習ガチ勢の皆様に囲まれて非常にガクブル((((;゜Д゜)))しておりますが,少しでも何か皆さんの印象に残るような記事を書ければと思います.
今回の内容
今回は「パターン認識と機械学習」11章で紹介されているサンプリング法・MCMCの中でも,ギブスサンプリングについて取り上げたいと思います.1日目のnaoya_tさんがメトロポリス・ヘイスティング法について書かれており,偶然にも続き物のような形になりました.ギブスサンプリングは,メトロポリス・ヘイスティング法というおおまかな枠組みの中の特殊なケースです.とは言うものの,実際のアルゴリズムは外見上かなり違ったものになるので,メトロポリス・ヘイスティング法をあまり知らないという人でもこの記事は問題なく読むことができます.この記事では大雑把にギブスサンプリングの感覚を掴んでいただくという感じにしたいので,受理率が必ず1になるだとかエルゴート性や詳細平衡条件などの難しい内容は,PRMLを詳しく読んで頂くか本文の最後に載せる参考資料の方を当たって頂ければと思います.
今回の目標としては,PRML下巻P.259の図をお手本にして,二変量正規分布からのギブスサンプリングによる乱数生成を目指します.この図は概略図なうえにステップ数のオーダーといった抽象的な話になっていますが,少なくとも今回の記事を読めば,この図の楕円中央にあるクネクネした矢印が何を示しているのかは最低でも理解できると思います.それでは前置きはこのくらいにして,実際にアルゴリズムを確認してRでコードを書いてみましょう.
ギブスサンプリングのアルゴリズム
ギブスサンプリングは,条件付き分布からのサンプリングによって変数をどんどん置き換えていくという方法で,多次元の確率分布からのサンプリングを行います.
これだけでは何がなんだかという感じですが,ポイントとしては各ステップでは単に一つの変数
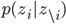
二変量正規分布からのギブスサンプリング
今回は,相関のある二変量正規分布からのギブスサンプリングを例に実験をしてみます.上で示したアルゴリズムでは多変量について扱っていましたが,今回は二変数のため変数の更新は交互に行います.
以下のコードでは,
- イテレーション回数:Niter
- 系列の初期値:x1, x2
- 二変量の相関:rho
として,forループの中で変数の更新を交互に行いながらマルコフ連鎖を生成しています.値を更新するコードを見ると,x1はx2の値を,x2はx1の値をといった形で,二変量の系列はお互いの値を使ってサンプリングしています.
Niter <- 5000
x1 <- 0
x2 <- 0
rho <- 0.7
for (i in 2:Niter){
x1[i] <- rnorm(1, rho*x2[i-1], sqrt(1-rho^2))
x2[i] <- rnorm(1, rho*x1[i], sqrt(1-rho^2))
}
plot(x1, x2, xlim=c(-5,5), ylim=c(-5,5), main="Gibbs sampling from a bivariate standard normal distribution")
このように結果をプロットしてみると,確かに相関のある二変量正規分布からサンプリングできていることが分かります.
サンプリング過程を可視化してみる
さて,とりあえずはギブスサンプリングを動かすことができたので,ここからはアルゴリズムの中で動いているサンプリングの過程について今回の例で詳しく見ていくことにしましょう.ポイントは,一つの変数をサンプリングで更新するときに,他の変数の値を固定するところにあります.
それではまず,上で示したコードのforループ内の値の更新を逐一プロットさせてみて,ギブスサンプリングの各ステップを可視化してみましょう.今回は,Rのanimationパッケージを用いて動画にしてみました.横軸と縦軸がそれぞれの変数に対応していて,図の中のマルがサンプリング結果の値を表しています.また,系列がどのように移動するのかを分かりやすくするために系列の値の間を直線で結んでいます.
(※ YouTubeのプレイヤーを埋め込めませんでした.以下のリンクをクリックしてYouTubeを開いてください)
すこし早いかもしれないので,もっとゆっくりバージョンのgifアニメもあります.
これをみると,系列の値の更新は必ず軸方向にしか移動しない,すなわち片方の値を固定した状態でもう一方の値を更新するという様子がはっきりとわかります.PRML下巻P.259の図の楕円中央に書かれていた矢印は,まさにこの過程を表していたんですね.
この動画の作成に用いたコードは以下の通りです.基本的な部分は前と同じですが,図の描写のためのコードを色々と加えています.
library(animation)
gibbs <- function(){
Niter <- 1000
x1 <- 0
x2 <- 0
rho <- 0.7
for (i in 2:Niter){
x1[i] <- rnorm(1,rho*x2[i-1],sqrt(1-rho^2))
plot(c(x1[1],rep(x1[2:i],each=2)[-(i-1)*2]), rep(x2[1:i-1],each=2),
col="gray", type="b",xlim=c(-5,5),ylim=c(-5,5), xlab="x1", ylab="x2")
lines(c(x1[i-1],x1[i]), c(x2[i-1],x2[i-1]), type="b", pch=19)
x2[i] <- rnorm(1,rho*x1[i], sqrt(1-rho^2))
plot(c(x1[1],rep(x1[2:i],each=2)), rep(x2[1:i],each=2)[-i*2],
col="gray", type="b",xlim=c(-5,5),ylim=c(-5,5), xlab="x1", ylab="x2")
lines(c(x1[i],x1[i]), c(x2[i-1], x2[i]), type="b", pch=19)
}
}
saveMovie(gibbs(), interval=0.1, moviename="",
movietype="gif", outdir=getwd(),
width=640, height=480)
この記事のまとめ
いかがでしたでしょうか?この記事では簡単な紹介程度しかできませんでしたが,ギブスサンプリングの動画などを見て少しでもイメージを掴んでもらえたら幸いです.今回は二変量正規分布からのギブスサンプリングを例に説明しましたが,MCMCは多変量でより力を発揮する手法ですし,複雑な確率分布からのサンプリングにも非常に有効です.この記事を読んで興味を持たれた方は,以下に挙げている参考資料などで読んで頂ければと思います.
参考資料
- 「パターン認識と機械学習 下巻」
- この記事のネタ本であり,機械学習系のバイブル.MCMCはかなり後の方に書かれているので,辿り着く人が少ないかもしれません....
- 「Rによるモンテカルロ法入門」
- 私は最初この本で勉強しました.ギブスサンプリングなどのMCMCはもちろんのこと,基礎となる乱数生成やモンテカルロ法も幅広く紹介されています.Rのコードが多数掲載されているので,実際に手を動かしながら勉強できるのも非常に良いです.そのかわり,MCMCがどういう状況でどう役に立つのかといったストーリー的な部分はあまり書かれていません.
- 読書ノートをBlogに書いています:http://yagays.github.com/blog/2012/10/20/archive-introducing-monte-carlo-methods-with-r/
- 「計算統計 2 マルコフ連鎖モンテカルロ法とその周辺」
- 「Rによるモンテカルロ法入門」であまり触れられていなかったMCMCの概説なら本書が一番分かりやすいと思います.なぜMCMCを使うのかといった話から,次元の呪いや詳細釣り合いなどの厳密な証明までひと通り網羅されていて,とりあえずこれを読めば大丈夫という感じ.
最後に
主催者であるnaoya_tさん,ならびにAdvent Calendar 2012の場を提供して頂いたQiitaの開発チームの皆様,ありがとうございました.
明日12/3の担当はniamさんです.よろしくお願いします!