はじめに
最近高校物理の復習をしていて、折角だからグラフを描く問題をmatplotlibで解いてみようと思ったんですが、一次関数のxの値で傾きが変わるやつを描くいいやり方がわからない。通る点をハードコーディングしてplt.plotに渡すという方法はすぐ見つかりましたが、できれば関数は関数として記述したい。しかし調べようと思っても「一次関数のxの値で傾きが変わるやつ」の呼び方がわからないから全然正解にたどり着けない。
といった具合に暗中模索していたんですが、小一時間かかってようやく「区分関数」という名称がわかり、numpy.piecewiseというソリューションに行き着くことができました。
私のように「区分関数」なんて言葉を知らない新米文系エンジニアのためにも、記事として残しておこうと思います。
やりたいこと
0 ≦ x ≦ 5 の範囲で、以下の区分関数のグラフを書きたい(xは0.1刻みとする)。
y = \begin{cases}
3x + 4 \quad(x ≦ 2) \\
10\hspace{29pt}(2 < x) \\
\end{cases}
numpy.piecewise(x, condlist, funclist)
区分関数(piecewise-defined function)を評価する関数。
x: 定義域。ドキュメントにはndarrayかscalarと書いてありますが、どんな時にscalarを使うかはわかりません。普通はarangeとかlinspaceで生成したndarrayを渡すんだと思います。
condlist: 条件文のリスト
funclist: 各条件文がTrueの時の関数のリスト
戻り値: xがndarrayの場合、xの各要素に指定の関数を適用したndarrayが返る。
コード
何も指定しないとy軸が切片の4からになってしまうので、原点を表示させるためにylimで表示範囲を指定しています。
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 5, 0.1)
y = np.piecewise(x, [x <= 2, x > 2], [lambda x: x * 3 + 4, 10])
plt.plot(x, y)
plt.ylim(0, 12)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
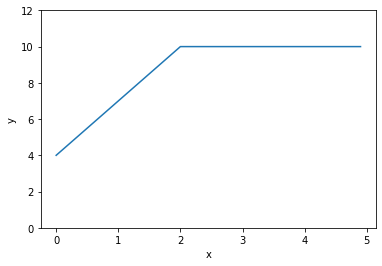
実行結果
Colaboratoryで実行し、想定通りのグラフが表示されました。
感想
やっぱり関数は関数のまま記述できたほうがすっきりしますね。
matplotlib初心者ですが、こんなところで躓くとは思っていませんでした。心が折れる前に解法が見つかってよかったです。
最後までご覧いただきありがとうございました。