PyMCでコインの確率推定

前回の続き見たいなもの。
PyMC3で同じようなことをやってみる。

PyMC

PyMCとはPythonのMCMCライブラリの一種。他にはpystan,emceeなどがあるが、現在主流なのはpystanとPyMC。速度はpystan > PyMCだけど、PyMCは離散変数のモデルの計算ができ、Pythonicな方法でモデルを記述できるのでpythonに慣れた人からすれば学習コストは比較的低い。
PyMCには、PyMC2系列とPyMC3系列があり、両者の間にはモデルの記述法など若干の違いがあり、PyMC3の方が高速。

確率分布

使用できる確率分布は公式ドキュメントを参照
https://pymc-devs.github.io/pymc/distributions.html

サンプリング方法

dir(pymc3.step_methods)で確認
NormalProposal,HamiltonianMC,Metropolis,,NUTSなど、有名所は揃ってる

実行環境

実行環境はlinux mint 64bitにanacondaを入れたものを使用した。
anacondaのデフォルトではpymc2が入っているので、以下のコマンドによってpymc3をインストール

pip install --process-dependency-links git+https://github.com/pymc-devs/pymc3

プログラム概要

with pm.Model()内部にモデルを記述。
事前分布やら尤度、サンプリング方法を定義して、
sample関数でサンプリングスタート。
traceplotに使うと簡単に実行結果を描画できる。

#coding:utf-8
import pymc3 as pm
import matplotlib.pyplot as plt
import numpy as np

observed = [1, 0, 1, 1, 0, 1, 0, 1, 0, 0]
h = sum(observed)
n = len(observed)
alpha, beta = 1, 1
niter = 10 ** 6
with pm.Model() as model:
    # define priors
    p = pm.Beta('p', alpha=alpha, beta=beta)
    # define likelihood
    y = pm.Binomial('y', n=n, p=p, observed=h)
    # inference
    start = {'p': 0.5}
    step = pm.Metropolis()
    trace = pm.sample(niter, step, start)
pm.traceplot(trace)
plt.show()

N = 10000
p, bins = np.histogram(trace["p"], bins=N, density=True)
theta = np.linspace(np.min(bins), np.max(bins), N)
print "ML:" + str(h / float(n))
print "MCMC:" + str(np.dot(p, theta) / N)

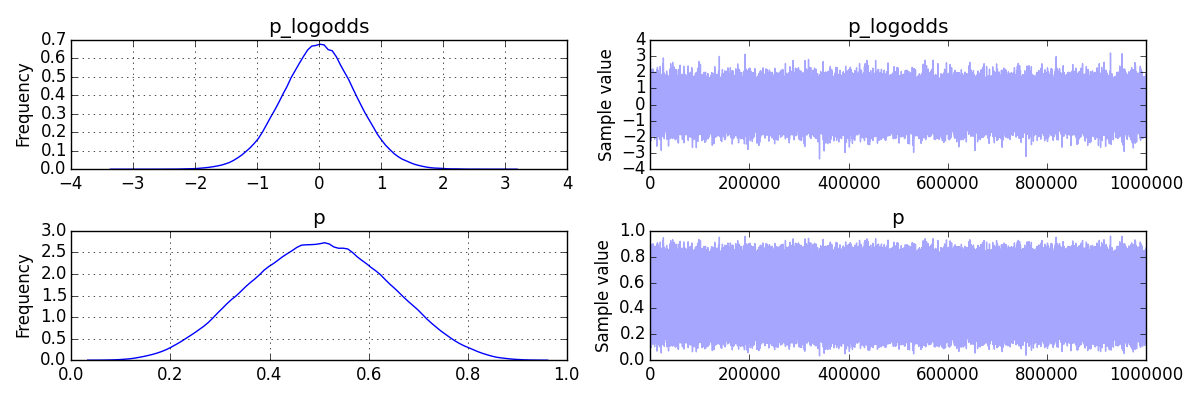
実行結果

事後分布の期待値は0.539。最尤推定による推定値は0.5であるのに対し、無視できない大きさ。
前回に推定したグラフと大体一致しているので、分布自体はそんなに間違っていないはず。
期待値の求め方間違っているような気がする。間違ってたら教えて下さい。

終わりに

ライブラリを使って、コインの表の出る確率を計算してみた。
次はもうちょっと複雑なデータとモデルを使って推定してみたい。

参考文献

岩波データサイエンス Vol 1
https://pymc-devs.github.io/pymc3/getting_started/
http://people.duke.edu/~ccc14/sta-663/PyMC3.html