MCMCを使ってコインの表が出る確率を推定する

概要

MCMCの勉強用。一番簡単な例としてベルヌーイ過程におけるパラメータの事後分布をMCMC及びベータ分布を用いて求めてみました。

MCMC概要

ベイズ統計におけるMCMC(マルコフ連鎖モンテカルロ)法
は乱数を使って事後分布を求める手法。

事後分布はベイズの定理を使うと

事後分布 = (尤度*事前分布)/(データの得られる確率)

によって求める事ができる。
ここで問題になってくるのが、右辺の分母データの得られる確率データの得られる確率p(D)はパラメータ $\theta$を使って積分消去して求めることができる。
しかし、パラメータの次元数が多くなってくると何重もの多重積分をしなければならない。
静的なモンテカルロ法を用いて近似的な積分値を求めることもできるが、次元数が大きくなってくると精度が落ちてしまう。
そこで、データの得られる確率を計算することを諦めて、尤度と事前分布だけから事後分布を推定したものがMCMC。

MCMCによって、関数の値に比例したサンプルを得ることができる。
そこで、尤度 * 事前分布についてMCMCによってサンプリングして、積分値が1になるように正規化すると、それが事後分布になる。

今回は、勉強のために最も簡単な場合であるコインを何回か投げて得られたデータからコインの表の出る確率密度関数を求めます。

尤度

コインの表の出る確率を$\mu$として、
コイントスは独立試行で{0,1}集合Dを得られたとします。

$D={0,1,...,0,1}$

この時尤度は

$p(D|\mu)=\prod_{n} \mu^{x_{n}} (1-\mu)^{1-x_{n}}$

事前分布

事前分布はコインについて特に事前情報を持っていないので一様な値を取る
p($\mu$)=1とします。

事後分布

MCMCを使う

以下の手順に従って、所定の回数ループしてサンプリングを行う。

パラメータ $\mu$の初期値を選ぶ
$\mu$をランダムに微少量動かして $\mu_{new}$ を得る
動かした結果、(尤度*事前分布)が大きくなった場合、動かした値に $\mu$ を $\mu_{new}$ に更新→2.へ
(尤度*事前分布)が小さくなった場合、(P(D|$\mu_{new}$)P( $\mu_{new}$)/(P(D|$\mu$)P( $\mu$)の確率で $\mu$を更新→2.へ

得られたサンプルのヒストグラムを積分して1になるよう正規化して、事後分布を得る。

解析的に求める

今回のモデルはベルヌーイ過程なので、ベータ分布を事前分布に仮定すると、
ベータ分布のパラメータを更新するだけで、事後分布を得ることができる。

コインの表が出た回数をm、裏が出た回数をlとし、a,bを予め決めたパラメータとすると

$p(\mu|m,l,a,b) = beta(m+a,l+b) $

となる。
事前分布が無情報事前分布とする時はa=b=1とする

プログラム

pythonで書いてみました。anaconda入っていれば動くと思います。
読みやすさを重視したので全く速くありません。

# coding:utf-8
from scipy.stats import beta
import matplotlib.pyplot as plt
import numpy as np


def priorDistribution(mu):
    if 0 < mu < 1:
        return 1
    else:
        return 10 ** -9


def logLikelihood(mu, D):
    if 0 < mu < 1:
        return np.sum(D * np.log(mu) + (1 - D) * np.log(1 - mu))
    else:
        return -np.inf

np.random.seed(0)
sample = 0.5
sample_list = []
burnin_ratio = 0.1
N = 10
# make data
D = np.array([1, 0, 1, 1, 0, 1, 0, 1, 0, 0])
l = logLikelihood(sample, D) + np.log(priorDistribution(sample))
# Start MCMC
for i in range(10 ** 6):
    # make candidate sample
    sample_candidate = np.random.normal(sample, 10 ** -2)
    l_new = logLikelihood(sample_candidate, D) + \
        np.log(priorDistribution(sample_candidate))
    # decide accept
    if min(1, np.exp(l_new - l)) > np.random.random():
        sample = sample_candidate
        l = l_new
    sample_list.append(sample)
sample_list = np.array(sample_list)
sample_list = sample_list[int(burnin_ratio * N):]

# calc beta
x = np.linspace(0, 1, 1000)
y = beta.pdf(x, sum(D) + 1, N - sum(D) + 1)

plt.plot(x, y, linewidth=3)
plt.hist(sample_list, normed=True, bins=100)
plt.show()

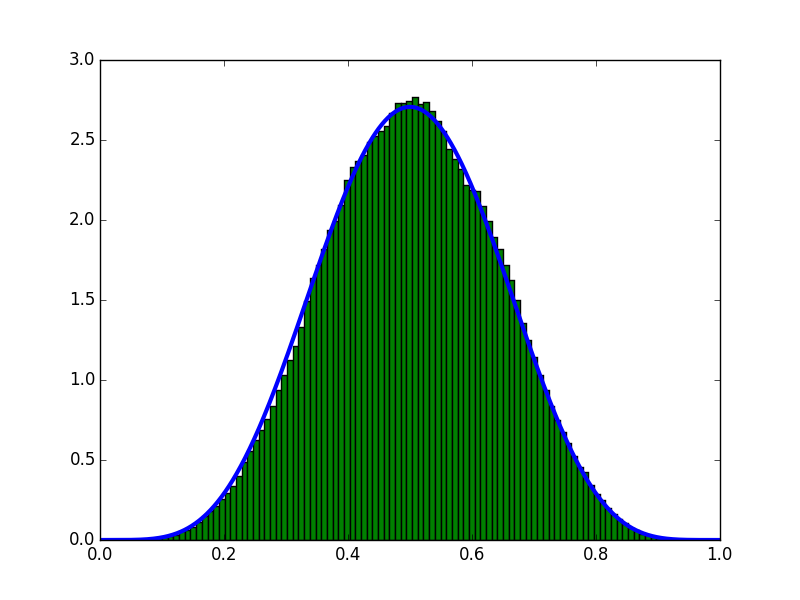
実行結果

サンプル数10回(表5回,裏5回)が得られたという条件で推定しました。
青い線が、解析的に求めたグラフ、ヒストグラムがMCMCで求めたグラフです。
グラフを見る限り、うまく推定できてることがわかります。

まとめ

今回はベルヌーイ分布のパラメータをpythonの手書きかつMCMCというとても非効率的な方法で求めました。
無情報事前分布かつ定義域が[0,1]の1変数というMCMCの恩恵を全く受ける事が出来ない問題設定でしたが、尤度(モデル)さえ定義できれば、後はパソコンに投げると事後分布を得られることが大分イメージできました。

実際にMCMCを使う場合は、StanやPyMCなどの最適化されたライブラリを使うのが吉でしょう。

事前分布やパラメータを変えて遊んでみると、観測データ数が大きくなるほど分布の幅が小さくなり事前分布の影響が少なくなるといったベイズ推定特有の性質を理解することができるかもしれません。

参考文献

データ解析のための統計モデリング入門
http://hosho.ees.hokudai.ac.jp/~kubo/stat/2013/ou3/kubostat2013ou3.pdf
http://tjo.hatenablog.com/entry/2014/02/08/173324