※ディスクレーマー:$O(n\log{n})$で問題ない場合も、たくさんあると思います。
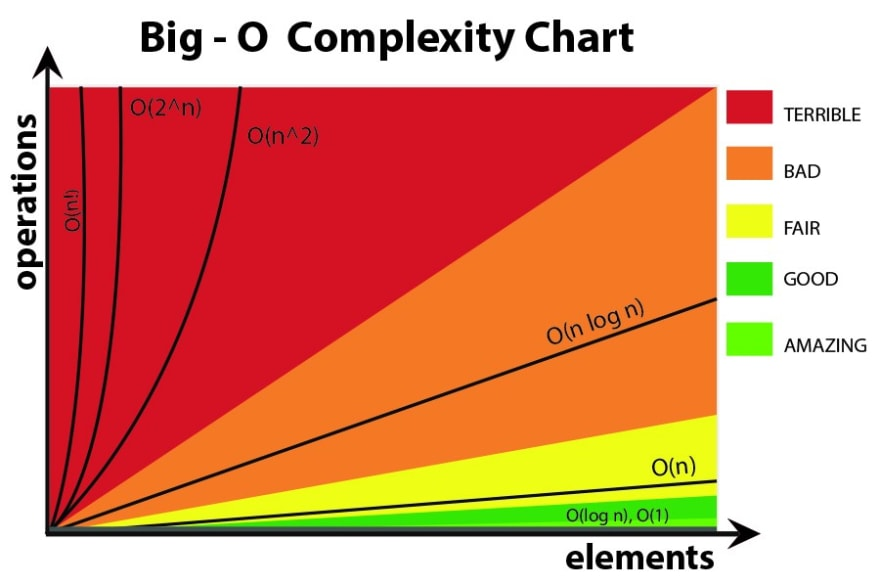
(↑計算量の一覧。画像元はこちら)
はじめに
素朴にソートすると$O(n\log{n})$な問題が、$O(n)$で求まるアルゴリズムについて解説する。
「パーティションベースの選択アルゴリズム」という。
例えば以下のような問題だ。
問題
数列からk 個の最大要素を求めよ。
(つまり、最大値~k番目に大きいものまでを求めよ)
※ただし、要素がソートされている必要はない
【例】
n=6, k=3
入力:[3,4,6,5,1,2]
出力:[4,6,5]
→上位3位までに入る数列を返す(ソートの必要なし)
解法0:素朴すぎる解法
大きい順のランキングを作ってから、k番目までを返す。
大きい順に並び変える際に、
- 1番大きいもの...
- 2番目に大きいもの...
- 3番目...
と探していく(「選択ソート」)
これにかかる計算量は$O(n^2)$である。これでは少し遅い。
解法1:素朴な解法
上のカイゼン。
大きい順のランキングを作ってから、k番目までを返す。
大きい順に並び変える際に、「マージソート」を利用する。
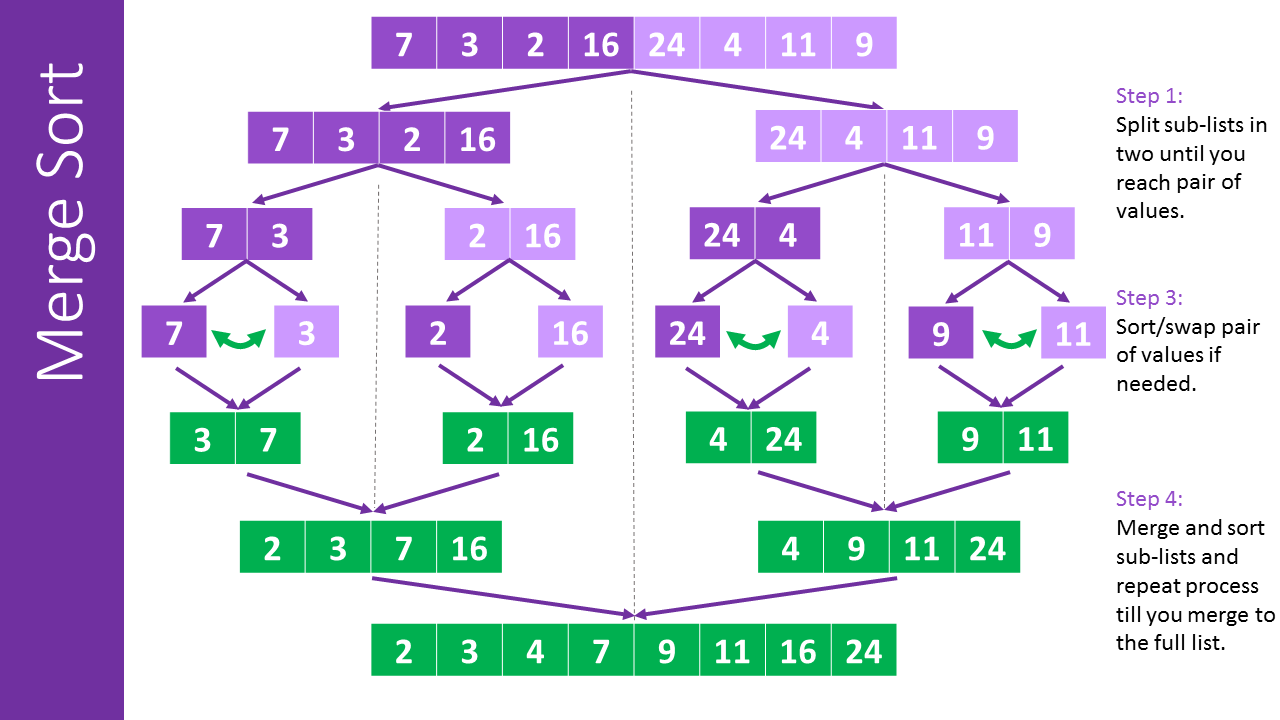
(↑マージソートのイメージ。画像元はこちら)
これにかかる計算量は$O(n\log{n})$である。
十分に思えるが、さらに早くするにはどうしたらいいか?
解法2:ちょっと早い解法
この解法に至るヒントは
「全てソートする必要はない(大きいk個が分かればいい)」
ということである
「優先度付きキュー」を利用する。
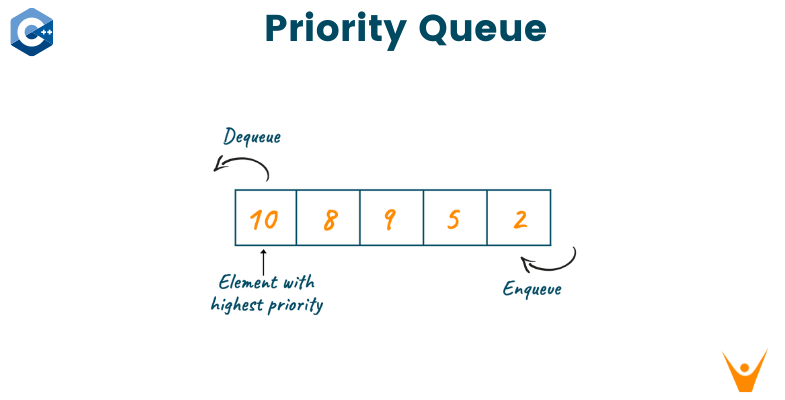
(↑優先度付きキューのイメージ。画像元はこちら)
まず、配列から適当なk個を優先度付きキューに入れる(この時点でk個をソートし、最小値が先頭になるようにする)
以下の操作を繰り返す。
元の配列の、残りの要素のうち1つを見て
- キューの最小値より小さければ何もしない
- 最小値より大きければ、キューの最小値を削除し、この要素をキューにソートして挿入
この挿入にはO(logk)かかる
操作の繰り返しは n 回程度発生するので、
全体にかかる計算量は$O(n\log{k})$である。
解法3:最適な解法
上の解法では、k個については並べ替えが発生してしまっており、$O(\log{k})$かかっている。
問題ではTOPが分かればいいのであって、TOPをランキング化する必要はない。
このランキング化をどうにか辞め、全体の計算量を$O(n)$にできないか考えたい。
そこで、「パーティションベースの選択アルゴリズム」の登場。
これは、「クイックソート」にかなり似ているアルゴリズムだ。
3-1. まず、一番左の値を基準(ピボット)として、左側に[その値未満の群]と[その値以上の群]に分かれるようにする
例えば冒頭の例では
基準:3(一番左の値)なので
[3,4,6,5,1,2]
を
[3未満の群]-[3以上の群]
に分解したい。その際に以下のような手順を踏む
3-2. 左端から見てピボット以上の値と、右端から見てピボット未満の値の場所を交換する
[3,4,6,5,1,2]
は
[3,4,6,5,1,2]
3と2、4と1が交換され
[2,1,6,5,4,3]
となる。群で言うと(2,1)-(6,5,4,3)になっているイメージだ。(3-1で述べたように左側に[その値未満の群]と[その値以上の群]に分かれるようになっている!)
3-3. この操作を再帰的に繰り返す。ただし、右からk番目までの要素が入っている群だけ繰り返せばよい
クイックソートでは
[2,1]
に対しても3-2と同じことをして
[1,2]とするのだが、このソートは必要ない。
なぜなら、冒頭の問題ではk=3であり、3番目までに大きいモノを返せばいいからだ。
右側の[6,5,4,3]の群が3個以上ある時点で、[2,1]の要素がトップ3に入ってくる可能性は
ゼロなのである。
したがって、
[6,5,4,3]についてだけ3-2と同じ操作を繰り返すと
今度は、基準:6(一番右の値)
なので、3と6が交換され
[3,5,4,6]
となる。群で言うと(2,1)-(3,5,4)-(6)になっているイメージだ。
真ん中の群について繰り返すと
[3,5,4]は[3,5,4]のままだ。この場合(3)-(5,4)に分解する。
3-4. 右から「ちょうど」k番目の要素まで分解出来たら、そこで終わり。
今回は(2,1)-(3)-(5,4)-(6)となっているので、[5,4,6]を返せばよい
まとめ
クイックソートに近いが、「パーティションベースの選択アルゴリズム」の場合「いらない場所はソートしない」と切り捨てることができるので、平均$O(n)$で計算することが可能なのだ!
参考
「選択アルゴリズム」と「中央値の中央値」
http://www.flint.jp/blog/?entry=109
中央値を線形時間で選択するアルゴリズムについて
https://techblog.nhn-techorus.com/archives/15289