本記事は ICLR2019をよむアドベントカレンダー Advent Calendar 2018 の12月9日分の記事です。
12月8日の担当はhiromuさんの論文紹介: Enabling Factorized Piano Music Modeling and Generation with the MAESTRO Datasetでした。
今回取り上げる論文は Quasi-hyperbolic momentum and Adam for deep learning です。
概要
- SGD, Momentum, Nesterovの加速勾配降下法, PID制御アルゴリズム等のパラメータ最適化手法を統一的な表現で内包するQHM(Quasi hyperbolic momentum)を提案
- Momentumアルゴリズムにおけるmomentum bufferと勾配の加重平均をもとにパラメータを更新
- 既存の最適化手法と比較して多くのタスクで学習時、バリデーション時でのメトリクス改善を実現
Open reviewということでAnonymousだが、arxivを見るとFacebook AI Researchから出た論文の模様。pytorchのレポジトリにはすでにPullRequestが上がっている。
Quasi hyperbolicは直訳すると準双曲だが、このアルゴリズムは行動経済学における双曲割引の理論(Laibson 1997)にインスパイアされている。
アルゴリズム
QHMでは直近割引因子(immediate discount factor) $\nu$ が導入され、以下のような更新規則をとる。
g_{t + 1} \leftarrow \beta \cdot g_t + (1 - \beta) \cdot \nabla \hat{L}_t (\theta_t)
\theta_{t + 1} \leftarrow \theta_t - \alpha [ (1 - \nu) \cdot \nabla \hat{L}_t (\theta_t) + \nu \cdot g_{t+1} ]
$g_t$ は momentum buffer とよばれ、この式で $\nu = 1$ とすればMomentumアルゴリズムの更新規則
g_{t + 1} \leftarrow \beta \cdot g_t + (1 - \beta) \cdot \nabla \hat{L}_t (\theta_t)
\theta_{t + 1} \leftarrow \theta_t - \alpha \cdot g_{t + 1}
がえられ、$\nu = 0$ とすればSGDの更新規則
\theta_{t + 1} \leftarrow \theta_t - \alpha \cdot \nabla \hat{L}_t (\theta_t)
がえられる。
Momentumアルゴリズムの更新規則とQHMの更新規則は似ているように思え、前者のハイパーパラメータをいじれば後者を再現できそうに見えるが、再現できないことは解析的に示される。
Momentumアルゴリズムでは $\beta$ を増加させることで momentum buffer のばらつきは抑えられるが、同時に momentum buffer が使い物にならないほど劣化してしまう。QHMではこの劣化を、直近の勾配分の重みを加えることで緩和しようとしている。
他アルゴリズムとの関連
QHMは他の最適化手法アルゴリズムと次のような関連性がある。
QHMは既存のアルゴリズムを内包しており、最近提案された最適化手法も内包している。ただし、RechtのPIDアルゴリズムについてはQHMを内包している。
単一のmomentum buffer以外にも複数のmomentum bufferを使ったアルゴリズムAggmo(Lucas et al., 2018) があり、これもQHMを内包している。
QHAdam
Adamアルゴリズム(Kingma & Ba, 2015)に対応して、パラメータの更新の際にmomentum bufferと勾配、勾配自乗との加重平均をとることでQHAdamというアルゴリズムを提案した。
g_{t + 1} \leftarrow \beta_1 \cdot g_t + (1 - \beta_1) \cdot \nabla \hat{L}_t (\theta_t)
g^\prime_{t +1} \leftarrow \frac {1} {1 - \beta^{t+1}_1} \cdot g_{t + 1}
s_{t + 1} \leftarrow \beta_2 \cdot s_t + (1 - \beta_2)(\nabla \hat{L}_t (\theta_t))^2
s^\prime_{t + 1} \leftarrow \frac{1}{1 - \beta^{t + 1}_2} \cdot s_{t + 1}
\theta_{t + 1} \leftarrow \theta_t - \alpha \Bigg[ \frac{(1 - \nu_1) \cdot \nabla \hat{L}_t (\theta_t) + \nu_1 \cdot g^\prime_{t+1}}{\sqrt{(1 - \nu_2)(\nabla \hat{L}_t (\theta_t))^2 + \nu_2 \cdot s^\prime_{t+1}} + \epsilon} \Bigg]
この式で $\nu_1 = 1, \nu_2 = 1$ とすることでAdamの更新規則を得られる。また、下記のパラメータを取ることで既存の以下のアルゴリズムを得られる。
- $\nu_1 = 0, \nu_2 = 1$ : RMSProp
- $\nu_1 = \beta_1, \nu_2 = 1$ : NAdam (Dozat, 2016)
QHAdamにおける $\nu_1, \beta_1$ はQHMの $\nu, \beta$ と同様な意味を持つ。
AdamをQHAdamに置き換える時は、Adamの訓練が順調な場合は $\nu_2 = 1$ とし $\beta_2$ を変更しないことでうまくいく。もしもAdamの訓練が順調でない場合は、$\nu_2 < 1$ とすると学習の安定性が増す。
実験
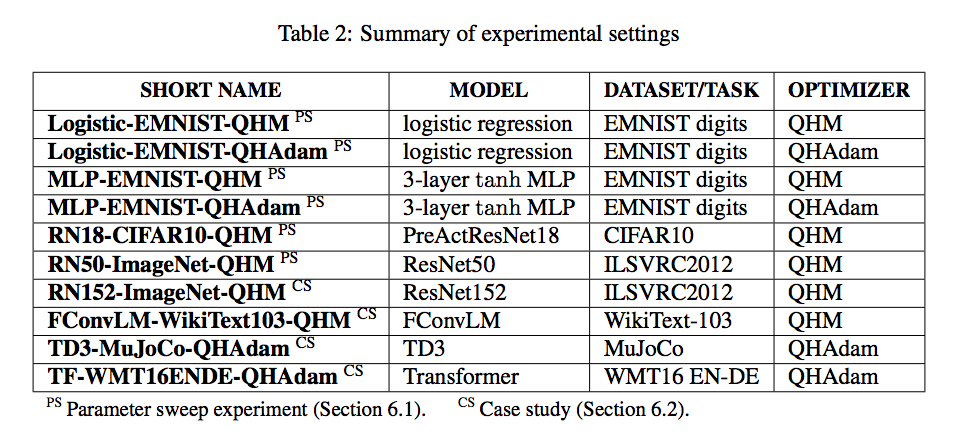
下記のモデル、タスク/データセット、最適化アルゴリズムで実験を行った。
モデル、タスク/データセットについて下三段は次を表す。
-
FConvLM: Gated Convolutional Network(Dauphin et al., 2016)を用いた言語モデル
-
TD3: Actor Criticアーキテクチャ(Fujimoto et al., 2018)による強化学習モデル
-
Transformer: 機械翻訳モデル(Vaswani et al., 2017)
-
MuJoCo: ロボットシミュレーション向けの物理エンジン構築タスク
-
WMT16 EN-DE: 英語→ドイツ語翻訳データセット
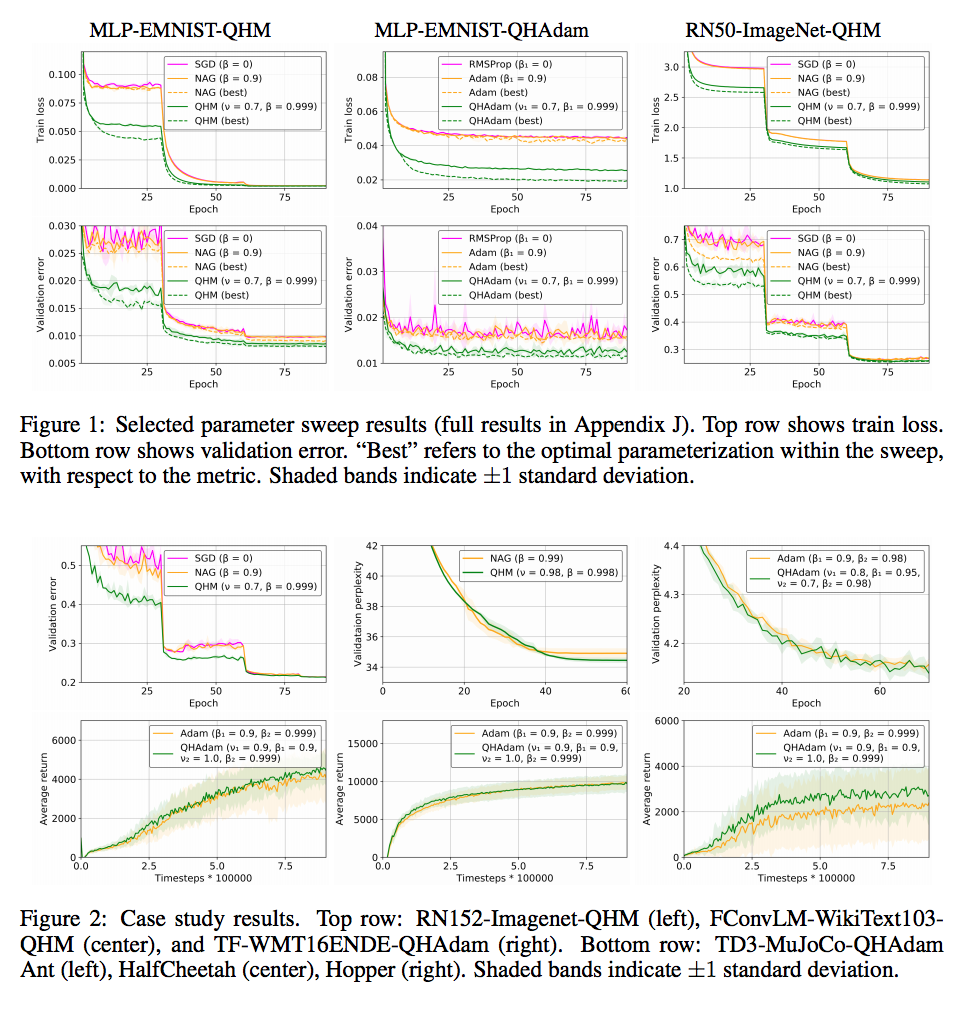
以下は結果の一部。MLP, ResNet系のタスクで学習データロス、バリデーションエラー共に良好な結果を得ている。
ハイパーパラメータチューニングについて
QHMについては経験則上 $\nu = 0.7, \beta = 0.999$ が良好だった。
QHAdamについては場合によるが、Adamで安定していたタスクについては $\nu_2 = 1$, $\beta_2$ を変更なしにすると良好な結果が得られた。
Momentumアルゴリズム/Nesterov加速勾配降下法をQHMで置き換える時には学習率の違いに注意する。前者での学習率 $\alpha$ と momentum bufferの更新ファクタ $\beta$ を用いてQHMでの学習率は $\alpha \cdot (1 - \beta)^{-1}$ と表せる。
感想
今回論文系のAdvent Calendarは初参加でした。この論文を選んだ理由としては恐縮ですが、OpenReviewの中からコメント数の多いもので、かつ実装が公開されているからという単純なものでした。
最初なんでQuasi-hyperbolicというタイトルなんだろうとクエスチョンマークをつけながら読み進めていました。読み込むにつれて、行動経済学の双曲割引という概念とリンクしていることがAppendix等で明らかになり、割合面白かったです(小並感
本論文のAppendixでは双曲割引からどのような過程を経てQHMにたどりついたかや、Adam安定性の議論、並びに複数のmomentum bufferを持つAggMoアルゴリズムとの関連が語られますが、全部を読めていないため、解説は省きます。気が向いたらAppendixに関連したPostをするかもしれません。