MDR社のblueqatのチュートリアルを読み終えたので、備忘録として巡回セールスマン問題を解いていきたいと思います。
blueqatのチュートリアルはこちらからどうぞ。
巡回セールスマン問題とは
巡回セールスマン問題とは、「与えられた地点を全てまわる順番を、その地点間の距離(コスト)をもとに最適化する。」 問題です。
例題を示します。
以下の様な都市A,B,C,Dがあった時に、全ての地点を最も効率よく回る順番を決めていきます。
各エッジに書いてある数値は各地点間の距離を示しています。
(今回は簡単にするために完全グラフにしていますが、完全グラフでなくても大丈夫です。)
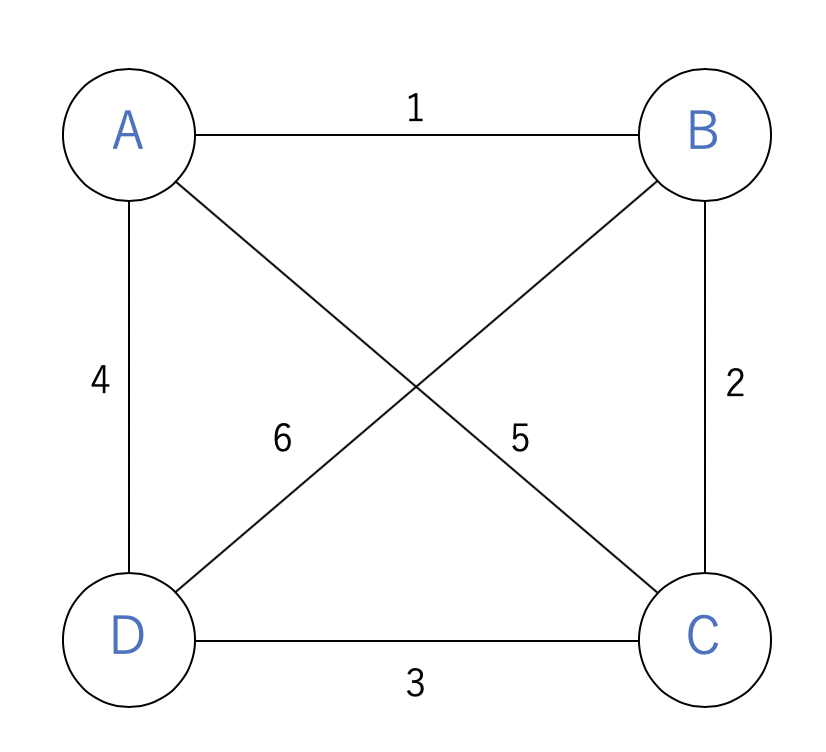
この問題を考えると、
A →(+1)→ B →(+2)→ C →(+3)→ D →(+4)→ A
と回るのが最も効率がいいのがわかります。
実際、このルートだと、 $1+2+3+4=10$と最も距離を最小に抑えられています。
また巡回セールスマン問題は、NP困難に分類されます。
P,NP,NP困難の分類に関しては、こちらがわかりやすかったです。
目的関数
アニーリングをする際に最も考えなければいけないことは、目的関数(ハミルトニアン)の設定です。
アニーリングの目的は、この目的関数の最小解を求めることにあります。
またここで、目的関数 $H$とは「問題の解として適しているかどうか」を判別するものになります。
ではここで、今回の目的関数をみていきましょう。
H = \sum_{v=1}^N\left( 1-\sum_{j=1}^N x_{v,j} \right)^2 + \sum_{j=1}^N\left(1-\sum_{v=1}^Nx_{v,j} \right)^2 + B\sum_{(u,v)\in E}W_{u,v}\sum_{j=1}^N x_{u,j} x_{v,j+1}
x_{v, j} =
\left\{
\begin{array}{ll}
1 & (都市vにj番目に訪れる) \\
0 & (都市vにj番目に訪れない)
\end{array}
\right.\\
B = 重み(ハイパーパラメータ)\\
W_{u, v} = u,v間の距離 \\
N = 都市の数
上の様になります。
また、ここで出てきた $x_{v, j}$についてQUBOマトリクスに変形させます。
QUBOマトリクス
QUBOマトリクスとは、アニーリングするために必要な目的関数を上三角行列に変形させたものになります。
また、QUBOマトリクスは2次元でしか表せないので、今回の $x_{v, j}$も強引に2次元に表してみます。
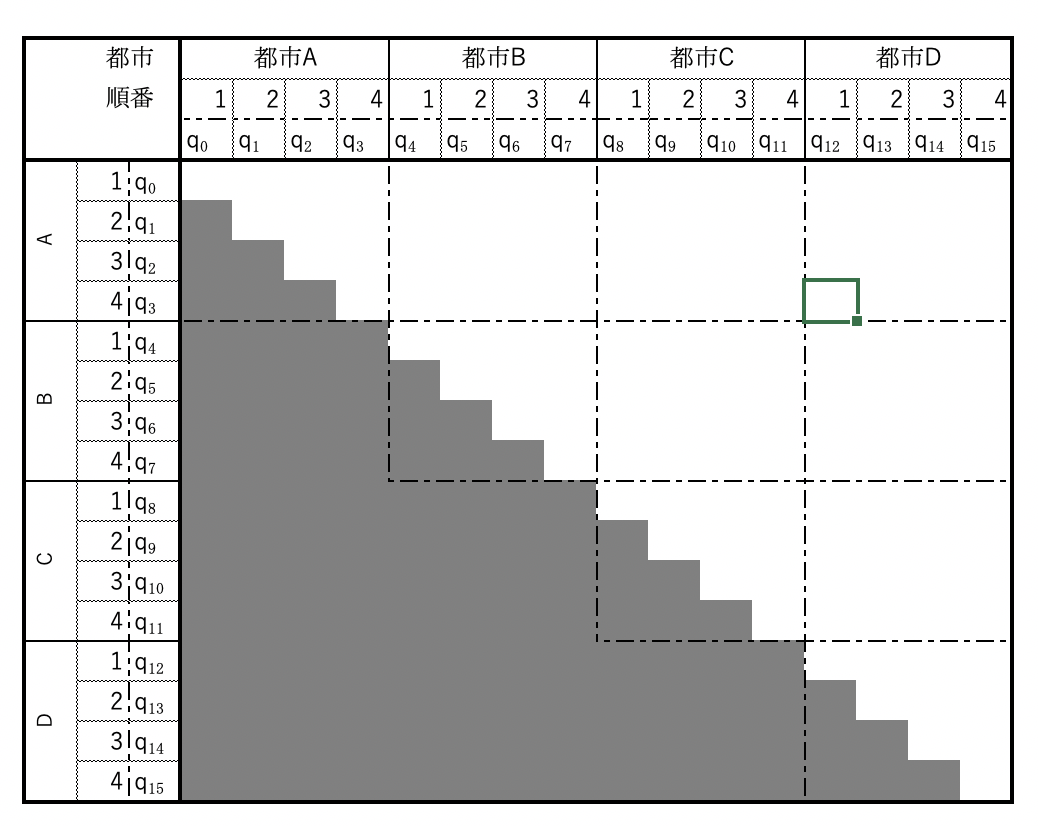
例えば、この時の$q_0$は「都市Aを1番目に訪れる」ことを表します。
以降はこの$q$の係数を変化させていくことで、アニーリングをしていきます。
では少し脱線しましたが、目的関数のそれぞれの項が何を示しているか確認していきましょう。
第1項:各都市は1回しか訪れてはいけない
\sum_{v=1}^N\left( 1-\sum_{j=1}^N x_{v,j} \right)^2
巡回セールスマン問題では、各都市は必ず1回は訪れなければいけないものの2回以上は訪れてはいけません。
そのため例題の答えでいうと、
| v\j | 1番目 | 2番目 | 3番目 | 4番目 | = | 第1項 |
|---|---|---|---|---|---|---|
| A | 1 | 0 | 0 | 0 | {1-(1+0+0+0)}^2 | |
| B | 0 | 1 | 0 | 0 | {1-(0+1+0+0)}^2 | |
| C | 0 | 0 | 1 | 0 | {1-(0+0+1+0)}^2 | |
| D | 0 | 0 | 0 | 1 | {1-(0+0+0+1)}^2 | |
| 合計 | 0 | |||||
| となり、第1項が最小になっていることがわかります。 |
またこれを一般的な形に直すと、
| v\j | 1番目 | 2番目 | 3番目 | 4番目 | = | 第1項 |
|---|---|---|---|---|---|---|
| A | $q_0$ | $q_1$ | $q_2$ | $q_3$ | $(1-(q_0+q_1+q_2+q_{3}))^2$ | |
| B | $q_4$ | $q_5$ | $q_6$ | $q_{7}$ | $(1-(q_4+q_5+q_6+q_{7}))^2$ | |
| C | $q_8$ | $q_9$ | $q_{10}$ | $q_{11}$ | $(1-(q_8+q_9+q_{10}+q_{11}))^2$ | |
| D | $q_{12}$ | $q_{13}$ | $q_{14}$ | $q_{15}$ | $(1-(q_{12}+q_{13}+q_{14}+q_{15}))^2$ | |
| となるため、これらの総和を求めると |
$
{(1-q_0-q_1-q_2-q_3)^2+(1-q_4-q_5-q_6-q_7)^2+(1-q_8-q_9-q_{10}-q_{11})^2+(1-q_{12}-q_{13}-q_{14}-q_{15})^2
}
$
第2項:同じタイミングに複数の都市に行くことはできない
\sum_{j=1}^N\left(1-\sum_{v=1}^Nx_{v,j} \right)^2
巡回セールスマン問題では、当たり前の様に同じタイミングに複数の都市に訪れることを許していません。
そのため、第1項と同じ様に考えると、
| j\v | A | B | C | D | = | 第2項 |
|---|---|---|---|---|---|---|
| 1番目 | 1 | 0 | 0 | 0 | $(1-(1+0+0+0))^2$ | |
| 2番目 | 0 | 1 | 0 | 0 | $(1-(0+1+0+0))^2$ | |
| 3番目 | 0 | 0 | 1 | 0 | $(1-(0+0+1+0))^2$ | |
| 4番目 | 0 | 0 | 0 | 1 | $(1-(0+0+0+1))^2$ | |
| 合計 | 0 | |||||
| という様な表が描けます。 |
| j\v | A | B | C | D | = | 第2項 |
|---|---|---|---|---|---|---|
| 1番目 | $q_0$ | $q_4$ | $q_8$ | $q_{12}$ | $(1-(q_0+q_4+q_8+q_{12}))^2$ | |
| 2番目 | $q_1$ | $q_5$ | $q_9$ | $q_{13}$ | $(1-(q_1+q_5+q_9+q_{13}))^2$ | |
| 3番目 | $q_2$ | $q_6$ | $q_{10}$ | $q_{14}$ | $(1-(q_2+q_6+q_{10}+q_{14}))^2$ | |
| 4番目 | $q_3$ | $q_7$ | $q_{11}$ | $q_{15}$ | $(1-(q_3+q_7+q_{11}+q_{15}))^2$ | |
| となるため、これらの総和を求めると |
${(1-q_0-q_4-q_8-q_{12})^2+(1-q_1-q_5-q_9-q_{13})^2+(1-q_2-q_6-q_{10}-q_{14})^2+(1-q_{3}-q_{7}-q_{11}-q_{15})^2
}$
となる。
これを、第1項とまとめて展開してみると
${2q_0q_1 + 2q_0q_{12} + 2q_0q_2 + 2q_0q_3 + 2q_0q_4 + 2q_0q_8 - 2q_0}$
${+ 2q_1q_{13} + 2q_1q_2 + 2q_1q_3 + 2q_1q_5 + 2q_1q_9 - 2q_1}$
${ + 2q_{10}q_{11} + 2q_{10}q_{14} + 2q_{10}q_2 + 2q_{10}q_6 + 2q_{10}q_8 + 2q_{10}q_9 - 2q_{10} }$
${+ 2q_{11}q_{15} + 2q_{11}q_3 + 2q_{11}q_7 + 2q_{11}q_8 + 2q_{11}q_9 - 2q_{11}}$
${+ 2q_{12}q_{13} + 2q_{12}q_{14} + 2q_{12}q_{15} + 2q_{12}q_4 + 2q_{12}q_8 - 2q_{12} }$
${+ 2q_{13}q_{14}+ 2q_{13}q_{15} + 2q_{13}q_5 + 2q_{13}q_9 - 2q_{13} }$
${+ 2q_{14}q_{15} + 2q_{14}q_2 + 2q_{14}q_6 - 2q_{14}}$
${+ 2q_{15}q_3 + 2q_{15}q_7 - 2q_{15}}$
${+ 2q_2q_3 + 2q_2q_6 - 2q_2 + 2q_3q_7 - 2q_3 }$
${+ 2q_4q_5 + 2q_4q_6 + 2q_4q_7 + 2q_4q_8 - 2q_4 + 2q_5q_6 + 2q_5q_7 + 2q_5q_9 - 2q_5 }$
${ +2q_6q_7 - 2q_6 - 2q_7 + 2q_8q_9 - 2q_8 - 2q_9 + 8}$
となる。
またこれをQUBOマトリクスにそれぞれの係数を描きだしてみると
 このようになります。
このようになります。
また、第1項と第2項のような制約を表す関数をペナルティー関数と言います。
第3項:各都市間の距離を加味する
B\sum_{(u,v)\in E}W_{u,v}\sum_{j=1}^N x_{u,j} x_{v,j+1}
この項では、「都市$u$に$j$番目に訪れた後に、都市$v$に$j+1$番目に訪れる」ことについて考えています。
わかりやすくいうと、
x_{u, j}x_{v, j+1} =
\left\{
\begin{array}{ll}
1 & (都市uにj番目に訪れたのちに、都市vにj+1番目に訪れる) \\
0 & (それ以外)
\end{array}
\right.\\
$x_{u, j}x_{v, j+1} = 1$の時は、$u,v$間の距離 $W_{u,v}$をかけます。
また、先ほど述べた様に $B$はハイパーパラメータなので自分で設定する必要があります。
これも今回の例題を用いて、QUBO関数に落とし込んでみましょう。
 このとき、見易くするために$B$を無視して考えています。
このとき、見易くするために$B$を無視して考えています。
また、第3項のような問題特有の重みをかける関数をコスト関数と言います。
総和
以上で各項のQUBOが出揃ったので第3項に$B$をかけることに注意して、今回の目的関数全体のQUBOを計算すると、

となります。
あとはこれをアニーリングマシンにぶち込めば出てくるので、実際に試してみましょう。
実装
では以上で出たQUBOをPythonで実現してみましょう。
必要なモジュールは以下の2つです。
import blueqat.opt as wq
import numpy as np
入力セル
print("Number of cities:")
pu_cities_size = int(input())
print("The cost of constraint:")
pu_B = float(input())
cost_matrix = np.array([[0,1,1],[0,2,5],[0,3,4],[1,0,1],[1,2,2],[1,3,6],[2,0,5],[2,1,2],[2,3,3],[3,0,4],[3,1,6],[3,2,3]])
pu_cities_sizeは都市の数、
pu_Bはハイパーパラメータである$B$の値です。
また今回は各都市間の距離、結びつきをcost_matrixとして記述しています。
ペナルティー関数:第1項 + 第2項
ペナルティー関数である第1項と第2項は本質は一緒なので、まとめて計算することができます。
def get_traveling_qubo(cities_size):
qubo_size = cities_size*cities_size
traveling_qubo = np.zeros((qubo_size, qubo_size))
indices = [(u, v, i, j) for u in range(cities_size) for v in range(cities_size) for i in range(cities_size) for j in range(cities_size)]
for u, v, i, j in indices:
ui = u * cities_size + i
vj = v * cities_size + j
if ui > vj:
continue
if ui == vj:
traveling_qubo[ui][vj] -= 2
if u == v and i != j:
traveling_qubo[ui][vj] += 2
if u < v and i == j:
traveling_qubo[ui][vj] += 2
return traveling_qubo, qubo_size, cities_size
traveling_qubo, qubo_size, cities_size = get_traveling_qubo(pu_cities_size)
コスト関数:第3項
cost_matrixを用いて、第3項を計算しています。
def get_traveling_cost_qubo(qubo_size, cities_size, cost_matrix):
traveling_cost_qubo = np.zeros((qubo_size, qubo_size))
indices = [(u, v, i, j) for u in range(cities_size) for v in range(cities_size) for i in range(cities_size) for j in range(cities_size)]
for u, v, i, j in indices:
ui = u * cities_size + i
vj = v * cities_size + j
k = abs(i - j)
if ui > vj:
continue
if (k ==1 or k == cities_size-1) and u < v:
for r in range(len(cost_matrix)):
if cost_matrix[r][0] == u and cost_matrix[r][1] == v:
traveling_cost_qubo[ui][vj] += cost_matrix[r][2]
return traveling_cost_qubo
traveling_cost_qubo = get_traveling_cost_qubo(qubo_size, cities_size, cost_matrix)
観測
実際に、目的関数のQUBOをアニーリングマシンに通して観測しています。
def get_travelingsalesman_qubo(traveling_cost_qubo, traveling_qubo, B):
a = wq.opt()
a.qubo = traveling_qubo + traveling_cost_qubo * B
answer = a.sa()
print(answer)
a.plot()
return answer
では今までの一連の流れを繋げてみましょう。
出力
traveling_qubo, qubo_size, cities_size = get_traveling_qubo(pu_cities_size)
traveling_cost_qubo = get_traveling_cost_qubo(qubo_size, cities_size, cost_matrix)
q = get_travelingsalesman_qubo(traveling_cost_qubo, traveling_qubo, pu_B)
[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]
 $B = 0.25$にすると、以上のようになりました。
出力の$[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]$は
$B = 0.25$にすると、以上のようになりました。
出力の$[1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1]$は
 という風にみることができます。
という風にみることができます。
一応これで、巡回セールスマン問題を解くことができました。
ここからは、この出力が本当に正しいかどうか目的関数(ハミルトニアン)を逆算していこうと思います。
目的関数の検証
def calculate_H_f(q, cities_size):
H_f = 0
for v in range(cities_size):
sum_x = 0
for i in range(cities_size):
index = v * cities_size + i
sum_x += q[index]
H_f += (1 - sum_x) ** 2
print(H_f)
return H_f
def calculate_H_s(q, cities_size):
H_s = 0
for i in range(cities_size):
sum_x = 0
for v in range(cities_size):
index = v * cities_size + i
sum_x += q[index]
H_s += (1 - sum_x) ** 2
print(H_s)
return H_s
def calculate_H_t(q, cities_size, cost_matrix):
H_t = 0
indices = [(u, v, i, j) for u in range(cities_size) for v in range(cities_size) for i in range(cities_size) for j in range(cities_size)]
for u, v, i, j in indices:
ui = u * cities_size + i
vj = v * cities_size + j
k = abs(i - j)
if ui >= vj:
continue
if k == 1:
if q[ui] == 1 and q[vj] == 1:
for k in range(len(cost_matrix)):
if cost_matrix[k][0] == u and cost_matrix[k][1] == v:
H_t += cost_matrix[k][2]
print(H_t)
return H_t
def calculate_H(q, cities_size, cost_matrix, B):
print("hamiltonian_f =")
H_f = calculate_H_f(q, cities_size)
print("hamiltonian_s =")
H_s = calculate_H_s(q, cities_size)
print("hamiltonian_t =")
H_t = calculate_H_t(q, cities_size, cost_matrix)
H = H_f + H_s + H_t * B
print("hamiltonian =")
print(H)
return H
calculate_H(q, cities_size, cost_matrix, pu_B)
これによって、出力からその目的関数の値を調べることができます。
ではこれを加味した上で出力してみましょう。
traveling_qubo, qubo_size, cities_size = get_traveling_qubo(pu_cities_size)
traveling_cost_qubo = get_traveling_cost_qubo(qubo_size, cities_size, cost_matrix)
for i in range(10):
q = get_travelingsalesman_qubo(traveling_cost_qubo, traveling_qubo, pu_B)
calculate_H(q, cities_size, cost_matrix, pu_B)
おそらくhamiltonianの値が $2.25, 2.0, 1.75, 1.5$の4パターン出てきたのではないでしょうか?
これは最後の1回を含めていないため生じています。
この最後の一回とは例題でいう、
A →(+1)→ B →(+2)→ C →(+3)→ D (→(+4)→ A)
この太字の部分になります。
そのため、往復の最短経路ではなく往路のみの最短経路が知りたい場合は、この中でも最小の目的関数の値である$1.5$の経路を採択すればいいことがわかります。
以上で、巡回セールスマン問題を解いてみました。
まとめ
今回はblueqatを用いて、巡回セールスマン問題を解くことができました。
次回は、交通最適化を実装してみたいと思います。