[第6章]に引き続き、深層学習(青イルカ本)の第7章を読み進めていく。
本章の概要
これまではサンプルの次元が固定のニューラルネットを扱ってきた。
しかし本章では、系列データの分類問題を扱う。
系列データとは、個々の要素が順序付きの集まりとして与えられたものであり、サンプルごとに系列の長さが異なる。
こうした系列データを扱うために以下のネットワークを使っていく。
- Recurrent Neural Network(RNN)
- 系列長が異なるサンプルの予測・学習
- Long Short-Term Memory(LSTM)
- 系列長が非常に大きいデータの予測
RNN
RNNとは?
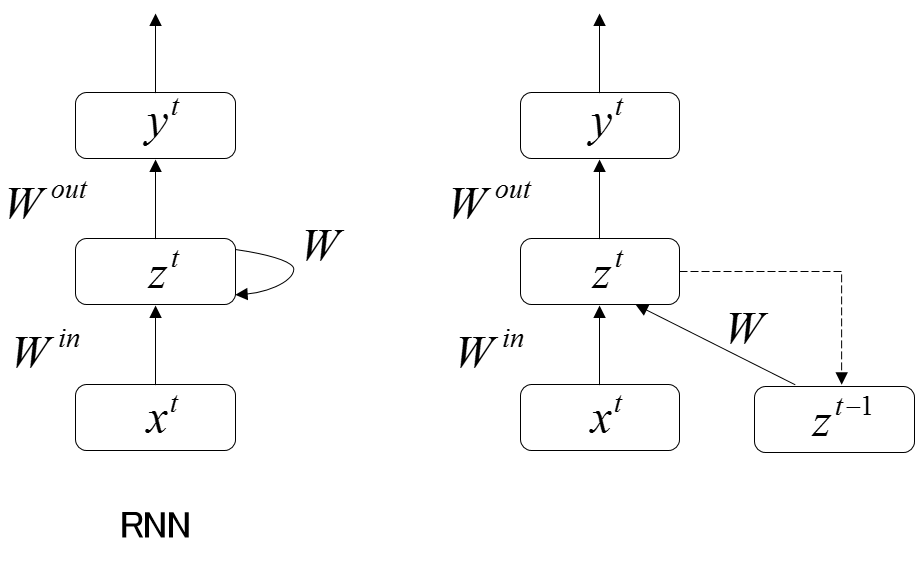
内部に閉路を持つニューラルネットの総称。
RNNは、過去のすべての入力から1つの出力への写像を表現する。
入出力定義
- 入力層ユニット
- 入力 $\boldsymbol{x^t} = (x_i^t)$
- 中間層ユニット
- 入力 $\boldsymbol{u^t} = (u_j^t)$
- 出力 $\boldsymbol{z^t} = (z_j^t)$
- 出力層ユニット
- 入力 $\boldsymbol{v^t} = (v_j^t)$
- 出力 $\boldsymbol{y^t} = (y_j^t)$
重み定義
- 入力層と中間層間の重み $\boldsymbol{W^{(in)}} = (w_{ji}^{(in)})$
- 中間層から中間層への帰還路の重み $\boldsymbol{W} = (w_{jj^{\prime}})$
- 中間層と出力層間の重み $\boldsymbol{W^{(out)}} = (w_{kj}^{(out)})$
RNNの順伝播計算は?
中間層の入力
時刻 $t$ における中間層の各ユニットへの入力は、
$t$ に入力層から伝達されるもの + 時刻 $t-1$ の中間層の出力、となる。
$$
u_j^t = \sum_{i} w_{ji}^{(in)} x_i^t + \sum_{j^{\prime}} w_{jj^{\prime}} z_{j^{\prime}}^{t-1}
$$
中間層の出力
中間層の出力は、活性化関数 $f$ を施したものとなる。
$$
z_j^t = f(u_j^t)
$$
よって、
$$
\boldsymbol{z_t} = \boldsymbol{f}(\boldsymbol{W}^{(in)} \boldsymbol{x}^t + \boldsymbol{W} \boldsymbol{z}^{t-1})
$$
ネットワークの出力
$$
\boldsymbol{y_t} = \boldsymbol{f^{(out)}}(\boldsymbol{v})^{t} = \boldsymbol{f^{(out)}}(\boldsymbol{W}^{(out)} \boldsymbol{z}^{t})
$$
RNNの逆伝播計算は?
BTRL法とBPTT法がある。
- BTRL法
- realtime recurrent learning
- メモリ効率が良い
- BPTT法
- backpropagation through time
- 計算が高速
- シンプル
簡単なので省略.
RNNで勾配が不安定になるのはなぜ?
RNNは系列データの入力履歴の長さに応じて、層が深くなる。
層が深くなると、誤差逆伝播法により勾配を計算するとき、層を遡るにつれて勾配が消失するか爆発してしまう性質がある。
RNNでは短期的な記憶は実現できても、より長期にわたる記憶を実現するのは難しいと表現することもできる。
LSTM
わかるLSTMを参照すると,本当にわかる.
このスライドも大変参考になる.
CTC(Connectionist Temporal Classification)
入力と出力の系列長が異なるときに用いられる。
任意のRNNやLSTM等の出力に適用できる。
出力に何も出力しなことを示す空白を導入し、許容することで系列長の違いを吸収する。
これにより単語数や音素数が入力音声特徴ベクトルの数に比べて少なく、固定長でないような出力を表現できる。
前進・後退法(forward backward method)
正解文字列を順番に生成する確率を求める。
コスト関数:全パスの生起確率の負の対数尤度