背景
- これまでいろいろとコードを書き散らしてきたけど、まじめにテストができていなかったケースが多い
- テストのフレームワークはいろいろ聞いたことはあったけど実際に使ってみたことがなかった
- CIにも興味はあったが昔仕事でJenkinsを使ったくらいで、あまり有効活用できていなかった
- 両親がよく数独をやっているのと、旅行先の欧州によく数独本が売っていて、パズル解くアルゴリズムに興味があった
やりたいこと
- 数独を解くプログラムをC++で実装してみる
- 今更ながらGoogle Testを使った簡単な単体テストを作ってみる
- 最近GitHubでGitHub ActionsというCI向けの機能が無料化されたらしいので、使ってみる
- C++で書いた数独の解法アルゴリズムを、Google Testでテストする
- GitHubに上げて、GitHub ActionsからGoogle Testを叩いて自動テストする
数独ソルバー
まずは本体となる、数独を解くプログラムの実装から
アルゴリズム
検索してたらたどり着いた、DeepGreen's Computer Puzzle Solutionを
参考にさせていただきました。以下の解法はほぼこのサイトの記事の引用です。
今回の実装で用いる「次の一手を見つけるアルゴリズム」は、
- 探索的アルゴリズム
- シンプル法
- Enclosure法
- 背理法
の3つに分類できる。(実際にはシンプル法はEnclosure法の一部だが、高速化のため独立させている)
まず事前準備として以下のデータ構造を用意する。
- 確定盤面テーブル
- 9x9の盤面で、各マスは「未確定」または「確定」の状態を持つ
- 「確定」の場合は、確定した1~9いずれかの数字を保持している。
- 盤面が「合法である」とは、すべての確定済みのマスの「利きマス」に、当該確定済みマスと同じ数字が入らない状態をいう。
- ここで「利きマス」とは行、列、ブロックのいずれかで確定済みのマスと同じ組に入るマスのこと。
「次の一手」の探索とは、「未確定マスを含む、合法な確定盤面テーブル」を入力として受け取って、
「入力テーブルから一つの未確定マスが確定になった合法な確定盤面テーブル」を出力する操作と定義することができる。
また補助データ構造として以下のデータ構造も用意する。
- 候補テーブル
- 9x9の盤面で、各マスには「そのマスに入る可能性のある数字」をリストとして保持している。
- 確定盤面テーブルですでに確定済みのマスには候補リストは定義されない
シンプル法
シンプル法は単純で、確定盤面テーブルから候補テーブルを生成し、候補となる数字の数が0または1のマスを探索する。候補数が0のマスがあれば矛盾なので解なしで終了、候補数が1のマスがあればそのマスに入る数字が確定するので探索終了となる。
アルゴリズムは以下の通り:
- 確定盤面テーブルから候補テーブルを生成する。
2. すべてのマスに「1~9(すべての数字)」が候補リストとして埋まった候補テーブルを生成する
3. 確定盤面テーブルを走査し、候補テーブルから確定済みの数字の「利きマス」に相当するマスを辿っていって、候補リストから落とす。 - 候補テーブルが完成したら、候補テーブルを走査する
5. 候補数が0のマスがあれば解なしで終了
6. 候補数が1のマスがあればその候補を解として終了
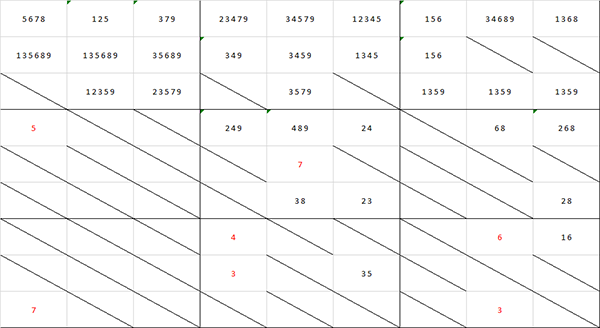
例
左上の4とその利きマスを候補から落とした状態(赤は利きマス)
生成された候補テーブルから、いくつかのマスが候補数1であり、確定可能であることがわかる(赤くしたマス)
Enclosure法
まず、数独における「タップル」を定義する。
タップルとは、「盤面が合法であるために同じ数字が確定してはいけない9個のマスのグループ」、
つまり「縦一列」or「横一列」or「3x3のブロック」に含まれる9個のマスのグループを指す。
n=1~9としたとき、候補テーブルから任意に選んだタップルに対し、Enclosure(n)という状態を定義する。
Enclosure(n)が成立するとは、
・選んだタップル内の任意のn個のマスに注目する
・n個のマスに保持されているすべての候補数字のORを取り、結果の候補数をmとする
・n=mだった場合、当該タップルとn個のマスに対してEnclosure(n)が成立。
Enclosure(n)が成立した場合、選ばれなかった9-n個のマスにはORを取った候補数字は入らなないことがわかるので、
これらのマスから候補数字を消してもよい。
さらに、Enclosure(n)を探索していく過程で一つでもm<nとなるタップルとマスの組み合わせが存在した場合、
その盤面は解なしであることがわかるので探索を打ち切ってよい。
つまり、ある盤面と候補テーブルが与えられたとき、Enclosure(n)を総当たりで探索し、
- m<nの組み合わせが見つかれば解なしで終了
- m=nの組み合わせが見つかれば候補テーブルを更新し、
- 候補数が0または1になるマスがあればシンプル法により解が一つ決定、あるいは解なしが確定
- 候補数が0または1になるマスが無ければ更新された候補テーブルに対してまた
Enclosure(n)の探索を開始
を繰り返すことで解を探すのがEnclosure法である。
例
候補テーブルから以下のようなタップルを選び出したとする(横一列のタップルに見えるが、縦でもボックスでもよい)

ここで左から3番目、4番目、7番目のマスに注目する。
これらのマスの候補数字は2 3 4 3 4 2 4なので、ORを取ると2 3 4。結果の候補数は3となる。
選んだマスの数3と一致するので、このタップルは3,4,7のマスに対してEnclosure(3)が成立しているといえる。
パズルの解法的に考えると、2 3 4の3つの数字は3,4,7の3つのマスにちょうど収まるので、それ以外のマスには入らない。
仮にm<nだった場合、n個のマスに対して入る数字がm個しかないので矛盾、すなわちその盤面は解なしになる。
Enclosure(3)が成立したので、残りの1,2,5,6,8,9のマスからは2 3 4の候補を消してもよい。
となり、8のマスでは候補数が1になるのでシンプル法により6が確定する。
実装を簡単にするため分けているが、実際はシンプル法はEnclosure(1)と同じである。
また、机上で数独を解くときによく使われる、「タップル内で特定の数字が1か所にしか入らない場合、その数字で確定」というテクニックはEnclosure(8)と同じであることもわかる。
背理法
「あるマスに数字nが入らないと仮定すると矛盾が生じるので、そのマスはnが入る」という論法。
- 候補テーブル内の任意のマスを選ぶ
- 選んだマスの候補リストから、任意の数字aを消す
- 消した結果の候補テーブルにシンプル法、Enclosure法を適用し、「解なし」という結果が得られるかどうかを探索する
- 「解なし」が得られた場合、選んだマスの数字はaで確定
- 「解なし」が得られなかった場合、aとは違う数字を選んで2.に戻る
- 候補リストのすべての数字を消しても「解なし」が得られなかった場合、1.に戻って違うマスを選んで繰り返す
引用元のページでは、
「すべての(解答可能な)数独問題は、Enclosure法と背理法の組み合わせで解くことができる」という仮説を立てている。
今回の実装でも試しにいくつかの高難易度の問題を与えてみたが、今のところ解けない問題には当たっていない。
実装
ソース https://github.com/y-uehara/SudokuLehrer
構成
後でGUIもつけてアプリケーション化したいが、テストしやすくするためまずはC++でバックエンドのみ実装することにする。
データ構造
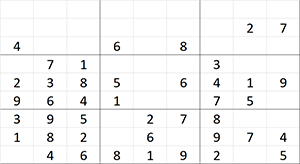
盤面データはシンプルにint型の配列で保持する。0は未確定マス。
盤面の例
int board[81] =
{8,9,0, 1,0,0, 0,0,5,
3,5,0, 9,0,0, 4,1,0,
1,0,0, 6,5,3, 0,0,9,
9,0,4, 3,0,8, 1,5,0,
0,0,5, 4,0,7, 0,6,0,
0,3,1, 0,0,5, 8,4,0,
0,0,0, 0,3,6, 0,0,1,
5,6,0, 0,4,0, 2,9,0,
7,1,8, 0,2,9, 0,0,0};
候補テーブルもシンプルにint型の配列で保持し、候補リストは数字を表すビットのORを取って表現する。
// 1: 0x001
// 2: 0x002
// 3: 0x004
// 4: 0x008
// 5: 0x010
// 6: 0x020
// 7: 0x040
// 8: 0x080
// 9: 0x100
// 1 2 3 4 5 6 6 7 8: 0x1ff
solve()関数
SudokuSolverResult solve(int *board);
解答アルゴリズムのエントリポイントとなる関数。テストを簡単にするため内部状態は持たず参照透過性を保持。
戻り値は探索の結果と、解が見つかった場合はその解をまとめて返す。
enum ResultType
{
FOUND,
NOT_FOUND,
CONTRADICT
};
struct SudokuSolverResult
{
ResultType result;
int x;
int y;
int num;
};
シンプル法
特に変わったことはせずに、力任せに実装。
SudokuSolver::SudokuSolverResult SudokuSolver::solve_simple(const int *board, int *candidates)
{
SudokuSolverResult ret;
for(int i = 0; i < 9; i++)
{
for(int j = 0; j < 9; j++)
{
if(board[9 * j + i] == 0)
{
// no candidate - contradict
if(candidates[9 * j + i] == 0)
{
ret.result = ResultType::CONTRADICT;
ret.x = ret.y = ret.num = -1;
return ret;
}
for(int k = 0; k < 9; k++)
{
if(candidates[9 * j + i] == (1 << k))
{
// found
ret.result = ResultType::FOUND;
ret.x = i;
ret.y = j;
ret.num = k+1;
return ret;
}
}
}
}
}
ret.result = ResultType::NOT_FOUND;
ret.x = -1;
ret.y = -1;
ret.num = -1;
return ret;
}
Enclosure法
まず、n=1~8の各nに対して、「タップル内の9マスからnマスを選ぶ組み合わせ」をすべて列挙する関数を定義する。
int SudokuSolver::createCombinationArray(int **array, unsigned int n, unsigned int r)
{
int combination = 1;
for(unsigned int i = 0; i < r; i++)
{
combination *= n-i;
}
for(unsigned int i = 0; i < r; i++)
{
combination = combination / (i+1);
}
*array = new int[combination];
int iter = 0;
unsigned int count;
for(unsigned int i = 0; i < std::pow(2, n); i++)
{
count = 0;
unsigned int mask = 0x1;
for(unsigned int j = 0; j < n; j++)
{
if((i&mask) != 0)
count++;
mask = mask << 1;
}
if(count == r)
{
(*array)[iter] = i;
iter++;
}
}
return combination;
}
候補テーブルからすべてのタップルを抽出し、n=1~8のすべての組み合わせに対してEnclosure(n)が成立しているかを計算し、成立していれば候補テーブルから該当するビットを落とす。
すべての組み合わせに対してEnclosure(n)の処理が終わったら、シンプル法を適用して確定できるマスがあるかどうかを判定する。
SudokuSolver::SudokuSolverResult SudokuSolver::solve_heuristic(const int *board, int *candidates)
{
int *combi = nullptr;
for(int n = 8; n > 0; n--)
{
// create bit array of 9Cn
createCombinationArray(&combi, 9, n);
for(int i = 0; i < 9; i++)
{
if(!solve_heuristic_iter(candidates, n, combi))
{
// contradict found
delete [] combi;
SudokuSolver::SudokuSolverResult ret;
ret.result = ResultType::CONTRADICT;
ret.x = ret.y = ret.num = -1;
return ret;
}
}
delete [] combi;
}
return solve_simple(board, candidates);
}
bool SudokuSolver::solve_heuristic_iter(int *candidates, int combiLength, int *combi)
{
for(auto tuple : SudokuTuples)
{
int cover = 0;
for(int i = 0; i < 9; i++)
{
if(combi[i] & (0x1 << i))
cover |= candidates[tuple[i]];
}
// count num of 1
int bits = 0;
int mask = 0;
for(int k = 0; k < 9; k++)
{
// count bit and create mask
if(cover & (0x1 << k))
{
bits++;
mask |= 0x1 << k;
}
}
if(bits == combiLength)
{
// apply mask to remaining elements
for(int i = 0; i < 9; i++)
{
if(!(combi[i] & (0x1 << i)))
candidates[tuple[i]] &= ~mask;
}
}
else if(bits < combiLength)
{
// contradict
return false;
}
}
return true;
}
背理法
候補リストが少ないマスのほうが処理が早いので、候補数が2のマスから順に処理する。
該当マスの候補リストの中から任意の1つを落とした候補テーブルを作成し、シンプル法+Enclosure法で解の探索を行う。
最終的に矛盾=解なしが導ければ最初に落とした数字を解として返す。
矛盾が導けなければ、他の数字を落として繰り返す。
SudokuSolver::SudokuSolverResult SudokuSolver::solve_negation(const int *board, int *candidates)
{
SudokuSolverResult ret;
// keep candidates
int *work_board = new int[9*9];
int *work_candidates = new int[9*9];
std::vector<int> assumption;
// search item with n candidates
for(unsigned int n = 2; n <= 9; n++)
{
for(int i = 0; i < 9*9; i++)
{
assumption.clear();
for(unsigned int j = 0; j < 9; j++)
{
if((candidates[i] & (0x1 << j)) != 0)
{
assumption.push_back(j);
}
}
if(assumption.size() == n)
{
for(unsigned int j = 0; j < n; j++)
{
//printf("try to negation...[%d %d] as %d\n", i%9, i/9, assumption[j]+1);
memcpy(work_board, board, sizeof(int) * 9 * 9);
memcpy(work_candidates, candidates, sizeof(int) * 9 * 9);
unsigned int mask = (0x1 << assumption[j]);
work_candidates[i] &= ~mask;
while(true)
{
ret = solve_simple(work_board, work_candidates);
if(ret.result == ResultType::FOUND)
{
work_board[9*ret.y+ret.x] = ret.num;
removeCandidate(ret.num, std::make_pair(ret.x, ret.y), work_candidates);
continue;
}
else if(ret.result == ResultType::CONTRADICT)
{
break;
}
ret = solve_heuristic(work_board, work_candidates);
if(ret.result == ResultType::FOUND)
{
work_board[9*ret.y+ret.x] = ret.num;
removeCandidate(ret.num, std::make_pair(ret.x, ret.y), work_candidates);
continue;
}
else
{
break;
}
}
if(ret.result == ResultType::CONTRADICT)
{
//printf("contradict found. [%d %d] can be guessed to %d\n", i%9, i/9, assumption[j]+1);
ret.result = ResultType::FOUND;
ret.x = i % 9;
ret.y = i / 9;
ret.num = assumption[j]+1;
delete [] work_board;
delete [] work_candidates;
return ret;
}
}
}
}
}
ret.result = ResultType::NOT_FOUND;
ret.x = -1;
ret.y = -1;
ret.num = -1;
delete [] work_board;
delete [] work_candidates;
return ret;
}
Google Testで単体テストする
以上の数独アルゴリズムを簡単にテストすることを考える。
C++用の単体テストフレームワークは簡単に調べた限りでもいろいろあって
- Boost.Test
- Google Test
- CppUnit
などがあるが、今回はGoogle Testを試しに使ってみることにする。
一定条件を満たしたテストフレームワークのことをxUnitと総称するらしい → https://ja.wikipedia.org/wiki/XUnit
入門ガイド(なぜかOpenCVのページにある) → http://opencv.jp/googletestdocs/primer.html
Google Testライブラリのビルドとリンク
Google TestのソースをGithubから落としてきてcmake+Visual Studioでビルドすると、以下のライブラリができる。
- gtest.lib, gtest_main.lib, gmock.lib, gmock_main.lib
- gtest.pdb, gtest_main.pdb, gmock.pdb, gmock_main.pdb (デバッガシンボルファイル)
これらのライブラリをテストコードにリンクすればいいはず。
Debianではaptでインストールできる
# apt install libgtest-dev
が、将来的にCIでテストすることを考えるとGoogle Testのライブラリをローカルに用意するのはいまいちで、
Googleさんが推奨 https://github.com/google/googletest/blob/master/googletest/README.md している通り、
GoogleTest自体をCMakeのビルド工程で毎回ダウンロードしてきてビルドするやり方がよさそう。
上記ページを参考にCMakeLists.txt.inとCMakeLists.txtを作成して、testフォルダ以下に配置する。
CMakeLists.txtの以下の部分をテストしたいプロジェクトに合わせて書き換えればよい。
# Now simply link against gtest or gtest_main as needed. Eg
add_executable(example example.cpp)
target_link_libraries(example gtest_main)
add_test(NAME example_test COMMAND example)
この準備をしてcmakeを叩くと、自動的にGoogle Testの最新リポジトリをダウンロードしてきてビルドまで行ってくれる。テストの実行環境によってGoogle Testが入っていなかったりバージョンが違って動作が異なったりするトラブルを避けるためには、このようにテスト対象のリポジトリにテストツールまで含めてしまうやり方が結局スムーズなのかもしれない。
Google Testを使ったテストコードの実装
Google Testの基本構造は以下のような感じ
# include "gtest/gtest.h"
TEST(TestCategoly TestCase)
{
ASSERT_XX();
EXPECT_XX();
}
TEST()マクロでテストケースを定義し、テストケース内にASSERT_XX()やEXPECT_XX()マクロを書いてアサーション条件を定義する。テストコード自体はC++で普通に書けばよい。
パラメータ化したテストケースも簡単に作れるようだ
まず列挙子?のクラスを定義、これはフィクスタも継承しているのでTearUpとかも書ける
class <class> : public ::testing::TestWithParam<int> { };
テストケースのテンプレを定義しておいて、
TEST_P(<class>, <test_case_name>)
{
int i = GetParam();
ASSERT_XX();
}
インスタンス化する。
INSTANTIATE_TEST_CASE_P(<test_categoly>, <class>, ::testing::Range(0,2));
これでテスト対象データを順次変えながらのテスト実行などをシンプルに書くことができる。
上記の例ではGetParam()の戻り値が0-2のテストケースが自動的に生成される。
数独アルゴリズムをテストするコードは以下のような感じになる。
アサーション条件は以下の通り。
- 確定マスが81未満で合法な盤面を与えて
solve()関数を呼ぶと、「次の一手」が返ってくる - 「次の一手」を反映させた盤面もまた合法である
- 「次の一手」を反映させると、確定マスが反映前より増えている(パズルが進んでいる)
以上の条件を満たした結果が得られたら、テストは成功とする。
今回の実装ではsolve()関数は参照透過性があるのでテスト結果は引数のみに依存。
# include <iostream>
# include <set>
# include <vector>
# include <gtest/gtest.h>
# include "../sudokusolver.h"
const int SudokuTuples[27][9] =
{
// columns
{ 0, 1, 2, 3, 4, 5, 6, 7, 8},
{ 9, 10, 11, 12, 13, 14, 15, 16, 17},
{18, 19, 20, 21, 22, 23, 24, 25, 26},
{27, 28, 29, 30, 31, 32, 33, 34, 35},
{36, 37, 38, 39, 40, 41, 42, 43, 44},
{45, 46, 47, 48, 49, 50, 51, 52, 53},
{54, 55, 56, 57, 58, 59, 60, 61, 62},
{63, 64, 65, 66, 67, 68, 69, 70, 71},
{72, 73, 74, 75, 76, 77, 78, 79, 80},
// rows
{ 0, 9, 18, 27, 36, 45, 54, 63, 72},
{ 1, 10, 19, 28, 37, 46, 55, 64, 73},
{ 2, 11, 20, 29, 38, 47, 56, 65, 74},
{ 3, 12, 21, 30, 39, 48, 57, 66, 75},
{ 4, 13, 22, 31, 40, 49, 58, 67, 76},
{ 5, 14, 23, 32, 41, 50, 59, 68, 77},
{ 6, 15, 24, 33, 42, 51, 60, 69, 78},
{ 7, 16, 25, 34, 43, 52, 61, 70, 79},
{ 8, 17, 26, 35, 44, 53, 62, 71, 80},
// boxes
{ 0, 1, 2, 9, 10, 11, 18, 19, 20},
{ 3, 4, 5, 12, 13, 14, 21, 22, 23},
{ 6, 7, 8, 15, 16, 17, 24, 25, 26},
{27, 28, 29, 36, 37, 38, 45, 46, 47},
{30, 31, 32, 39, 40, 41, 48, 49, 50},
{33, 34, 35, 42, 43, 44, 51, 52, 53},
{54, 55, 56, 63, 64, 65, 72, 73, 74},
{57, 58, 59, 66, 67, 68, 75, 76, 77},
{60, 61, 62, 69, 70, 71, 78, 79, 80}
};
# include "sudokusolver-testCase.cpp"
bool check_legal_tuple(std::vector<int> tuple)
{
int count = 0;
std::set<int> numSet;
//printf("check tuple [%d %d %d %d %d %d %d %d %d]\n",
// tuple[0],tuple[1],tuple[2],tuple[3],tuple[4],tuple[5],tuple[6],tuple[7],tuple[8]);
for(unsigned int i = 0; i < tuple.size(); i++)
{
if(tuple[i] != 0)
{
count++;
numSet.insert(tuple[i]);
}
}
return (numSet.size() == count);
}
bool check_legal_board(int *board)
{
std::vector<int> tuple;
for(int i = 0; i < 27; i++)
{
tuple.clear();
for(int j = 0; j < 9; j++)
tuple.push_back(board[SudokuTuples[i][j]]);
if(!check_legal_tuple(tuple))
return false;
}
return true;
}
int count_fixed(int *board)
{
int fixed = 0;
for(int i = 0; i < 81; i++)
{
if(board[i] != 0)
fixed++;
}
return fixed;
}
void dump(int *board)
{
for(int i = 0; i < 9; i++)
{
for(int j = 0; j < 9; j++)
{
std::cout << board[9*i + j] << " ";
if(j % 3 == 2)
std::cout << " ";
}
std::cout << std::endl;
if(i % 3 == 2)
std::cout << std::endl;
}
}
class QuizList : public ::testing::TestWithParam<int> { };
TEST_P(QuizList, ResultTest)
{
int i = GetParam();
auto solver = new SudokuSolver();
SudokuSolver::SudokuSolverResult result;
int count_before, count_after;
while(81 > count_fixed(test_case[i]))
{
//printf("count fixed:%d\n",count_fixed(test_case[i]));
result = solver->solve(test_case[i]);
//printf("ret:%s, x:%d y:%d num:%d\n", (result.result == SudokuSolver::ResultType::FOUND ? "FOUND" : (result.result == SudokuSolver::ResultType::NOT_FOUND ? "NOT FOUND" : "CONTRADICT")), result.x, result.y, result.num);
// answer not found
if(result.result != SudokuSolver::ResultType::FOUND)
{
// show final board status
dump(test_case[i]);
}
ASSERT_TRUE(result.result == SudokuSolver::ResultType::FOUND);
// apply change
count_before = count_fixed(test_case[i]);
//printf("counter before:%d\n", count_before);
test_case[i][9*result.y + result.x] = result.num;
count_after = count_fixed(test_case[i]);
//printf("counter after:%d\n", count_after);
// increase fixed number
ASSERT_GT(count_after, count_before);
// answer is legal
//printf("legal check\n");
ASSERT_TRUE(check_legal_board(test_case[i]));
//printf("answer is legal\n");
}
}
# define NUM_OF_TEST_CASE (static_cast<int>((sizeof(test_case) / sizeof(test_case[0]))))
INSTANTIATE_TEST_CASE_P(SudokuSolverTest, QuizList, ::testing::Range(0, NUM_OF_TEST_CASE));
テストケースは別ファイルで与える。
int test_case[][81] =
{
// easy
{8,9,0, 1,0,0, 0,0,5,
3,5,0, 9,0,0, 4,1,0,
1,0,0, 6,5,3, 0,0,9,
9,0,4, 3,0,8, 1,5,0,
0,0,5, 4,0,7, 0,6,0,
0,3,1, 0,0,5, 8,4,0,
0,0,0, 0,3,6, 0,0,1,
5,6,0, 0,4,0, 2,9,0,
7,1,8, 0,2,9, 0,0,0},
// ...
// super difficult
{0,0,0, 0,0,0, 4,0,0,
2,0,0, 0,9,6, 1,3,0,
0,8,0, 0,3,0, 0,0,0,
1,0,0, 0,0,0, 0,6,0,
0,0,2, 0,0,8, 0,0,0,
0,4,0, 3,2,5, 0,0,8,
0,0,0, 0,0,0, 0,5,0,
0,0,9, 0,0,2, 0,0,4,
0,0,0, 9,6,7, 0,0,0},
// ...
};
テストのビルドの実行は以下のようになる。(Visual Studioの場合。gccの場合は--config以下は不要)
# cd test
# mkdir build
# cd build
# cmake ..
# cmake --build . --config Release
実行結果。きちんとテストできている。
PS C:\git\SudokuLehrer\backend\test\build\Release> .\sudokusolver-test.exe
Running main() from C:\git\SudokuLehrer\backend\test\build\googletest-src\googletest\src\gtest_main.cc
[==========] Running 12 tests from 1 test suite.
[----------] Global test environment set-up.
[----------] 12 tests from SudokuSolverTest/QuizList
[ RUN ] SudokuSolverTest/QuizList.ResultTest/0
[ OK ] SudokuSolverTest/QuizList.ResultTest/0 (4 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/1
[ OK ] SudokuSolverTest/QuizList.ResultTest/1 (4 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/2
[ OK ] SudokuSolverTest/QuizList.ResultTest/2 (6 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/3
[ OK ] SudokuSolverTest/QuizList.ResultTest/3 (28 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/4
[ OK ] SudokuSolverTest/QuizList.ResultTest/4 (16 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/5
[ OK ] SudokuSolverTest/QuizList.ResultTest/5 (35 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/6
[ OK ] SudokuSolverTest/QuizList.ResultTest/6 (5 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/7
[ OK ] SudokuSolverTest/QuizList.ResultTest/7 (7 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/8
[ OK ] SudokuSolverTest/QuizList.ResultTest/8 (13 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/9
[ OK ] SudokuSolverTest/QuizList.ResultTest/9 (9 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/10
[ OK ] SudokuSolverTest/QuizList.ResultTest/10 (11 ms)
[ RUN ] SudokuSolverTest/QuizList.ResultTest/11
[ OK ] SudokuSolverTest/QuizList.ResultTest/11 (22 ms)
[----------] 12 tests from SudokuSolverTest/QuizList (173 ms total)
[----------] Global test environment tear-down
[==========] 12 tests from 1 test suite ran. (175 ms total)
[ PASSED ] 12 tests.
GitHub ActionsでCIする
設定
ローカルで実行できたGoogle Testのテストを、GitHub上でpushをトリガーに自動実行できるようにする。
最近GitHub Actionsという名前で無料でCIが使えるようになったので、試してみる
リポジトリトップの.github/workflows/ に *.yml ファイルを置けば自動的に実行される。(ファイル名はなんでもいい)
中身はこんな感じ
name: CI
on: [push]
jobs:
backend_test:
runs-on: ubuntu-latest
steps:
- uses: actions/checkout@v2
- name: create build directory
run: |
cd backend/test
mkdir build
- name: download GoogleTest and build test
run: |
cd backend/test/build
cmake ..
cmake --build .
- name: run test
run: backend/test/build/sudokusolver-test
GitHubさん提供のUbuntu仮想マシンを使って、以下の処理を順次行う。
- リポジトリになんらかのコードがpushされたら
- コードをチェックアウトする
- backend/test 以下に build/ ディレクトリを作成する
- cmakeを叩いて、Google Testのソースを公式リポジトリからダウンロード、ビルドする
実行結果
以上の設定をしておくと、GitHubのWeb UI上の「Actions」からテスト実行結果を見ることができようになる。
Actionsのリンクをクリックすると以下のような画面が見られる
こんな感じ(name: CI)
backend_test: は勝手につけたジョブの名前。実行結果に入っていくと以下のようになる
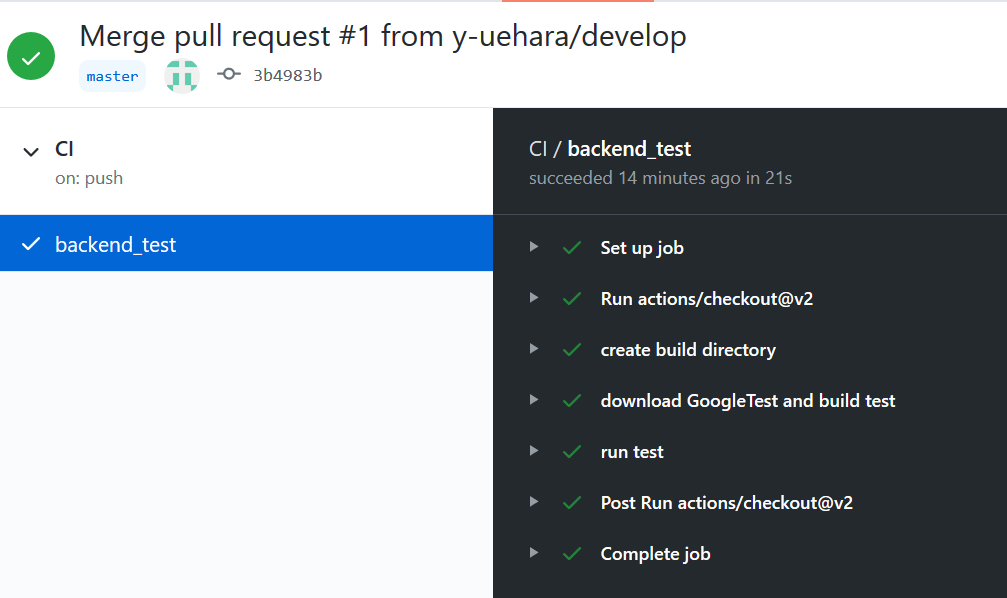
右のペインを開くと実行結果が細かく見られる。

ローカルで実行したときと同じ結果が得られている。
テストが失敗すると、メールで通知が飛んでくる模様。
Topic
-
pushはブランチ指定とかもできる模様。上の例ではすべてのブランチに対して有効 -
jobsに並べたジョブはすべて並行実行される -
steps:に書いたコマンドは順次実行 -
uses:はGitHubさんが用意したスクリプトを使う書き方。checkout@v2は何かバージョンアップしたらしい -
run:は一行にまとめて書かないと別プロセスになるため、カレントディレクトリなどが保持されない - カレントディレクトリを変えたりしながら一連のコマンドを実行するには
|を使って複数行runを使う必要あり - 標準出力を見たいときは逆に
run:を一行にしないとうまくGUI上には表示されない模様 - GoogleTestを使って作ったテストプログラムはちゃんと成功/失敗を返してくれる(プロセスの返り値)模様。かしこい
今後の展開
- 今回作った数独アルゴリズムにQtでGUIをつける
- カメラで撮った問題画像を認識してそこから解答できるようにする
- Android+Qtで動かす